Closest Nodes Queries in a Binary Search Tree
MediumUpdated: Jul 7, 2025
Practice on:
Problem
You are given the root of a binary search tree and an array queries of size n consisting of positive integers.
Find a 2D array answer of size n where answer[i] = [mini, maxi]:
miniis the largest value in the tree that is smaller than or equal toqueries[i]. If a such value does not exist, add-1instead.maxiis the smallest value in the tree that is greater than or equal toqueries[i]. If a such value does not exist, add-1instead.
Return the array answer.
Examples
Example 1
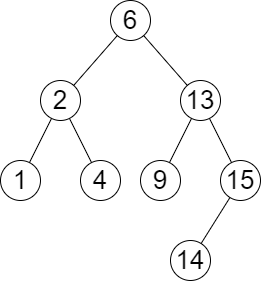
Input: root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
Output: [[2,2],[4,6],[15,-1]]
Explanation: We answer the queries in the following way:
- The largest number that is smaller or equal than 2 in the tree is 2, and the smallest number that is greater or equal than 2 is still 2. So the answer for the first query is [2,2].
- The largest number that is smaller or equal than 5 in the tree is 4, and the smallest number that is greater or equal than 5 is 6. So the answer for the second query is [4,6].
- The largest number that is smaller or equal than 16 in the tree is 15, and the smallest number that is greater or equal than 16 does not exist. So the answer for the third query is [15,-1].
Example 2
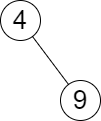
Input: root = [4,null,9], queries = [3]
Output: [[-1,4]]
Explanation: The largest number that is smaller or equal to 3 in the tree does not exist, and the smallest number that is greater or equal to 3 is 4. So the answer for the query is [-1,4].
Constraints
- The number of nodes in the tree is in the range
[2, 105]. 1 <= Node.val <= 10^6n == queries.length1 <= n <= 10^51 <= queries[i] <= 10^6
Solution
Method 1 – Inorder Traversal + Binary Search
Intuition
A binary search tree's inorder traversal yields a sorted list of values. For each query, we can use binary search on this sorted list to efficiently find the largest value ≤ query and the smallest value ≥ query.
Approach
- Traverse the BST in inorder to collect all values in a sorted array.
- For each query:
- Use binary search to find the rightmost value ≤ query (for mini).
- Use binary search to find the leftmost value ≥ query (for maxi).
- If such values do not exist, use -1.
- Return the answer for all queries.
Code
C++
class Solution {
public:
void inorder(TreeNode* root, vector<int>& vals) {
if (!root) return;
inorder(root->left, vals);
vals.push_back(root->val);
inorder(root->right, vals);
}
vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {
vector<int> vals;
inorder(root, vals);
vector<vector<int>> ans;
for (int q : queries) {
auto it1 = upper_bound(vals.begin(), vals.end(), q);
int mini = (it1 == vals.begin()) ? -1 : *(--it1);
auto it2 = lower_bound(vals.begin(), vals.end(), q);
int maxi = (it2 == vals.end()) ? -1 : *it2;
ans.push_back({mini, maxi});
}
return ans;
}
};
Go
type TreeNode struct {
Val int
Left, Right *TreeNode
}
func closestNodes(root *TreeNode, queries []int) [][]int {
var vals []int
var inorder func(*TreeNode)
inorder = func(node *TreeNode) {
if node == nil { return }
inorder(node.Left)
vals = append(vals, node.Val)
inorder(node.Right)
}
inorder(root)
ans := make([][]int, len(queries))
for i, q := range queries {
mini, maxi := -1, -1
l, r := 0, len(vals)-1
for l <= r {
m := (l + r) / 2
if vals[m] <= q {
mini = vals[m]
l = m + 1
} else {
r = m - 1
}
}
l, r = 0, len(vals)-1
for l <= r {
m := (l + r) / 2
if vals[m] >= q {
maxi = vals[m]
r = m - 1
} else {
l = m + 1
}
}
ans[i] = []int{mini, maxi}
}
return ans
}
Java
class Solution {
List<Integer> vals = new ArrayList<>();
void inorder(TreeNode root) {
if (root == null) return;
inorder(root.left);
vals.add(root.val);
inorder(root.right);
}
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
inorder(root);
List<List<Integer>> ans = new ArrayList<>();
for (int q : queries) {
int mini = -1, maxi = -1;
int l = 0, r = vals.size() - 1;
while (l <= r) {
int m = (l + r) / 2;
if (vals.get(m) <= q) {
mini = vals.get(m);
l = m + 1;
} else {
r = m - 1;
}
}
l = 0; r = vals.size() - 1;
while (l <= r) {
int m = (l + r) / 2;
if (vals.get(m) >= q) {
maxi = vals.get(m);
r = m - 1;
} else {
l = m + 1;
}
}
ans.add(Arrays.asList(mini, maxi));
}
return ans;
}
}
Kotlin
class Solution {
fun closestNodes(root: TreeNode?, queries: List<Int>): List<List<Int>> {
val vals = mutableListOf<Int>()
fun inorder(node: TreeNode?) {
if (node == null) return
inorder(node.left)
vals.add(node.`val`)
inorder(node.right)
}
inorder(root)
return queries.map { q ->
var mini = -1; var maxi = -1
var l = 0; var r = vals.size - 1
while (l <= r) {
val m = (l + r) / 2
if (vals[m] <= q) { mini = vals[m]; l = m + 1 } else { r = m - 1 }
}
l = 0; r = vals.size - 1
while (l <= r) {
val m = (l + r) / 2
if (vals[m] >= q) { maxi = vals[m]; r = m - 1 } else { l = m + 1 }
}
listOf(mini, maxi)
}
}
}
Python
class Solution:
def closestNodes(self, root: 'TreeNode', queries: list[int]) -> list[list[int]]:
vals = []
def inorder(node):
if not node: return
inorder(node.left)
vals.append(node.val)
inorder(node.right)
inorder(root)
ans = []
for q in queries:
mini, maxi = -1, -1
l, r = 0, len(vals) - 1
while l <= r:
m = (l + r) // 2
if vals[m] <= q:
mini = vals[m]
l = m + 1
else:
r = m - 1
l, r = 0, len(vals) - 1
while l <= r:
m = (l + r) // 2
if vals[m] >= q:
maxi = vals[m]
r = m - 1
else:
l = m + 1
ans.append([mini, maxi])
return ans
Rust
impl Solution {
pub fn closest_nodes(root: Option<Rc<RefCell<TreeNode>>>, queries: Vec<i32>) -> Vec<Vec<i32>> {
fn inorder(node: Option<Rc<RefCell<TreeNode>>>, vals: &mut Vec<i32>) {
if let Some(n) = node {
inorder(n.borrow().left.clone(), vals);
vals.push(n.borrow().val);
inorder(n.borrow().right.clone(), vals);
}
}
let mut vals = vec![];
inorder(root, &mut vals);
let mut ans = vec![];
for q in queries {
let (mut mini, mut maxi) = (-1, -1);
let (mut l, mut r) = (0, vals.len() as i32 - 1);
while l <= r {
let m = (l + r) / 2;
if vals[m as usize] <= q {
mini = vals[m as usize];
l = m + 1;
} else {
r = m - 1;
}
}
l = 0; r = vals.len() as i32 - 1;
while l <= r {
let m = (l + r) / 2;
if vals[m as usize] >= q {
maxi = vals[m as usize];
r = m - 1;
} else {
l = m + 1;
}
}
ans.push(vec![mini, maxi]);
}
ans
}
}
TypeScript
class Solution {
closestNodes(root: TreeNode | null, queries: number[]): number[][] {
const vals: number[] = [];
function inorder(node: TreeNode | null) {
if (!node) return;
inorder(node.left);
vals.push(node.val);
inorder(node.right);
}
inorder(root);
return queries.map(q => {
let mini = -1, maxi = -1;
let l = 0, r = vals.length - 1;
while (l <= r) {
const m = (l + r) >> 1;
if (vals[m] <= q) { mini = vals[m]; l = m + 1; } else { r = m - 1; }
}
l = 0; r = vals.length - 1;
while (l <= r) {
const m = (l + r) >> 1;
if (vals[m] >= q) { maxi = vals[m]; r = m - 1; } else { l = m + 1; }
}
return [mini, maxi];
});
}
}
Complexity
- ⏰ Time complexity: O(n + q log n), where n is the number of nodes and q is the number of queries.
- 🧺 Space complexity: O(n)