Collect Coins in a Tree
Problem
There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given an integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an array coins of size n where coins[i] can be either 0 or 1, where 1 indicates the presence of a coin in the vertex i.
Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times:
- Collect all the coins that are at a distance of at most
2from the current vertex, or - Move to any adjacent vertex in the tree.
Find the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex.
Note that if you pass an edge several times, you need to count it into the answer several times.
Examples
Example 1
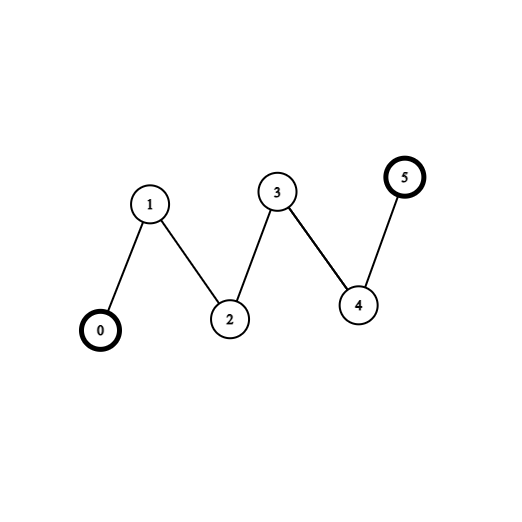
Input: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
Output: 2
Explanation: Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.
Example 2
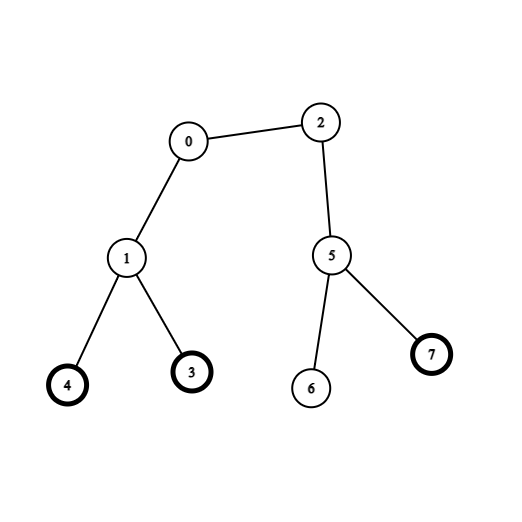
Input: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
Output: 2
Explanation: Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2, collect the coin at vertex 7, then move back to vertex 0.
Constraints
n == coins.length1 <= n <= 3 * 10^40 <= coins[i] <= 1edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedgesrepresents a valid tree.
Solution
Method 1 – Prune Leaves and BFS
Intuition
We can prune all leaves that do not have coins, as they are not needed for collection. After pruning, the minimum number of edges to traverse is twice the number of remaining edges minus the ability to start and end within distance 2 of all coins (so we can avoid traversing the outermost two layers).
Approach
- Build the tree as an adjacency list.
- Prune all leaves without coins by repeatedly removing them and updating their neighbors.
- After pruning, perform two rounds of leaf removal (BFS) to simulate the ability to collect coins within distance 2.
- The answer is the number of remaining edges times 2 (since each edge is traversed twice).
Code
C++
class Solution {
public:
int collectTheCoins(vector<int>& coins, vector<vector<int>>& edges) {
int n = coins.size();
vector<vector<int>> g(n);
vector<int> deg(n);
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
deg[e[0]]++;
deg[e[1]]++;
}
queue<int> q;
for (int i = 0; i < n; ++i) if (deg[i] == 1 && coins[i] == 0) q.push(i);
int rem = n;
while (!q.empty()) {
int u = q.front(); q.pop(); rem--;
for (int v : g[u]) if (--deg[v] == 1 && coins[v] == 0) q.push(v);
}
for (int t = 0; t < 2; ++t) {
for (int i = 0; i < n; ++i) if (deg[i] == 1) q.push(i);
int sz = q.size();
while (sz--) {
int u = q.front(); q.pop(); rem--;
for (int v : g[u]) if (--deg[v] == 1) q.push(v);
}
}
return rem <= 1 ? 0 : (rem - 1) * 2;
}
};
Go
func collectTheCoins(coins []int, edges [][]int) int {
n := len(coins)
g := make([][]int, n)
deg := make([]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], e[1])
g[e[1]] = append(g[e[1]], e[0])
deg[e[0]]++
deg[e[1]]++
}
q := []int{}
for i := 0; i < n; i++ {
if deg[i] == 1 && coins[i] == 0 {
q = append(q, i)
}
}
rem := n
for len(q) > 0 {
u := q[0]; q = q[1:]; rem--
for _, v := range g[u] {
deg[v]--
if deg[v] == 1 && coins[v] == 0 {
q = append(q, v)
}
}
}
for t := 0; t < 2; t++ {
nq := []int{}
for i := 0; i < n; i++ {
if deg[i] == 1 {
nq = append(nq, i)
}
}
for _, u := range nq {
rem--
for _, v := range g[u] {
deg[v]--
}
}
}
if rem <= 1 {
return 0
}
return (rem - 1) * 2
}
Java
class Solution {
public int collectTheCoins(int[] coins, int[][] edges) {
int n = coins.length;
List<Integer>[] g = new ArrayList[n];
int[] deg = new int[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
deg[e[0]]++;
deg[e[1]]++;
}
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < n; i++) if (deg[i] == 1 && coins[i] == 0) q.add(i);
int rem = n;
while (!q.isEmpty()) {
int u = q.poll(); rem--;
for (int v : g[u]) if (--deg[v] == 1 && coins[v] == 0) q.add(v);
}
for (int t = 0; t < 2; t++) {
q = new LinkedList<>();
for (int i = 0; i < n; i++) if (deg[i] == 1) q.add(i);
int sz = q.size();
while (sz-- > 0) {
int u = q.poll(); rem--;
for (int v : g[u]) deg[v]--;
}
}
return rem <= 1 ? 0 : (rem - 1) * 2;
}
}
Kotlin
class Solution {
fun collectTheCoins(coins: IntArray, edges: Array<IntArray>): Int {
val n = coins.size
val g = Array(n) { mutableListOf<Int>() }
val deg = IntArray(n)
for (e in edges) {
g[e[0]].add(e[1])
g[e[1]].add(e[0])
deg[e[0]]++
deg[e[1]]++
}
val q = ArrayDeque<Int>()
for (i in 0 until n) if (deg[i] == 1 && coins[i] == 0) q.add(i)
var rem = n
while (q.isNotEmpty()) {
val u = q.removeFirst(); rem--
for (v in g[u]) if (--deg[v] == 1 && coins[v] == 0) q.add(v)
}
repeat(2) {
val nq = ArrayDeque<Int>()
for (i in 0 until n) if (deg[i] == 1) nq.add(i)
for (u in nq) {
rem--
for (v in g[u]) deg[v]--
}
}
return if (rem <= 1) 0 else (rem - 1) * 2
}
}
Python
class Solution:
def collectTheCoins(self, coins: list[int], edges: list[list[int]]) -> int:
n = len(coins)
g = [[] for _ in range(n)]
deg = [0] * n
for u, v in edges:
g[u].append(v)
g[v].append(u)
deg[u] += 1
deg[v] += 1
q = [i for i in range(n) if deg[i] == 1 and coins[i] == 0]
rem = n
while q:
u = q.pop()
rem -= 1
for v in g[u]:
deg[v] -= 1
if deg[v] == 1 and coins[v] == 0:
q.append(v)
for _ in range(2):
nq = [i for i in range(n) if deg[i] == 1]
for u in nq:
rem -= 1
for v in g[u]:
deg[v] -= 1
return 0 if rem <= 1 else (rem - 1) * 2
Rust
impl Solution {
pub fn collect_the_coins(coins: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
let n = coins.len();
let mut g = vec![vec![]; n];
let mut deg = vec![0; n];
for e in &edges {
g[e[0] as usize].push(e[1] as usize);
g[e[1] as usize].push(e[0] as usize);
deg[e[0] as usize] += 1;
deg[e[1] as usize] += 1;
}
let mut q = vec![];
for i in 0..n {
if deg[i] == 1 && coins[i] == 0 {
q.push(i);
}
}
let mut rem = n;
while let Some(u) = q.pop() {
rem -= 1;
for &v in &g[u] {
deg[v] -= 1;
if deg[v] == 1 && coins[v] == 0 {
q.push(v);
}
}
}
for _ in 0..2 {
let nq: Vec<_> = (0..n).filter(|&i| deg[i] == 1).collect();
for &u in &nq {
rem -= 1;
for &v in &g[u] {
deg[v] -= 1;
}
}
}
if rem <= 1 { 0 } else { ((rem - 1) * 2) as i32 }
}
}
TypeScript
class Solution {
collectTheCoins(coins: number[], edges: number[][]): number {
const n = coins.length;
const g: number[][] = Array.from({length: n}, () => []);
const deg: number[] = Array(n).fill(0);
for (const [u, v] of edges) {
g[u].push(v);
g[v].push(u);
deg[u]++;
deg[v]++;
}
let q: number[] = [];
for (let i = 0; i < n; i++) if (deg[i] === 1 && coins[i] === 0) q.push(i);
let rem = n;
while (q.length) {
const u = q.pop()!; rem--;
for (const v of g[u]) {
deg[v]--;
if (deg[v] === 1 && coins[v] === 0) q.push(v);
}
}
for (let t = 0; t < 2; t++) {
const nq: number[] = [];
for (let i = 0; i < n; i++) if (deg[i] === 1) nq.push(i);
for (const u of nq) {
rem--;
for (const v of g[u]) deg[v]--;
}
}
return rem <= 1 ? 0 : (rem - 1) * 2;
}
}
Complexity
- ⏰ Time complexity:
O(n) - 🧺 Space complexity:
O(n)