Combination Sum 1

Problem

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

It is guaranteed that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Examples

Example 1:

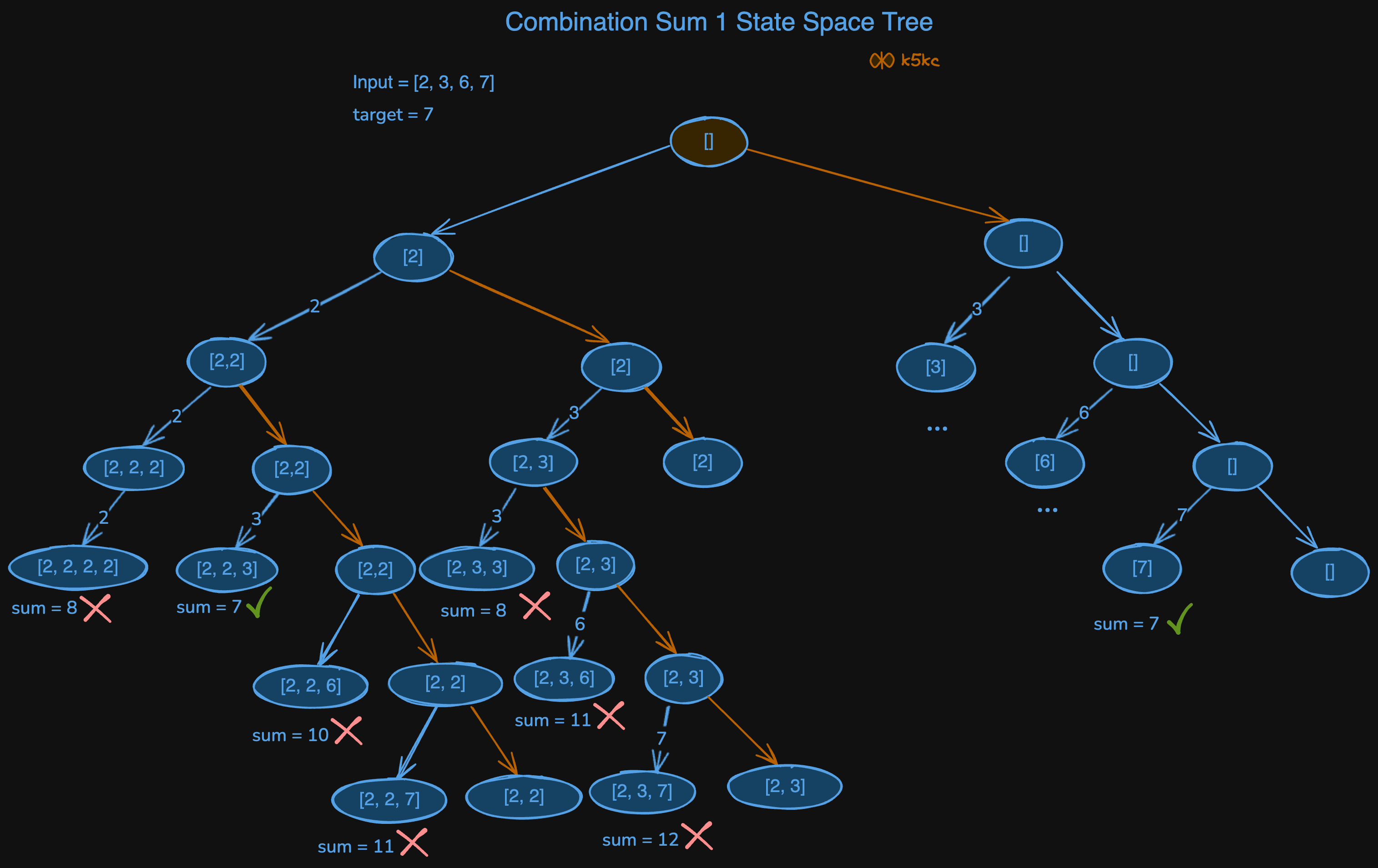
Input: candidates = [2,3,6,7], target = 7
Output:[[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

Input: candidates = [2,3,5], target = 8
Output:[[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

Constraints

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
All elements of candidates are distinct.
1 <= target <= 40

Note

- All numbers (including target) will be positive integers.
- Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
- The combinations themselves must be sorted in ascending order.
- CombinationA > CombinationB iff (a1 > b1) OR (a1 = b1 AND a2 > b2) OR … (a1 = b1 AND a2 = b2 AND … ai = bi AND ai+1 > bi+1)
- The solution set must not contain duplicate combinations.

Warning : DO NOT USE LIBRARY FUNCTION FOR GENERATING COMBINATIONS. Example : itertools.combinations in python.

Solution

Method 1 - Backtracking

The first impression of this problem should be depth-first search(DFS). To solve DFS problem, recursion is a normal implementation.

Note that the candidates array is not sorted, we need to sort it first, if we need sorted output from the list. But this is not necessary.

Backtracking the wrong way

Also, normal recursion decision tree may have issues. For e.g. for array [2,3,6,7], when we choose 2, it may have 3 later. So, when we come to number 3, we should make sure, that we don't take 2 again, as that will result in duplicates.

graph TD
    Root["[]"]
    Root --> A("[2]")
    Root --> B("[3]")
    Root --> C("[6]")
    Root --> D("[7]")

    A --> AA("[2, 2]")
    A --> AB("[2, 3]")
    A --> AC("[2, 6]")
    A --> AD("[2, 7]")
    B --> BA("[3, 2]")
    B --> BB("[3, 3]")
    B --> BC("[3, 6]")
    B --> BD("[3, 7]")
    C --> CA("[6, 2]")
    C --> CB("[6, 3]")
    C --> CC("[6, 6]")
    C --> CD("[6, 7]")
    D --> DA("[7, 2]")
    D --> DB("[7, 3]")
    D --> DC("[7, 6]")
    D --> DD("[7, 7]")

	AA --> AAA("[2, 2, 2]") & AAB("[2, 2, 3]"):::Red & N1("...")
	AB --> ABA("[2, 3, 2]"):::Red & N2("...")

classDef Red fill:#FF4C4C,stroke:#d9d9d9,font-size:14px,text-align:center;

Backtracking the correct way

So, we have to take 1 index and keep on adding it, till we find the solution.

Video explanation

Here is the video explaining this method in detail. Please check it out:

Code

Java

Without using loop

class Solution {

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> ans = new ArrayList<>();
        backtrack(candidates, 0, target, 0, new ArrayList<>(), ans);
        return ans;
    }

    private void backtrack(
        int[] nums,
        int i,
        int target,
        int currSum,
        List<Integer> comb,
        List<List<Integer>> ans
    ) {
        if (currSum == target) {
            ans.add(new ArrayList<>(comb));
            return;
        }
        if (currSum > target || i == nums.length) {
            return;
        }

        // Include nums[i]
        comb.add(nums[i]);
        backtrack(nums, i, target, currSum + nums[i], comb, ans); // Do not move i forward since repetition is allowed
        comb.remove(comb.size() - 1); // Backtrack

        // Exclude nums[i] and move i forward
        backtrack(nums, i + 1, target, currSum, comb, ans);
    }
}

Using the loop

public List<List<Integer>> combinationSum(int[] nums, int target) {  
    List<List<Integer>> ans = new ArrayList<>();  
    Arrays.sort(nums);  
    backtrack(nums, target, 0, new ArrayList<>(), ans);  
    return ans;  
}  
  
private void backtrack(int[] nums, int target, int idx, List<Integer> subAns, List<List<Integer>> ans) {  
    if (target < 0) {  
        return;  
    }  
    if (target == 0) {  
        ans.add(new ArrayList<>(subAns));  
        return;  
    }  
  
    for (int i = idx; i < nums.length; i++) {  
        subAns.add(nums[i]);  
        backtrack(nums, target - nums[i], i, subAns, ans); // not i + 1 because we can reuse same elements  
        subAns.remove(subAns.size() - 1);  
    }  
}

Python

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        ans: List[List[int]] = []

        def backtrack(i: int, currSum: int, comb: List[int]) -> None:
            if currSum == target:
                ans.append(comb[:])  # Add a copy of the current combination
                return
            if currSum > target or i == len(candidates):
                return
            
            # Include candidates[i]
            comb.append(candidates[i])
            backtrack(i, currSum + candidates[i], comb)  # Do not move i forward for repetition
            comb.pop()  # Undo the addition for backtracking
            
            # Exclude candidates[i] and move i forward
            backtrack(i + 1, currSum, comb)

        backtrack(0, 0, [])
        return ans

Complexity

⏰ Time complexity: O(n^d) where n is length of candidates, and d is depth of the tree, which is equal to d = target / min(candidates).
- At each level of the recursion, we explore all possible elements starting from the current candidate's position (due to the ordering constraint). 1. The depth of the recursive tree is determined by how many times we can add the smallest number in candidates before exceeding the target. This is roughly target / min(candidates). Let's call this depth d.
- - At each node, the number of choices (branches) is at most the size of candidates (n). So, in the worst case, the number of nodes explored is proportional to the branching factor raised to the depth: n^d.
🧺 Space complexity: O(d). The recursion depth is at most d = target / min(candidates). Each recursive call takes up space on the call stack.