Combination Sum 2 - Cant Reuse same element
Problem
Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.
Each number in candidates may only be used once in the combination.
Note: The solution set must not contain duplicate combinations.
Examples
Example 1:
Input: candidates = [10,1,2,7,6,1,5], target = 8
Output:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
Example 2:
Input: candidates = [2,5,2,1,2], target = 5
Output:
[
[1,2,2],
[5]
]
Note
- All numbers (including target) will be positive integers.
- Elements in a combination (a1, a2, … , ak) must be in non-descending order. (ie, a1 ≤ a2 ≤ … ≤ ak).
- The solution set must not contain duplicate combinations.
Follow up of [Combination Sum 1](combination-sum-1)
Solution
Method 1 - Backtracking
This problem is an extension of [Combination Sum 1](combination-sum-1).The difference is one number in the array can only be used ONCE.
Lets consider example 1 - [10,1,2,7,6,1,5], target = 8.
This kind of decision tree will result in duplicates, for eg. [1,7] and [7,1] are duplicates:
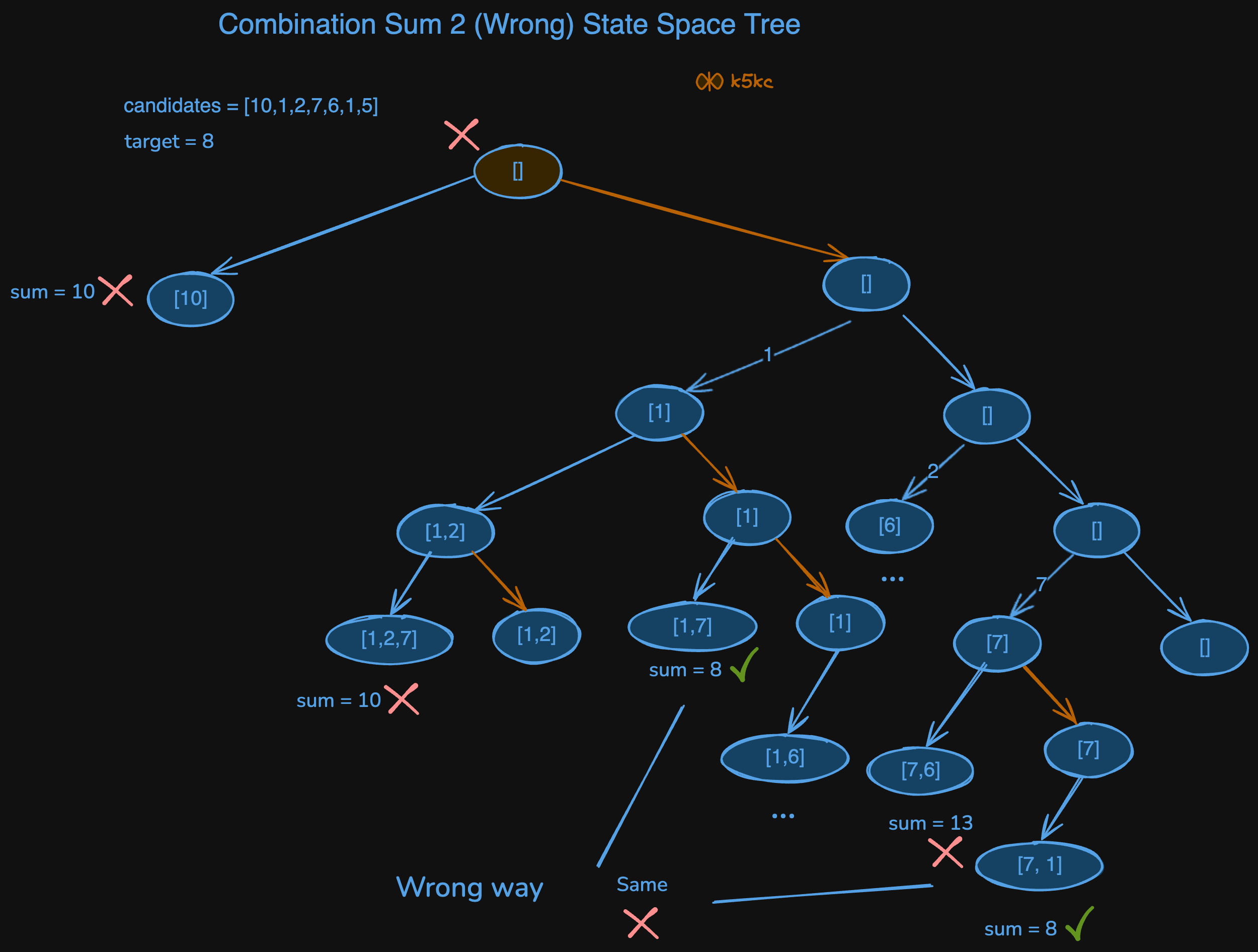
So, we should sort the input array, and then in left choose the number, and in right we dont. Once, we have used the number, we will just keep it in the left subtree.
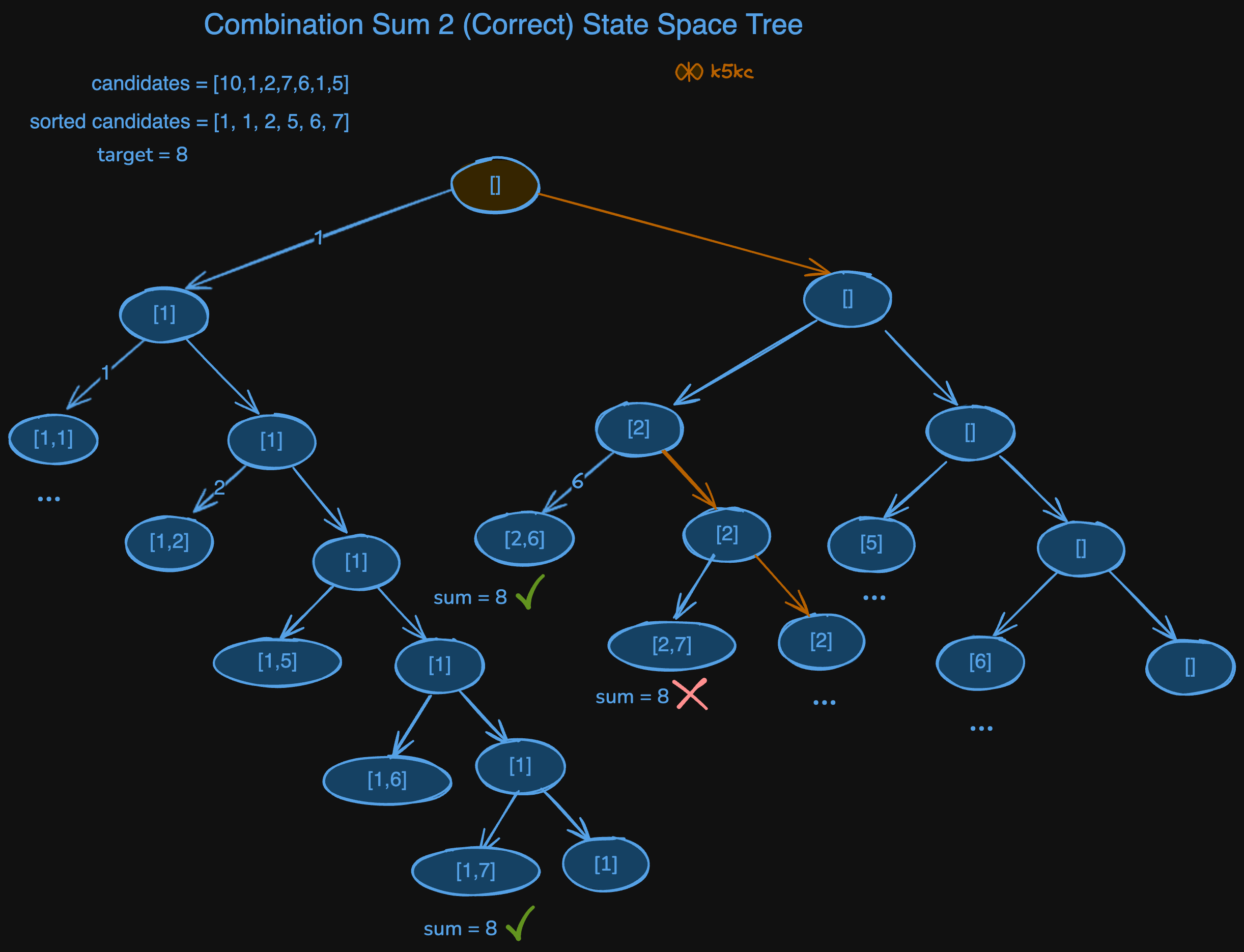
Note, that if we have chosen the candidate, we shouldnt choose it again. So, we are using prev value, to avoid adding duplicates.
Code
Java
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
List<List<Integer>> ans = new ArrayList<> ();
Arrays.sort(candidates);
helper(candidates, target, 0, new ArrayList<Integer>(), ans);
return ans;
}
public void helper(int[] candidates, int target, int idx, List<Integer> subAns, List<List<Integer>> ans) {
if (target == 0) {
ans.add(new ArrayList<Integer> (subAns));
return;
}
if (target<0) {
return;
}
for (int i = idx; i<candidates.length; i++) {
if(i > idx && candidates[i-1] == candidates[i]){
continue;
}
// each time start from different element
subAns.add(candidates[i]);
helper(candidates, target - candidates[i], i+1, subAns, ans); // and use next element only
subAns.remove(subAns.size() - 1);
}
}