Problem

Given an array of distinct integers nums and a target integer target, return the number of possible combinations that add up to target.

The test cases are generated so that the answer can fit in a 32-bit integer.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

Input: nums = [1,2,3], target = 4
Output: 7
Explanation:
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.

Example 2:

1
2

Input: nums = [9], target = 3
Output: 0

Note

This is not Combination sum problem, but Permutation Sum Problem, because [1,1,2] and [2,1,1] are treated differently.

Solution

Method 1 - Recursion

This is the recursion tree:

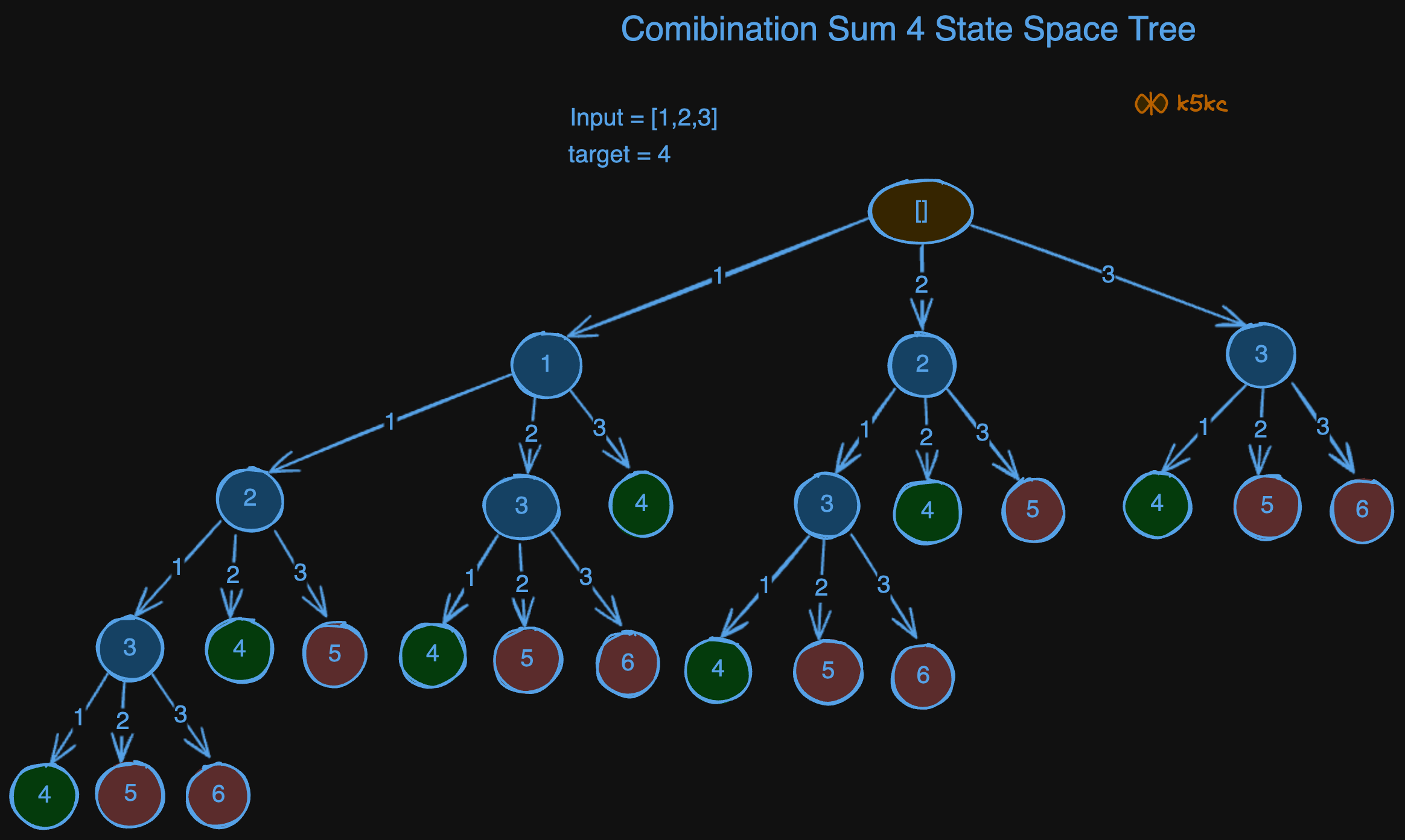
Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

public int combinationSum4(int[] nums, int target) {
    if (target == 0) {
        return 1;
    }
    int count = 0;
    for (int i = 0; i < nums.length; i++) {
        if (nums [i] <= target)
            count += combinationSum4 (nums, target - nums [i]);
    }
    return count;
}

Method 2 - Top Down DP with Memoization

We can see repeating subproblems - for eg. see the node 3, in recursion tree in method 1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

public int combinationSum4(int[] nums, int target) {
	int[] dp = new int[target + 1];
	Arrays.fill(dp, -1);
	dp[0] = 1;
	return backtrack(nums, dp, target);
}
private int backtrack(int[] nums, int[] dp, int sum) {
	if (sum < 0) return 0;
	if (dp[sum] != -1) return dp[sum];
	
	int total = 0;
	
	for (int num : nums) {
		total += backtrack(nums, dp, sum - num);
	}
	
	dp[sum] = total;
	return dp[sum];
}

Method 3 - Bottom up DP

This problem is similar to Coin Change with Fewest Number of Coins Given Infinite Supply. It’s a typical dynamic programming problem.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

public int combinationSum4(int[] nums, int target) {
	if (nums == null || nums.length == 0)
		return 0;

	int[] dp = new int[target + 1];

	dp[0] = 1;

	for (int i = 1; i<= target; i++) {
		for (int num: nums) {
			if (i >= num) {
				dp[i] += dp[i - num];
			}
		}
	}

	return dp[target];
}
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

public int change(int amount, int[] coins) {
	int[] dp = new int[amount + 1];
	dp[0] = 1;
	for (int coin : coins) {
		for (int i = 1; i <= amount; i++) {
			if (i >= coin) {
				dp[i] += dp[i - coin];    
			}
		}
	}
	return dp[amount];
}