Confusing Number

Problem

A confusing number is a number that when rotated 180 degrees becomes a different number with each digit valid.

We can rotate digits of a number by 180 degrees to form new digits.

• When 0, 1, 6, 8, and 9 are rotated 180 degrees, they become 0, 1, 9, 8, and 6 respectively.
• When 2, 3, 4, 5, and 7 are rotated 180 degrees, they become invalid.

Note that after rotating a number, we can ignore leading zeros.

• For example, after rotating 8000, we have 0008 which is considered as just 8.

Given an integer n, return true _if it is aconfusing number , or _false otherwise.

Examples

Example 1:

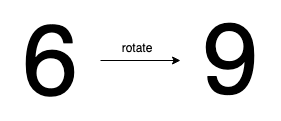
Input: n = 6
Output: true
Explanation: We get 9 after rotating 6, 9 is a valid number, and 9 != 6.

Example 2:

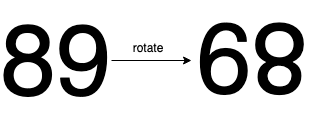
Input: n = 89
Output: true
Explanation: We get 68 after rotating 89, 68 is a valid number and 68 != 89.

Example 3:

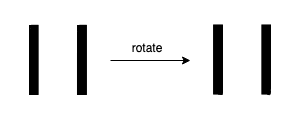
Input: n = 11
Output: false
Explanation: We get 11 after rotating 11, 11 is a valid number but the value remains the same, thus 11 is not a confusing number

Constraints:

• 0 <= n <= 10^9

Solution

Method 1 – Digit Mapping and Reverse Construction

Intuition

A confusing number is one that, when rotated 180 degrees, becomes a different valid number. We can check this by mapping each digit, constructing the rotated number in reverse, and comparing it to the original.

Approach

1. Create a mapping for valid digits: 0→0, 1→1, 6→9, 8→8, 9→6.
2. For each digit in n:
   • If the digit is not valid, return false.
   • Build the rotated number by appending the mapped digit in reverse order.
3. If the rotated number is different from n, return true; else, return false.

Code

C++

class Solution {
public:
    bool confusingNumber(int n) {
        unordered_map<int, int> mp = {{0,0},{1,1},{6,9},{8,8},{9,6}};
        int orig = n, rot = 0;
        while (n > 0) {
            int d = n % 10;
            if (!mp.count(d)) return false;
            rot = rot * 10 + mp[d];
            n /= 10;
        }
        return rot != orig;
    }
};

Go

func ConfusingNumber(n int) bool {
    mp := map[int]int{0:0, 1:1, 6:9, 8:8, 9:6}
    orig, rot := n, 0
    for n > 0 {
        d := n % 10
        v, ok := mp[d]
        if !ok { return false }
        rot = rot*10 + v
        n /= 10
    }
    return rot != orig
}

Java

class Solution {
    public boolean confusingNumber(int n) {
        int orig = n, rot = 0;
        int[] mp = new int[]{0,1,-1,-1,-1,-1,9,-1,8,6};
        while (n > 0) {
            int d = n % 10;
            if (mp[d] == -1) return false;
            rot = rot * 10 + mp[d];
            n /= 10;
        }
        return rot != orig;
    }
}

Kotlin

class Solution {
    fun confusingNumber(n: Int): Boolean {
        val mp = mapOf(0 to 0, 1 to 1, 6 to 9, 8 to 8, 9 to 6)
        var orig = n
        var rot = 0
        var x = n
        while (x > 0) {
            val d = x % 10
            val v = mp[d] ?: return false
            rot = rot * 10 + v
            x /= 10
        }
        return rot != orig
    }
}

Python

class Solution:
    def confusingNumber(self, n: int) -> bool:
        mp = {0:0, 1:1, 6:9, 8:8, 9:6}
        orig, rot = n, 0
        x = n
        while x > 0:
            d = x % 10
            if d not in mp:
                return False
            rot = rot * 10 + mp[d]
            x //= 10
        return rot != orig

Rust

impl Solution {
    pub fn confusing_number(n: i32) -> bool {
        let mp = [(0,0),(1,1),(6,9),(8,8),(9,6)];
        let mut map = std::collections::HashMap::new();
        for (k,v) in mp.iter() { map.insert(*k, *v); }
        let mut orig = n;
        let mut rot = 0;
        let mut x = n;
        while x > 0 {
            let d = x % 10;
            if !map.contains_key(&d) { return false; }
            rot = rot * 10 + map[&d];
            x /= 10;
        }
        rot != orig
    }
}

TypeScript

class Solution {
    confusingNumber(n: number): boolean {
        const mp: Record<number, number> = {0:0, 1:1, 6:9, 8:8, 9:6};
        let orig = n, rot = 0, x = n;
        while (x > 0) {
            const d = x % 10;
            if (!(d in mp)) return false;
            rot = rot * 10 + mp[d];
            x = Math.floor(x / 10);
        }
        return rot !== orig;
    }
}

Complexity

• ⏰ Time complexity: O(log n), where n is the input number. We process each digit once.
• 🧺 Space complexity: O(1), only a few variables are used.