Construct 2D Grid Matching Graph Layout

Problem

You are given a 2D integer array edges representing an undirected graph having n nodes, where edges[i] = [ui, vi] denotes an edge between nodes ui and vi.

Construct a 2D grid that satisfies these conditions:

• The grid contains all nodes from 0 to n - 1 in its cells, with each node appearing exactly once.
• Two nodes should be in adjacent grid cells (horizontally or vertically) if and only if there is an edge between them in edges.

It is guaranteed that edges can form a 2D grid that satisfies the conditions.

Return a 2D integer array satisfying the conditions above. If there are multiple solutions, return any of them.

Examples

Example 1

Input: n = 4, edges = [[0,1],[0,2],[1,3],[2,3]]
Output: [[3,1],[2,0]]

Explanation:

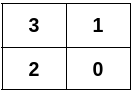
Example 2

Input: n = 5, edges = [[0,1],[1,3],[2,3],[2,4]]
Output: [[4,2,3,1,0]]
Explanation:

Example 3

Input: n = 9, edges =
[[0,1],[0,4],[0,5],[1,7],[2,3],[2,4],[2,5],[3,6],[4,6],[4,7],[6,8],[7,8]]
Output: [[8,6,3],[7,4,2],[1,0,5]]

Explanation:

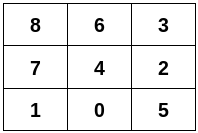
Constraints

• 2 <= n <= 5 * 10^4
• 1 <= edges.length <= 10^5
• edges[i] = [ui, vi]
• 0 <= ui < vi < n
• All the edges are distinct.
• The input is generated such that edges can form a 2D grid that satisfies the conditions.

Solution

Method 1 – BFS Grid Placement

Intuition

Since the graph can be embedded as a grid, we can use BFS to assign each node to a grid cell, starting from any node and placing its neighbors in adjacent cells. We keep track of used grid positions and node-to-position mappings, and reconstruct the grid at the end.

Approach

1. Build the adjacency list from edges.
2. Use BFS to assign each node to a unique grid cell, starting from node 0 at (0,0).
3. For each node, try to place its neighbors in adjacent (up/down/left/right) cells that are not yet used.
4. Track the min/max row and col to determine the grid bounds.
5. After BFS, create a grid of the required size and fill in the node numbers at their positions.
6. Return the grid.

Code

C++

class Solution {
public:
    vector<vector<int>> construct2DGrid(vector<vector<int>>& edges) {
        int n = 0;
        for (auto& e : edges) n = max(n, max(e[0], e[1]));
        n++;
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        map<pair<int,int>, int> pos2node;
        map<int, pair<int,int>> node2pos;
        queue<pair<int,int>> q;
        set<pair<int,int>> used;
        q.push({0,0});
        node2pos[0] = {0,0};
        pos2node[{0,0}] = 0;
        used.insert({0,0});
        vector<int> dr = {0,0,1,-1}, dc = {1,-1,0,0};
        int idx = 1;
        while (!q.empty()) {
            auto [r,c] = q.front(); q.pop();
            int u = pos2node[{r,c}];
            for (int v : g[u]) {
                if (node2pos.count(v)) continue;
                for (int d = 0; d < 4; ++d) {
                    int nr = r + dr[d], nc = c + dc[d];
                    if (!used.count({nr,nc})) {
                        node2pos[v] = {nr,nc};
                        pos2node[{nr,nc}] = v;
                        used.insert({nr,nc});
                        q.push({nr,nc});
                        break;
                    }
                }
            }
        }
        int minr=1e9,maxr=-1e9,minc=1e9,maxc=-1e9;
        for (auto& [node, pos] : node2pos) {
            minr = min(minr, pos.first);
            maxr = max(maxr, pos.first);
            minc = min(minc, pos.second);
            maxc = max(maxc, pos.second);
        }
        int rows = maxr-minr+1, cols = maxc-minc+1;
        vector<vector<int>> grid(rows, vector<int>(cols, -1));
        for (auto& [node, pos] : node2pos) {
            grid[pos.first-minr][pos.second-minc] = node;
        }
        return grid;
    }
};

Go

func Construct2DGrid(edges [][]int) [][]int {
    n := 0
    for _, e := range edges {
        if e[0] > n { n = e[0] }
        if e[1] > n { n = e[1] }
    }
    n++
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    type pos struct{ r, c int }
    pos2node := map[pos]int{}
    node2pos := map[int]pos{}
    used := map[pos]bool{}
    q := []pos{{0, 0}}
    node2pos[0] = pos{0, 0}
    pos2node[pos{0, 0}] = 0
    used[pos{0, 0}] = true
    dr := []int{0, 0, 1, -1}
    dc := []int{1, -1, 0, 0}
    for len(q) > 0 {
        p := q[0]; q = q[1:]
        u := pos2node[p]
        for _, v := range g[u] {
            if _, ok := node2pos[v]; ok { continue }
            for d := 0; d < 4; d++ {
                nr, nc := p.r+dr[d], p.c+dc[d]
                np := pos{nr, nc}
                if !used[np] {
                    node2pos[v] = np
                    pos2node[np] = v
                    used[np] = true
                    q = append(q, np)
                    break
                }
            }
        }
    }
    minr, maxr, minc, maxc := 1<<30, -1<<30, 1<<30, -1<<30
    for _, p := range node2pos {
        if p.r < minr { minr = p.r }
        if p.r > maxr { maxr = p.r }
        if p.c < minc { minc = p.c }
        if p.c > maxc { maxc = p.c }
    }
    rows, cols := maxr-minr+1, maxc-minc+1
    grid := make([][]int, rows)
    for i := range grid { grid[i] = make([]int, cols) }
    for node, p := range node2pos {
        grid[p.r-minr][p.c-minc] = node
    }
    return grid
}

Java

class Solution {
    public int[][] construct2DGrid(int[][] edges) {
        int n = 0;
        for (int[] e : edges) n = Math.max(n, Math.max(e[0], e[1]));
        n++;
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; i++) g.add(new ArrayList<>());
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        Map<String, Integer> pos2node = new HashMap<>();
        Map<Integer, int[]> node2pos = new HashMap<>();
        Queue<int[]> q = new LinkedList<>();
        Set<String> used = new HashSet<>();
        q.offer(new int[]{0,0});
        node2pos.put(0, new int[]{0,0});
        pos2node.put("0,0", 0);
        used.add("0,0");
        int[] dr = {0,0,1,-1}, dc = {1,-1,0,0};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int u = pos2node.get(p[0]+","+p[1]);
            for (int v : g.get(u)) {
                if (node2pos.containsKey(v)) continue;
                for (int d = 0; d < 4; d++) {
                    int nr = p[0]+dr[d], nc = p[1]+dc[d];
                    String key = nr+","+nc;
                    if (!used.contains(key)) {
                        node2pos.put(v, new int[]{nr,nc});
                        pos2node.put(key, v);
                        used.add(key);
                        q.offer(new int[]{nr,nc});
                        break;
                    }
                }
            }
        }
        int minr=Integer.MAX_VALUE,maxr=Integer.MIN_VALUE,minc=Integer.MAX_VALUE,maxc=Integer.MIN_VALUE;
        for (int[] pos : node2pos.values()) {
            minr = Math.min(minr, pos[0]);
            maxr = Math.max(maxr, pos[0]);
            minc = Math.min(minc, pos[1]);
            maxc = Math.max(maxc, pos[1]);
        }
        int rows = maxr-minr+1, cols = maxc-minc+1;
        int[][] grid = new int[rows][cols];
        for (Map.Entry<Integer, int[]> entry : node2pos.entrySet()) {
            int[] pos = entry.getValue();
            grid[pos[0]-minr][pos[1]-minc] = entry.getKey();
        }
        return grid;
    }
}

Kotlin

class Solution {
    fun construct2DGrid(edges: Array<IntArray>): Array<IntArray> {
        var n = 0
        for (e in edges) n = maxOf(n, maxOf(e[0], e[1]))
        n++
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val pos2node = mutableMapOf<Pair<Int,Int>, Int>()
        val node2pos = mutableMapOf<Int, Pair<Int,Int>>()
        val used = mutableSetOf<Pair<Int,Int>>()
        val q = ArrayDeque<Pair<Int,Int>>()
        q.add(0 to 0)
        node2pos[0] = 0 to 0
        pos2node[0 to 0] = 0
        used.add(0 to 0)
        val dr = listOf(0,0,1,-1)
        val dc = listOf(1,-1,0,0)
        while (q.isNotEmpty()) {
            val (r,c) = q.removeFirst()
            val u = pos2node[r to c]!!
            for (v in g[u]) {
                if (node2pos.containsKey(v)) continue
                for (d in 0..3) {
                    val nr = r + dr[d]; val nc = c + dc[d]
                    if ((nr to nc) !in used) {
                        node2pos[v] = nr to nc
                        pos2node[nr to nc] = v
                        used.add(nr to nc)
                        q.add(nr to nc)
                        break
                    }
                }
            }
        }
        var minr=Int.MAX_VALUE; var maxr=Int.MIN_VALUE; var minc=Int.MAX_VALUE; var maxc=Int.MIN_VALUE
        for ((_, pos) in node2pos) {
            minr = minOf(minr, pos.first)
            maxr = maxOf(maxr, pos.first)
            minc = minOf(minc, pos.second)
            maxc = maxOf(maxc, pos.second)
        }
        val rows = maxr-minr+1; val cols = maxc-minc+1
        val grid = Array(rows) { IntArray(cols) }
        for ((node, pos) in node2pos) {
            grid[pos.first-minr][pos.second-minc] = node
        }
        return grid
    }
}

Python

class Solution:
    def construct2DGrid(self, edges: list[list[int]]) -> list[list[int]]:
        from collections import deque, defaultdict
        n = 0
        for u, v in edges:
            n = max(n, u, v)
        n += 1
        g = [[] for _ in range(n)]
        for u, v in edges:
            g[u].append(v)
            g[v].append(u)
        pos2node = {}
        node2pos = {}
        used = set()
        q = deque([(0, 0)])
        node2pos[0] = (0, 0)
        pos2node[(0, 0)] = 0
        used.add((0, 0))
        dr = [0, 0, 1, -1]
        dc = [1, -1, 0, 0]
        while q:
            r, c = q.popleft()
            u = pos2node[(r, c)]
            for v in g[u]:
                if v in node2pos:
                    continue
                for d in range(4):
                    nr, nc = r + dr[d], c + dc[d]
                    if (nr, nc) not in used:
                        node2pos[v] = (nr, nc)
                        pos2node[(nr, nc)] = v
                        used.add((nr, nc))
                        q.append((nr, nc))
                        break
        minr = min(pos[0] for pos in node2pos.values())
        maxr = max(pos[0] for pos in node2pos.values())
        minc = min(pos[1] for pos in node2pos.values())
        maxc = max(pos[1] for pos in node2pos.values())
        rows, cols = maxr - minr + 1, maxc - minc + 1
        grid = [[-1] * cols for _ in range(rows)]
        for node, (r, c) in node2pos.items():
            grid[r - minr][c - minc] = node
        return grid

Rust

impl Solution {
    pub fn construct_2d_grid(edges: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        use std::collections::{VecDeque, HashMap, HashSet};
        let mut n = 0;
        for e in &edges {
            n = n.max(e[0]).max(e[1]);
        }
        n += 1;
        let mut g = vec![vec![]; n as usize];
        for e in &edges {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let mut pos2node = HashMap::new();
        let mut node2pos = HashMap::new();
        let mut used = HashSet::new();
        let mut q = VecDeque::new();
        q.push_back((0, 0));
        node2pos.insert(0, (0, 0));
        pos2node.insert((0, 0), 0);
        used.insert((0, 0));
        let dr = [0, 0, 1, -1];
        let dc = [1, -1, 0, 0];
        while let Some((r, c)) = q.pop_front() {
            let u = *pos2node.get(&(r, c)).unwrap();
            for &v in &g[u] {
                if node2pos.contains_key(&v) { continue; }
                for d in 0..4 {
                    let nr = r + dr[d];
                    let nc = c + dc[d];
                    if !used.contains(&(nr, nc)) {
                        node2pos.insert(v, (nr, nc));
                        pos2node.insert((nr, nc), v);
                        used.insert((nr, nc));
                        q.push_back((nr, nc));
                        break;
                    }
                }
            }
        }
        let minr = node2pos.values().map(|x| x.0).min().unwrap();
        let maxr = node2pos.values().map(|x| x.0).max().unwrap();
        let minc = node2pos.values().map(|x| x.1).min().unwrap();
        let maxc = node2pos.values().map(|x| x.1).max().unwrap();
        let rows = (maxr - minr + 1) as usize;
        let cols = (maxc - minc + 1) as usize;
        let mut grid = vec![vec![-1; cols]; rows];
        for (&node, &(r, c)) in &node2pos {
            grid[(r - minr) as usize][(c - minc) as usize] = node as i32;
        }
        grid
    }
}

TypeScript

class Solution {
    construct2DGrid(edges: number[][]): number[][] {
        let n = 0;
        for (const [u, v] of edges) n = Math.max(n, u, v);
        n++;
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [u, v] of edges) {
            g[u].push(v);
            g[v].push(u);
        }
        const pos2node = new Map<string, number>();
        const node2pos = new Map<number, [number, number]>();
        const used = new Set<string>();
        const q: [number, number][] = [[0, 0]];
        node2pos.set(0, [0, 0]);
        pos2node.set('0,0', 0);
        used.add('0,0');
        const dr = [0, 0, 1, -1], dc = [1, -1, 0, 0];
        while (q.length) {
            const [r, c] = q.shift()!;
            const u = pos2node.get(`${r},${c}`)!;
            for (const v of g[u]) {
                if (node2pos.has(v)) continue;
                for (let d = 0; d < 4; d++) {
                    const nr = r + dr[d], nc = c + dc[d];
                    const key = `${nr},${nc}`;
                    if (!used.has(key)) {
                        node2pos.set(v, [nr, nc]);
                        pos2node.set(key, v);
                        used.add(key);
                        q.push([nr, nc]);
                        break;
                    }
                }
            }
        }
        let minr = Infinity, maxr = -Infinity, minc = Infinity, maxc = -Infinity;
        for (const [_, [r, c]] of node2pos) {
            minr = Math.min(minr, r);
            maxr = Math.max(maxr, r);
            minc = Math.min(minc, c);
            maxc = Math.max(maxc, c);
        }
        const rows = maxr - minr + 1, cols = maxc - minc + 1;
        const grid: number[][] = Array.from({length: rows}, () => Array(cols).fill(-1));
        for (const [node, [r, c]] of node2pos) {
            grid[r - minr][c - minc] = node;
        }
        return grid;
    }
}

Complexity

• ⏰ Time complexity: O(n), where n is the number of nodes. Each node and edge is processed once.
• 🧺 Space complexity: O(n), for the grid and mappings.