Problem

A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.

The world is modeled as an m x n binary grid isInfected, where isInfected[i][j] == 0 represents uninfected cells, and isInfected[i][j] == 1 represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two 4-directionally adjacent cells, on the shared boundary.

Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region (i.e., the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night).

There will never be a tie.

Return the number of walls used to quarantine all the infected regions. If the world will become fully infected, return the number of walls used.

Examples

Example 1

1
2

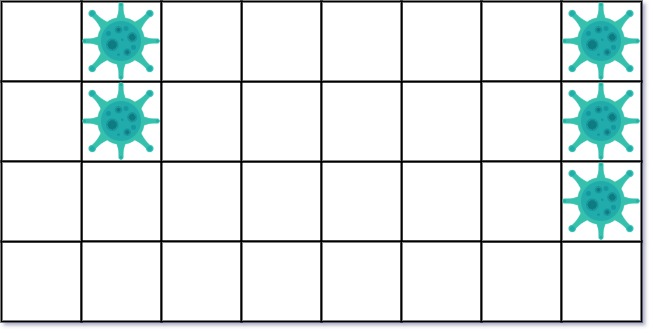
Input: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
Output: 10

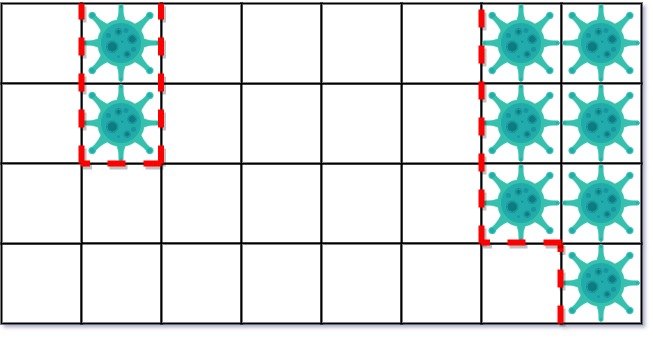
Explanation: There are 2 contaminated regions. On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is: 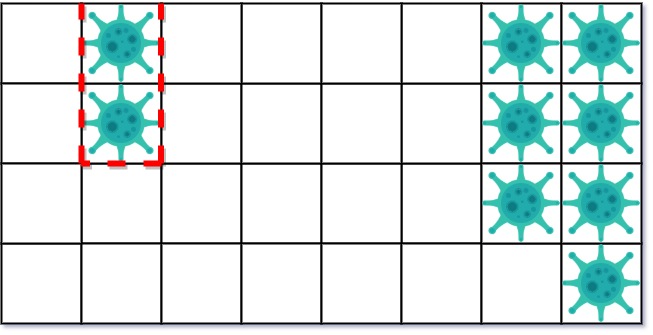On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained.

Example 2

1
2
3
4

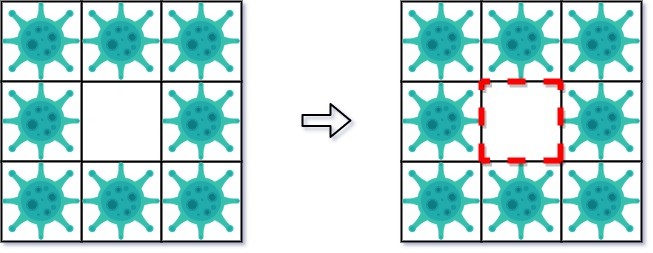
Input: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
Output: 4
Explanation: Even though there is only one cell saved, there are 4 walls built.
Notice that walls are only built on the shared boundary of two different cells.

Example 3

1
2
3

Input: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
Output: 13
Explanation: The region on the left only builds two new walls.

Constraints

  • m == isInfected.length
  • n == isInfected[i].length
  • 1 <= m, n <= 50
  • isInfected[i][j] is either 0 or 1.
  • There is always a contiguous viral region throughout the described process that will infect strictly more uncontaminated squares in the next round.

Solution

Method 1 - Simulation

Intuition

We simulate each turn of the process and repeat as long as infected regions remain.

Algorithm

Although the implementation is lengthy, the steps are clear: Identify all infected regions (connected components), recording for each the frontier (adjacent uninfected cells) and its perimeter. Quarantine the region that threatens the most uninfected cells, adding its perimeter to the total. Allow the virus to spread outward by one cell in all other regions.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

import java.util.*;
class Solution {
    private int m, n;
    private int[] dr = {-1, 1, 0, 0};
    private int[] dc = {0, 0, -1, 1};

    public int containVirus(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        int ans = 0;
        while (true) {
            Set<Integer> seen = new HashSet<>();
            List<Set<Integer>> regions = new ArrayList<>();
            List<Set<Integer>> frontiers = new ArrayList<>();
            List<Integer> perimeters = new ArrayList<>();
            for (int r = 0; r < m; r++) {
                for (int c = 0; c < n; c++) {
                    if (grid[r][c] == 1 && !seen.contains(r * n + c)) {
                        regions.add(new HashSet<>());
                        frontiers.add(new HashSet<>());
                        perimeters.add(0);
                        dfs(r, c, grid, seen, regions, frontiers, perimeters);
                    }
                }
            }
            if (regions.isEmpty()) break;
            int triage = 0;
            for (int i = 1; i < frontiers.size(); i++) {
                if (frontiers.get(i).size() > frontiers.get(triage).size()) triage = i;
            }
            ans += perimeters.get(triage);
            for (int i = 0; i < regions.size(); i++) {
                if (i == triage) {
                    for (int code : regions.get(i)) {
                        grid[code / n][code % n] = -1;
                    }
                } else {
                    for (int code : regions.get(i)) {
                        int r = code / n, c = code % n;
                        for (int k = 0; k < 4; k++) {
                            int nr = r + dr[k], nc = c + dc[k];
                            if (0 <= nr && nr < m && 0 <= nc && nc < n && grid[nr][nc] == 0) {
                                grid[nr][nc] = 1;
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }

    private void dfs(int r, int c, int[][] grid, Set<Integer> seen, List<Set<Integer>> regions, List<Set<Integer>> frontiers, List<Integer> perimeters) {
        int code = r * n + c;
        if (!seen.contains(code)) {
            seen.add(code);
            int N = regions.size();
            regions.get(N - 1).add(code);
            for (int k = 0; k < 4; k++) {
                int nr = r + dr[k], nc = c + dc[k];
                if (0 <= nr && nr < m && 0 <= nc && nc < n) {
                    if (grid[nr][nc] == 1) {
                        dfs(nr, nc, grid, seen, regions, frontiers, perimeters);
                    } else if (grid[nr][nc] == 0) {
                        frontiers.get(N - 1).add(nr * n + nc);
                        perimeters.set(N - 1, perimeters.get(N - 1) + 1);
                    }
                }
            }
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution:
    def containVirus(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dr, dc = [-1, 1, 0, 0], [0, 0, -1, 1]
        ans = 0
        while True:
            seen = set()
            regions, frontiers, perimeters = [], [], []
            for r in range(m):
                for c in range(n):
                    if grid[r][c] == 1 and (r * n + c) not in seen:
                        regions.append(set())
                        frontiers.append(set())
                        perimeters.append(0)
                        self.dfs(r, c, grid, seen, regions, frontiers, perimeters, dr, dc, m, n)
            if not regions:
                break
            triage = max(range(len(frontiers)), key=lambda i: len(frontiers[i]))
            ans += perimeters[triage]
            for i in range(len(regions)):
                if i == triage:
                    for code in regions[i]:
                        grid[code // n][code % n] = -1
                else:
                    for code in regions[i]:
                        r, c = code // n, code % n
                        for k in range(4):
                            nr, nc = r + dr[k], c + dc[k]
                            if 0 <= nr < m and 0 <= nc < n and grid[nr][nc] == 0:
                                grid[nr][nc] = 1
        return ans

    def dfs(self, r: int, c: int, grid, seen, regions, frontiers, perimeters, dr, dc, m, n):
        if (r * n + c) not in seen:
            seen.add(r * n + c)
            N = len(regions)
            regions[N-1].add(r * n + c)
            for k in range(4):
                nr, nc = r + dr[k], c + dc[k]
                if 0 <= nr < m and 0 <= nc < n:
                    if grid[nr][nc] == 1:
                        self.dfs(nr, nc, grid, seen, regions, frontiers, perimeters, dr, dc, m, n)
                    elif grid[nr][nc] == 0:
                        frontiers[N-1].add(nr * n + nc)
                        perimeters[N-1] += 1

Complexity

⏰ Time complexity: O((mn)^2), where m and n are the grid dimensions. Each turn may visit all cells, and there can be up to mn turns in the worst case. 🧺 Space complexity: O(mn), for the sets and recursion stack.