Convert BST to Greater Sum Tree

Problem

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

Examples

Example 1:

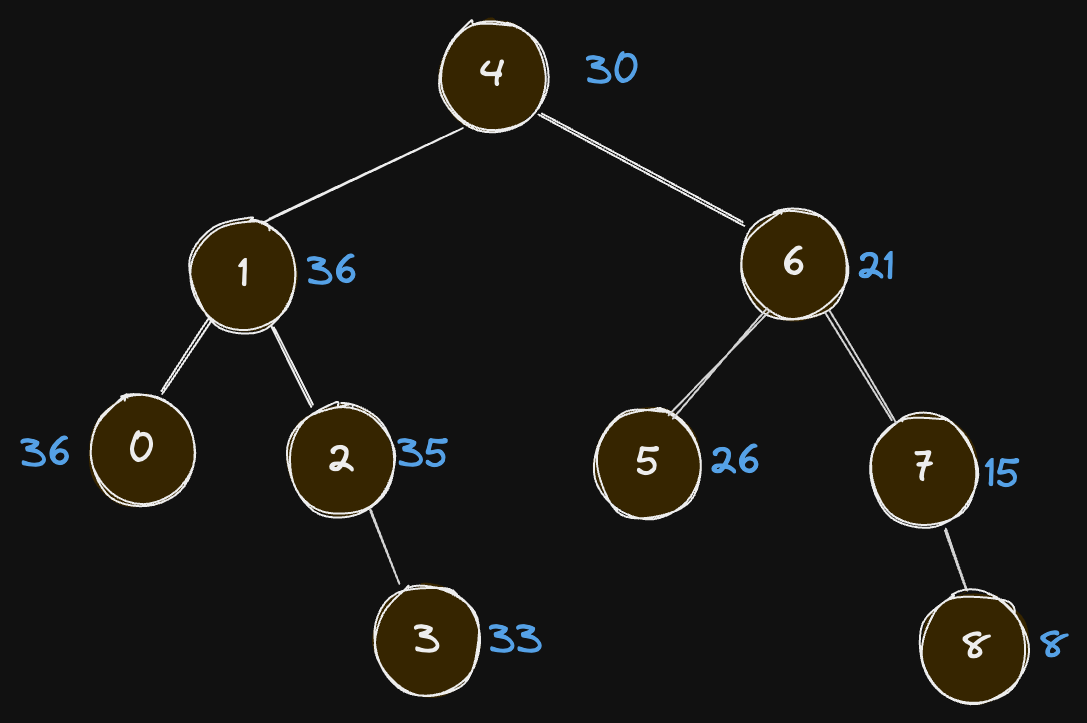
Input:
root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output:
 [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input:
root = [0,null,1]
Output:
 [1,null,1]

Solution

Method 1 - Brute Force

Naive approach will be for every node, traverse the tree and find out all the nodes which are greater and update the node. But the time complexity of this approach will be O(n^2).

Method 2 - Recursive Reverse Inorder Traversal

Since this is a BST, the right most node in the BST is the biggest node among all the nodes. So, we can start from right, i.e. we do a reverse inorder traversal to traverse the nodes of the tree in descending order. Since we are visiting the nodes in the decreasing order, all we care about is maintaining the running sum of the nodes visited thus far.

In the process, we keep track of the running sum of all nodes which we have traversed thus far.

Video Explanation

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/b37dAlprb6k" frameborder="0" allowfullscreen></iframe></div>

Code

Java

Using global variables

public class Solution {
	private int sum = 0;
	public TreeNode bstToGst(TreeNode root) {
		if (root == null) {
			return null;
		}
		
		bstToGst(root.right); //visit the right node first

		sum += root.val; //update the sum for the next node
		root.val = sum;
		
		bstToGst(root.left);	
		return root;	
	}
}

Without using global variables with object

class Solution {

	public TreeNode bstToGst(TreeNode root) {
		reverseInorder(root, new TreeNode(0));
		return root;
	}

	private void reverseInorder(TreeNode root, TreeNode sum) {
		if (root == null) {
			return;
		}

		int right = reverseInorder(root.right, sum);
		sum.val += root.val;
		root.val = sum.val;
		return reverseInorder(root.left, sum);
	}
}

Without using global variables with primitive

We can also just passed the primitive sum, but return int in reverseInorder() method.

class Solution {

	public TreeNode bstToGst(TreeNode root) {
		reverseInorder(root, 0);
		return root;
	}

	private int reverseInorder(TreeNode root, int sum) {
		if (root == null) {
			return sum;
		}

		int right = reverseInorder(root.right, sum); // pass in provided sum for accumulation
		root.val = root.val + right;
		return reverseInorder(root.left, root.val); // pass in updated sum
	}
}

Python

Using Global variables

# Using global variable
class Solution:
	def __init__(self):
		self.sum = 0

	def bstToGst(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
		if root is None:
			return None
		self.bstToGst(root.right)
		self.sum += root.val
		root.val = self.sum
		self.bstToGst(root.left)
		return root

Without using global variables with object

# Without global variable, using object
class Solution:
	def bstToGst(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
		class Sum:
			def __init__(self):
				self.val = 0
		def reverseInorder(node: Optional[TreeNode], sum_obj: Sum) -> None:
			if node is None:
				return
			reverseInorder(node.right, sum_obj)
			sum_obj.val += node.val
			node.val = sum_obj.val
			reverseInorder(node.left, sum_obj)
		reverseInorder(root, Sum())
		return root

Without global variable, using primitive

class SolutionPrimitive:
	def bstToGst(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
		def reverseInorder(node: Optional[TreeNode], acc: int) -> int:
			if node is None:
				return acc
			right_sum = reverseInorder(node.right, acc)
			node.val += right_sum
			return reverseInorder(node.left, node.val)
		reverseInorder(root, 0)
		return root

Complexity

• ⏰ Time complexity: O(n), where n is number of nodes in tree.
• 🧺 Space complexity: O(n) for using recursive stack

Method 3 - Iterative Reverse Inorder Traversal

Initially, use curr to point to the root,

1. push into Stack the right-most path of current subtree;
2. pop out a node, update sum and the node value;
3. point curr to the node's left child, if any; Repeat the above till the stack is empty and curr has no left child.

Code

Java

class Solution {
    public TreeNode bstToGst(TreeNode root) {
        Deque<TreeNode> stk = new ArrayDeque<>();
        TreeNode curr = root;
        int sum = 0;
        while (curr != null || !stk.isEmpty()) {
            while (curr != null) { // save right-most path of the current subtree
                stk.push(curr);
                curr = curr.right;
            }
            curr = stk.pop(); // pop out by reversed in-order.
            sum += curr.val; // update sum.
            curr.val = sum; // update node value.
            curr = curr.left; // move to left branch.
        }    
        return root;
    }
}

Python

class Solution:
	def bstToGst(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
		stack: list[TreeNode] = []
		curr = root
		total = 0
		while curr is not None or stack:
			while curr is not None:
				stack.append(curr)
				curr = curr.right
			curr = stack.pop()
			total += curr.val
			curr.val = total
			curr = curr.left
		return root

Complexity

• ⏰ Time complexity: O(n), where n is number of nodes in tree.
• 🧺 Space complexity: O(n) for using stack