Convert Sorted Array to height-balanced Binary Search Tree

Problem

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

Examples

Example 1:

Input: nums = [1, 2, 3, 4, 5, 6]
Output: [3,2,5,1,null,4,6]
Explanation: [4,2,5,1,3,null,6] is also accepted.

These are the two height-balanced binary tree, with height = 3:

    3
   / \
  2   5
 /   / \
1   4   6

OR

    4
   / \
  2   5
 / \   \
1   3   6

Note, that we may also get skewed binary search tree, but we don't want that, height = 6 is not minimum

1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

Solution

Why minimal height is important?

We can perform a linear scan of the array, using the first element as the root and inserting subsequent elements into the tree. However, this would result in a skewed tree, with all nodes on one side, causing the tree height to equal the number of elements. Our goal is to keep the tree as balanced as possible.

Definition: Balanced Binary Search Tree BBST Data Structures

Method 1 - Recursive Preorder Traversal

Here are the steps:

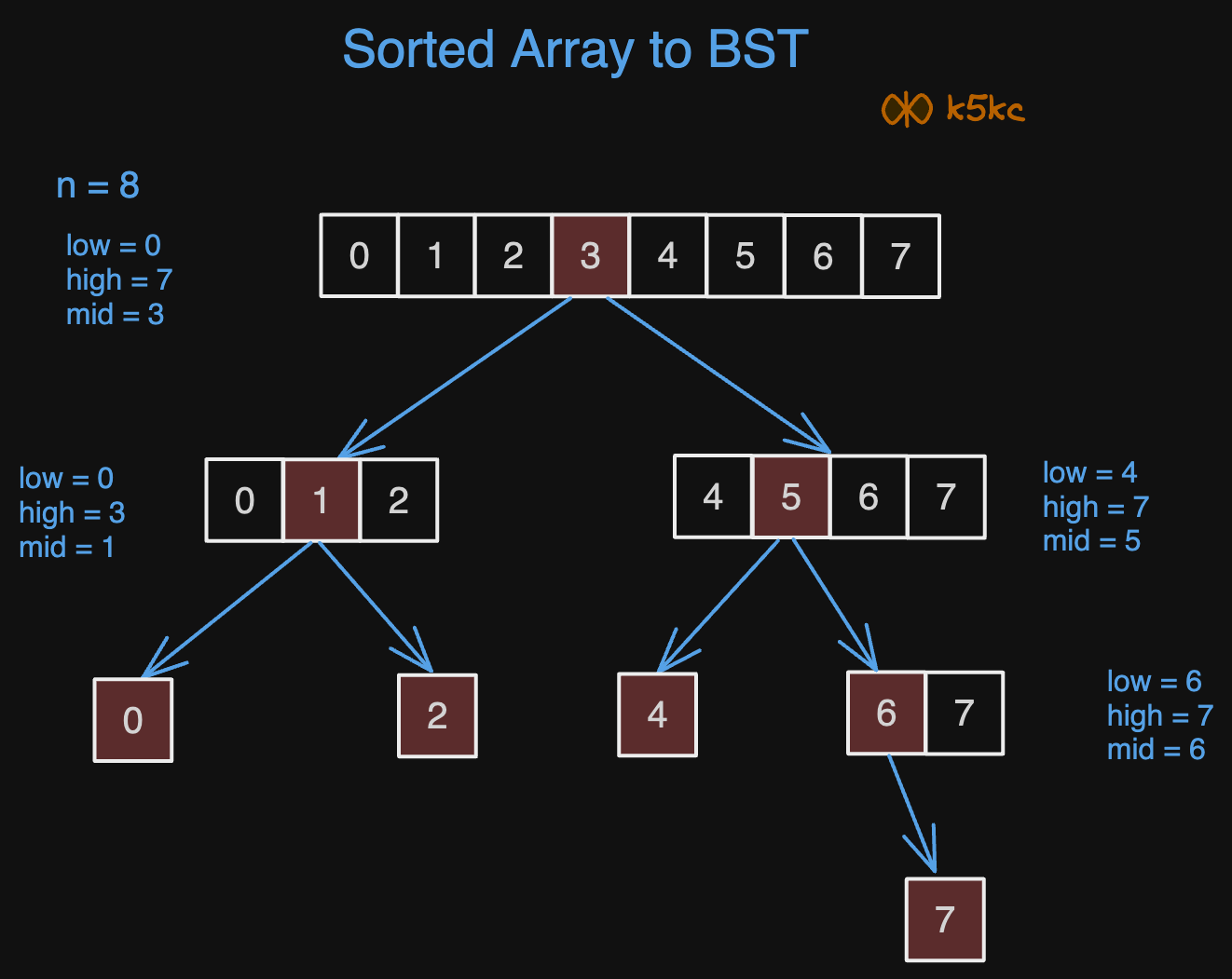
1. Find the middle element of the array.
2. Make it root to ensure half of the array elements are on the left and half on the right.
3. Recursively process the left half of the array and set it as root.left.
4. Recursively process the right half of the array and set it as root.right.
5. Return the root.

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/zBUFWGfz07E" frameborder="0" allowfullscreen></iframe></div>

Code

Java

class Solution {

	public TreeNode sortedArrayToBST(int[] nums) {
		if (nums.length == 0) {
			return null;
		}

		TreeNode head = helper(nums, 0, nums.length - 1);
		return head;
	}

	public TreeNode helper(int[] nums, int low, int high) {
		if (low > high) { // Done
			return null;
		}

		int mid = (low + high) / 2;
		TreeNode node = new TreeNode(nums[mid]);
		node.left = helper(nums, low, mid - 1);
		node.right = helper(nums, mid + 1, high);
		return node;
	}

}

Python

class Solution:
  def sortedArrayToBST(self, nums: list[int]) -> 'TreeNode | None':
    if not nums:
      return None

    def helper(low: int, high: int) -> 'TreeNode | None':
      if low > high:
        return None
      mid = (low + high) // 2
      node = TreeNode(nums[mid])
      node.left = helper(low, mid - 1)
      node.right = helper(mid + 1, high)
      return node

    return helper(0, len(nums) - 1)

Complexity

• ⏰ Time complexity: O(n) where n is the length of array
• 🧺 Space complexity: O(log n) as log n is the height of the tree.