Count Artifacts That Can Be Extracted

Problem

There is an n x n 0-indexed grid with some artifacts buried in it. You are given the integer n and a 0-indexed 2D integer array artifacts describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where:

(r1i, c1i) is the coordinate of the top-left cell of the ith artifact and
(r2i, c2i) is the coordinate of the bottom-right cell of the ith artifact.

You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.

Given a 0-indexed 2D integer array dig where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return the number of artifacts that you can extract.

The test cases are generated such that:

No two artifacts overlap.
Each artifact only covers at most 4 cells.
The entries of dig are unique.

Examples

Example 1


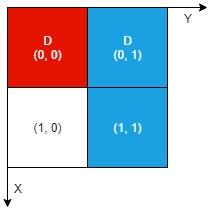
![](https://assets.leetcode.com/uploads/2019/09/16/untitled-diagram.jpg)

Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
Output: 1
Explanation: 
The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid.
There is 1 artifact that can be extracted, namely the red artifact.
The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it.
Thus, we return 1.

Example 2


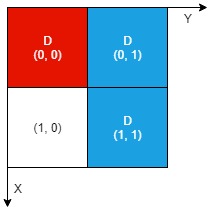
![](https://assets.leetcode.com/uploads/2019/09/16/untitled-diagram-1.jpg)

Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
Output: 2
Explanation: Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.

Constraints

1 <= n <= 1000
1 <= artifacts.length, dig.length <= min(n2, 105)
artifacts[i].length == 4
dig[i].length == 2
0 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1
r1i <= r2i
c1i <= c2i
No two artifacts will overlap.
The number of cells covered by an artifact is at most 4.
The entries of dig are unique.

Solution

Method 1 – Set Coverage Simulation 1

Intuition

Each artifact covers a set of cells. If all the cells of an artifact are dug, the artifact can be extracted. We can use a set to record all dug cells and check for each artifact if all its cells are in the set.

Approach

Store all dug cells in a set for O(1) lookup.
For each artifact, enumerate all its covered cells.
Check if all cells of the artifact are in the dug set.
Count the number of artifacts that can be fully extracted.

Code

C++

class Solution {
public:
    int digArtifacts(int n, vector<vector<int>>& artifacts, vector<vector<int>>& dig) {
        set<pair<int, int>> dug;
        for (auto& d : dig) dug.insert({d[0], d[1]});
        int ans = 0;
        for (auto& a : artifacts) {
            bool ok = true;
            for (int i = a[0]; i <= a[2]; ++i) {
                for (int j = a[1]; j <= a[3]; ++j) {
                    if (!dug.count({i, j})) ok = false;
                }
            }
            if (ok) ++ans;
        }
        return ans;
    }
};

Go

func digArtifacts(n int, artifacts [][]int, dig [][]int) int {
    dug := map[[2]int]bool{}
    for _, d := range dig {
        dug[[2]int{d[0], d[1]}] = true
    }
    ans := 0
    for _, a := range artifacts {
        ok := true
        for i := a[0]; i <= a[2]; i++ {
            for j := a[1]; j <= a[3]; j++ {
                if !dug[[2]int{i, j}] {
                    ok = false
                }
            }
        }
        if ok {
            ans++
        }
    }
    return ans
}

Java

class Solution {
    public int digArtifacts(int n, int[][] artifacts, int[][] dig) {
        Set<String> dug = new HashSet<>();
        for (int[] d : dig) dug.add(d[0] + "," + d[1]);
        int ans = 0;
        for (int[] a : artifacts) {
            boolean ok = true;
            for (int i = a[0]; i <= a[2]; ++i) {
                for (int j = a[1]; j <= a[3]; ++j) {
                    if (!dug.contains(i + "," + j)) ok = false;
                }
            }
            if (ok) ans++;
        }
        return ans;
    }
}

Kotlin

class Solution {
    fun digArtifacts(n: Int, artifacts: Array<IntArray>, dig: Array<IntArray>): Int {
        val dug = mutableSetOf<Pair<Int, Int>>() 
        for (d in dig) dug.add(Pair(d[0], d[1]))
        var ans = 0
        for (a in artifacts) {
            var ok = true
            for (i in a[0]..a[2]) {
                for (j in a[1]..a[3]) {
                    if (Pair(i, j) !in dug) ok = false
                }
            }
            if (ok) ans++
        }
        return ans
    }
}

Python

class Solution:
    def digArtifacts(self, n: int, artifacts: list[list[int]], dig: list[list[int]]) -> int:
        dug = set((r, c) for r, c in dig)
        ans = 0
        for r1, c1, r2, c2 in artifacts:
            if all((i, j) in dug for i in range(r1, r2+1) for j in range(c1, c2+1)):
                ans += 1
        return ans

Rust

impl Solution {
    pub fn dig_artifacts(_n: i32, artifacts: Vec<Vec<i32>>, dig: Vec<Vec<i32>>) -> i32 {
        use std::collections::HashSet;
        let dug: HashSet<(i32, i32)> = dig.iter().map(|d| (d[0], d[1])).collect();
        let mut ans = 0;
        for a in artifacts {
            let mut ok = true;
            for i in a[0]..=a[2] {
                for j in a[1]..=a[3] {
                    if !dug.contains(&(i, j)) {
                        ok = false;
                    }
                }
            }
            if ok {
                ans += 1;
            }
        }
        ans
    }
}

TypeScript

class Solution {
    digArtifacts(n: number, artifacts: number[][], dig: number[][]): number {
        const dug = new Set(dig.map(([r, c]) => r + ',' + c));
        let ans = 0;
        for (const [r1, c1, r2, c2] of artifacts) {
            let ok = true;
            for (let i = r1; i <= r2; ++i) {
                for (let j = c1; j <= c2; ++j) {
                    if (!dug.has(i + ',' + j)) ok = false;
                }
            }
            if (ok) ans++;
        }
        return ans;
    }
}

Complexity

⏰ Time complexity: O(A * S), where A is the number of artifacts and S is the maximum number of cells per artifact (at most 4), plus O(D) for the number of dig cells.
🧺 Space complexity: O(D), for the set of dug cells.