Count Connected Components in LCM Graph
Problem
You are given an array of integers nums of size n and a positive integer threshold.
There is a graph consisting of n nodes with the ith node having a value of
nums[i]. Two nodes i and j in the graph are connected via an
undirected edge if lcm(nums[i], nums[j]) <= threshold.
Return the number of connected components in this graph.
A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.
The term lcm(a, b) denotes the least common multiple of a and b.
Examples
Example 1
Input: nums = [2,4,8,3,9], threshold = 5
Output: 4
Explanation:
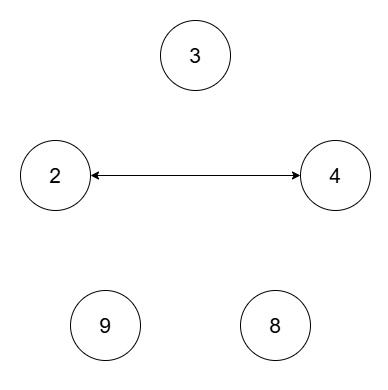
The four connected components are `(2, 4)`, `(3)`, `(8)`, `(9)`.
Example 2
Input: nums = [2,4,8,3,9,12], threshold = 10
Output: 2
Explanation:
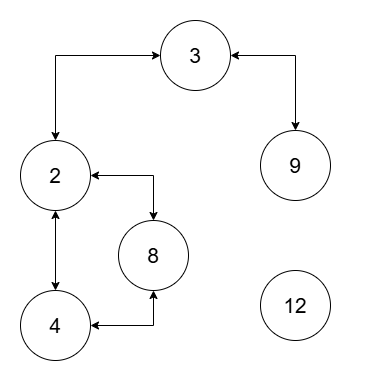
The two connected components are `(2, 3, 4, 8, 9)`, and `(12)`.
Constraints
1 <= nums.length <= 10^51 <= nums[i] <= 10^9- All elements of
numsare unique. 1 <= threshold <= 2 * 10^5
Solution
Method 1 – Union-Find with Divisor Grouping
Intuition
If lcm(a, b) ≤ threshold, then both a and b must be divisible by some integer d > threshold / max(a, b). Instead of checking all pairs, we can group numbers by their divisors greater than threshold and union them. Each group forms a connected component.
Approach
- For each number from threshold + 1 up to the max value in nums:
- For each multiple of this number, if it exists in nums, union it with the base number.
- Use a union-find (disjoint set) structure to group connected numbers.
- The number of unique parents in the union-find structure is the answer.
Code
C++
class Solution {
public:
int countComponents(vector<int>& nums, int threshold) {
int n = nums.size();
unordered_map<int, int> idx;
for (int i = 0; i < n; ++i) idx[nums[i]] = i;
vector<int> par(n);
iota(par.begin(), par.end(), 0);
function<int(int)> find = [&](int x) { return par[x] == x ? x : par[x] = find(par[x]); };
int mx = *max_element(nums.begin(), nums.end());
for (int d = threshold + 1; d <= mx; ++d) {
int root = -1;
for (int m = d; m <= mx; m += d) {
if (idx.count(m)) {
if (root == -1) root = idx[m];
else par[find(idx[m])] = find(root);
}
}
}
unordered_set<int> comps;
for (int i = 0; i < n; ++i) comps.insert(find(i));
return comps.size();
}
};
Go
func countComponents(nums []int, threshold int) int {
n := len(nums)
idx := map[int]int{}
for i, v := range nums { idx[v] = i }
par := make([]int, n)
for i := range par { par[i] = i }
var find func(int) int
find = func(x int) int {
if par[x] != x { par[x] = find(par[x]) }
return par[x]
}
mx := 0
for _, v := range nums { if v > mx { mx = v } }
for d := threshold + 1; d <= mx; d++ {
root := -1
for m := d; m <= mx; m += d {
if i, ok := idx[m]; ok {
if root == -1 { root = i } else { par[find(i)] = find(root) }
}
}
}
comps := map[int]bool{}
for i := 0; i < n; i++ { comps[find(i)] = true }
return len(comps)
}
Java
class Solution {
public int countComponents(int[] nums, int threshold) {
int n = nums.length;
Map<Integer, Integer> idx = new HashMap<>();
for (int i = 0; i < n; i++) idx.put(nums[i], i);
int[] par = new int[n];
for (int i = 0; i < n; i++) par[i] = i;
int mx = Arrays.stream(nums).max().getAsInt();
for (int d = threshold + 1; d <= mx; d++) {
int root = -1;
for (int m = d; m <= mx; m += d) {
if (idx.containsKey(m)) {
if (root == -1) root = idx.get(m);
else par[find(par, idx.get(m))] = find(par, root);
}
}
}
Set<Integer> comps = new HashSet<>();
for (int i = 0; i < n; i++) comps.add(find(par, i));
return comps.size();
}
private int find(int[] par, int x) {
if (par[x] != x) par[x] = find(par, par[x]);
return par[x];
}
}
Kotlin
class Solution {
fun countComponents(nums: IntArray, threshold: Int): Int {
val n = nums.size
val idx = nums.withIndex().associate { it.value to it.index }
val par = IntArray(n) { it }
fun find(x: Int): Int {
if (par[x] != x) par[x] = find(par[x])
return par[x]
}
val mx = nums.maxOrNull()!!
for (d in threshold + 1..mx) {
var root = -1
var m = d
while (m <= mx) {
idx[m]?.let {
if (root == -1) root = it
else par[find(it)] = find(root)
}
m += d
}
}
return (0 until n).map { find(it) }.toSet().size
}
}
Python
class Solution:
def countComponents(self, nums: list[int], threshold: int) -> int:
n = len(nums)
idx = {v: i for i, v in enumerate(nums)}
par = list(range(n))
def find(x):
if par[x] != x:
par[x] = find(par[x])
return par[x]
mx = max(nums)
for d in range(threshold + 1, mx + 1):
root = -1
for m in range(d, mx + 1, d):
if m in idx:
if root == -1:
root = idx[m]
else:
par[find(idx[m])] = find(root)
return len({find(i) for i in range(n)})
Rust
use std::collections::{HashMap, HashSet};
impl Solution {
pub fn count_components(nums: Vec<i32>, threshold: i32) -> i32 {
let n = nums.len();
let mut idx = HashMap::new();
for (i, &v) in nums.iter().enumerate() { idx.insert(v, i); }
let mut par: Vec<usize> = (0..n).collect();
fn find(par: &mut Vec<usize>, x: usize) -> usize {
if par[x] != x { par[x] = find(par, par[x]); }
par[x]
}
let mx = *nums.iter().max().unwrap();
for d in (threshold + 1)..=mx {
let mut root = None;
let mut m = d;
while m <= mx {
if let Some(&i) = idx.get(&m) {
if root.is_none() { root = Some(i); }
else {
let r = root.unwrap();
let fi = find(&mut par, i);
let fr = find(&mut par, r);
par[fi] = fr;
}
}
m += d;
}
}
let mut comps = HashSet::new();
for i in 0..n { comps.insert(find(&mut par, i)); }
comps.len() as i32
}
}
TypeScript
class Solution {
countComponents(nums: number[], threshold: number): number {
const n = nums.length;
const idx: Record<number, number> = {};
for (let i = 0; i < n; i++) idx[nums[i]] = i;
const par = Array.from({length: n}, (_, i) => i);
const find = (x: number): number => par[x] === x ? x : (par[x] = find(par[x]));
const mx = Math.max(...nums);
for (let d = threshold + 1; d <= mx; d++) {
let root = -1;
for (let m = d; m <= mx; m += d) {
if (idx[m] !== undefined) {
if (root === -1) root = idx[m];
else par[find(idx[m])] = find(root);
}
}
}
const comps = new Set<number>();
for (let i = 0; i < n; i++) comps.add(find(i));
return comps.size;
}
}
Complexity
- ⏰ Time complexity:
O(n + T log n), where T is the threshold and n is the number of elements, due to union-find and divisor grouping. - 🧺 Space complexity:
O(n + T), for the parent array and index mapping.