problemhardalgorithmsleetcode-2088leetcode 2088leetcode2088

Count Fertile Pyramids in a Land

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

A farmer has a rectangular grid of land with m rows and n columns that can be divided into unit cells. Each cell is either fertile (represented by a 1) or barren (represented by a 0). All cells outside the grid are considered barren.

A pyramidal plot of land can be defined as a set of cells with the following criteria:

  1. The number of cells in the set has to be greater than1 and all cells must be fertile.
  2. The apex of a pyramid is the topmost cell of the pyramid. The height of a pyramid is the number of rows it covers. Let (r, c) be the apex of the pyramid, and its height be h. Then, the plot comprises of cells (i, j) where r <= i <= r + h - 1 and c - (i - r) <= j <= c + (i - r).

An inverse pyramidal plot of land can be defined as a set of cells with similar criteria:

  1. The number of cells in the set has to be greater than1 and all cells must be fertile.
  2. The apex of an inverse pyramid is the bottommost cell of the inverse pyramid. The height of an inverse pyramid is the number of rows it covers. Let (r, c) be the apex of the pyramid, and its height be h. Then, the plot comprises of cells (i, j) where r - h + 1 <= i <= r and c - (r - i) <= j <= c + (r - i).

Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.

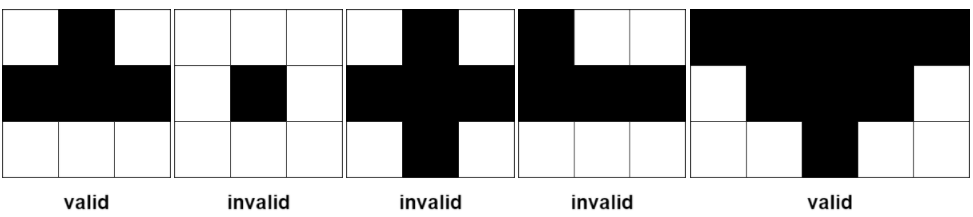
Given a 0-indexed m x n binary matrix grid representing the farmland, return thetotal number of pyramidal and inverse pyramidal plots that can be found in grid.

Examples

Example 1


![](https://assets.leetcode.com/uploads/2021/12/22/1.JPG)

    
    
    Input: grid = [[0,1,1,0],[1,1,1,1]]
    Output: 2
    Explanation: The 2 possible pyramidal plots are shown in blue and red respectively.
    There are no inverse pyramidal plots in this grid. 
    Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.

Example 2


![](https://assets.leetcode.com/uploads/2021/12/22/2.JPG)

    
    
    Input: grid = [[1,1,1],[1,1,1]]
    Output: 2
    Explanation: The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red. 
    Hence the total number of plots is 1 + 1 = 2.

Example 3


![](https://assets.leetcode.com/uploads/2021/12/22/3.JPG)

    
    
    Input: grid = [[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]]
    Output: 13
    Explanation: There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
    There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
    The total number of plots is 7 + 6 = 13.

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 10^5
  • grid[i][j] is either 0 or 1.

Solution

Method 1 – Dynamic Programming (DP) for Pyramid Heights

Intuition

A cell can be the apex of a pyramid of height h if the three cells directly below it can be the apex of pyramids of height at least h-1, and the current cell is fertile. We can use DP to compute the maximum height of a pyramid with apex at each cell, both for normal and inverse pyramids.

Approach

  1. For each cell, compute the maximum height of a pyramid with apex at (i, j) (top-down) using DP.
  2. For each cell, compute the maximum height of an inverse pyramid with apex at (i, j) (bottom-up) using DP.
  3. For each cell, add (height - 1) to the answer (since height 1 is not counted as a pyramid).
  4. Return the total count for both normal and inverse pyramids.

Code

C++
class Solution {
public:
    int countPyramids(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size(), ans = 0;
        auto dp = grid;
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n-1; ++j) {
                if (grid[i][j] && grid[i-1][j-1] && grid[i-1][j] && grid[i-1][j+1])
                    dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]}) + 1;
            }
        }
        for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) ans += dp[i][j] - 1;
        reverse(grid.begin(), grid.end());
        dp = grid;
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n-1; ++j) {
                if (grid[i][j] && grid[i-1][j-1] && grid[i-1][j] && grid[i-1][j+1])
                    dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]}) + 1;
            }
        }
        for (int i = 0; i < m; ++i) for (int j = 0; j < n; ++j) ans += dp[i][j] - 1;
        return ans;
    }
};
Go
func countPyramids(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    ans := 0
    dp := make([][]int, m)
    for i := range dp {
        dp[i] = append([]int(nil), grid[i]...)
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n-1; j++ {
            if grid[i][j] == 1 && grid[i-1][j-1] == 1 && grid[i-1][j] == 1 && grid[i-1][j+1] == 1 {
                dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i-1][j+1])) + 1
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            ans += dp[i][j] - 1
        }
    }
    // Inverse pyramids
    for i := range grid {
        for j := range grid[i] {
            dp[i][j] = grid[m-1-i][j]
        }
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n-1; j++ {
            if dp[i][j] == 1 && dp[i-1][j-1] == 1 && dp[i-1][j] == 1 && dp[i-1][j+1] == 1 {
                dp[i][j] = min(dp[i-1][j-1], min(dp[i-1][j], dp[i-1][j+1])) + 1
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            ans += dp[i][j] - 1
        }
    }
    return ans
}
func min(a, b int) int { if a < b { return a }; return b }
Java
class Solution {
    public int countPyramids(int[][] grid) {
        int m = grid.length, n = grid[0].length, ans = 0;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                dp[i][j] = grid[i][j];
        for (int i = 1; i < m; i++)
            for (int j = 1; j < n-1; j++)
                if (grid[i][j] == 1 && grid[i-1][j-1] == 1 && grid[i-1][j] == 1 && grid[i-1][j+1] == 1)
                    dp[i][j] = Math.min(Math.min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + 1;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                ans += dp[i][j] - 1;
        // Inverse pyramids
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                dp[i][j] = grid[m-1-i][j];
        for (int i = 1; i < m; i++)
            for (int j = 1; j < n-1; j++)
                if (dp[i][j] == 1 && dp[i-1][j-1] == 1 && dp[i-1][j] == 1 && dp[i-1][j+1] == 1)
                    dp[i][j] = Math.min(Math.min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + 1;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                ans += dp[i][j] - 1;
        return ans;
    }
}
Kotlin
class Solution {
    fun countPyramids(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        var ans = 0
        val dp = Array(m) { grid[it].clone() }
        for (i in 1 until m) {
            for (j in 1 until n-1) {
                if (grid[i][j] == 1 && grid[i-1][j-1] == 1 && grid[i-1][j] == 1 && grid[i-1][j+1] == 1)
                    dp[i][j] = minOf(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1
            }
        }
        for (i in 0 until m) for (j in 0 until n) ans += dp[i][j] - 1
        for (i in 0 until m) for (j in 0 until n) dp[i][j] = grid[m-1-i][j]
        for (i in 1 until m) {
            for (j in 1 until n-1) {
                if (dp[i][j] == 1 && dp[i-1][j-1] == 1 && dp[i-1][j] == 1 && dp[i-1][j+1] == 1)
                    dp[i][j] = minOf(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1
            }
        }
        for (i in 0 until m) for (j in 0 until n) ans += dp[i][j] - 1
        return ans
    }
}
Python
class Solution:
    def countPyramids(self, grid: list[list[int]]) -> int:
        m, n = len(grid), len(grid[0])
        ans = 0
        dp = [row[:] for row in grid]
        for i in range(1, m):
            for j in range(1, n-1):
                if grid[i][j] and grid[i-1][j-1] and grid[i-1][j] and grid[i-1][j+1]:
                    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1
        ans += sum(dp[i][j] - 1 for i in range(m) for j in range(n))
        grid = grid[::-1]
        dp = [row[:] for row in grid]
        for i in range(1, m):
            for j in range(1, n-1):
                if grid[i][j] and grid[i-1][j-1] and grid[i-1][j] and grid[i-1][j+1]:
                    dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1
        ans += sum(dp[i][j] - 1 for i in range(m) for j in range(n))
        return ans
Rust
impl Solution {
    pub fn count_pyramids(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut ans = 0;
        let mut dp = grid.clone();
        for i in 1..m {
            for j in 1..n-1 {
                if grid[i][j] == 1 && grid[i-1][j-1] == 1 && grid[i-1][j] == 1 && grid[i-1][j+1] == 1 {
                    dp[i][j] = dp[i-1][j-1].min(dp[i-1][j]).min(dp[i-1][j+1]) + 1;
                }
            }
        }
        for i in 0..m {
            for j in 0..n {
                ans += dp[i][j] - 1;
            }
        }
        let mut grid_rev = grid.clone();
        grid_rev.reverse();
        let mut dp = grid_rev.clone();
        for i in 1..m {
            for j in 1..n-1 {
                if grid_rev[i][j] == 1 && grid_rev[i-1][j-1] == 1 && grid_rev[i-1][j] == 1 && grid_rev[i-1][j+1] == 1 {
                    dp[i][j] = dp[i-1][j-1].min(dp[i-1][j]).min(dp[i-1][j+1]) + 1;
                }
            }
        }
        for i in 0..m {
            for j in 0..n {
                ans += dp[i][j] - 1;
            }
        }
        ans
    }
}
TypeScript
class Solution {
    countPyramids(grid: number[][]): number {
        const m = grid.length, n = grid[0].length;
        let ans = 0;
        let dp = grid.map(row => row.slice());
        for (let i = 1; i < m; i++) {
            for (let j = 1; j < n-1; j++) {
                if (grid[i][j] && grid[i-1][j-1] && grid[i-1][j] && grid[i-1][j+1])
                    dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1;
            }
        }
        for (let i = 0; i < m; i++) for (let j = 0; j < n; j++) ans += dp[i][j] - 1;
        grid.reverse();
        dp = grid.map(row => row.slice());
        for (let i = 1; i < m; i++) {
            for (let j = 1; j < n-1; j++) {
                if (grid[i][j] && grid[i-1][j-1] && grid[i-1][j] && grid[i-1][j+1])
                    dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + 1;
            }
        }
        for (let i = 0; i < m; i++) for (let j = 0; j < n; j++) ans += dp[i][j] - 1;
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(m * n), where m and n are the grid dimensions, for two DP passes.
  • 🧺 Space complexity: O(m * n), for the DP arrays.

Comments