Problem

Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return _thenumber of lattice points _that are present insideat least one circle.

Note:

  • A lattice point is a point with integer coordinates.
  • Points that lie on the circumference of a circle are also considered to be inside it.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


![](https://assets.leetcode.com/uploads/2022/03/02/exa-11.png)

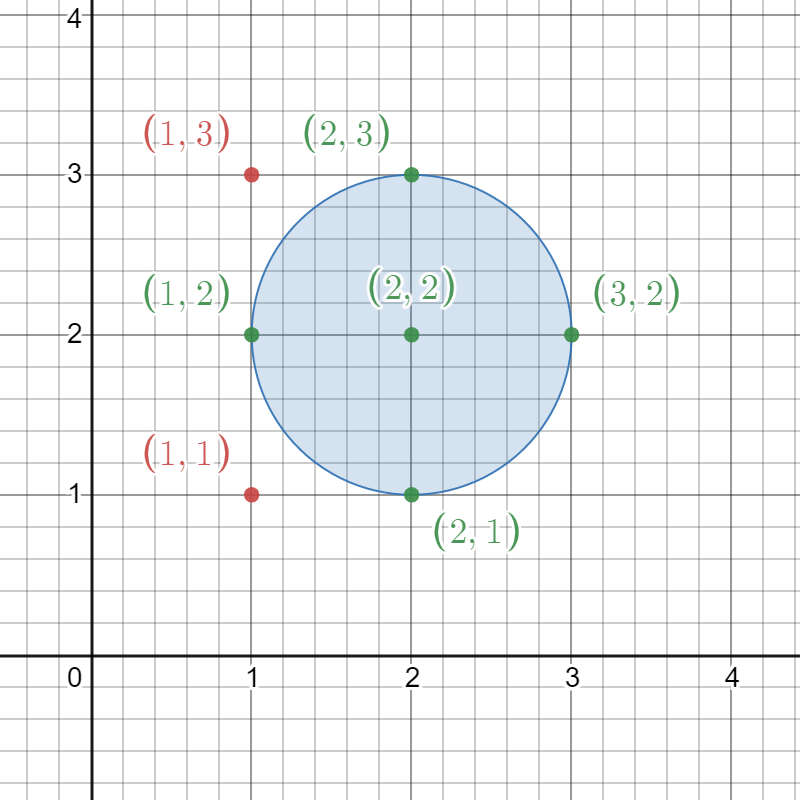
Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.

Example 2

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2022/03/02/exa-22.png)

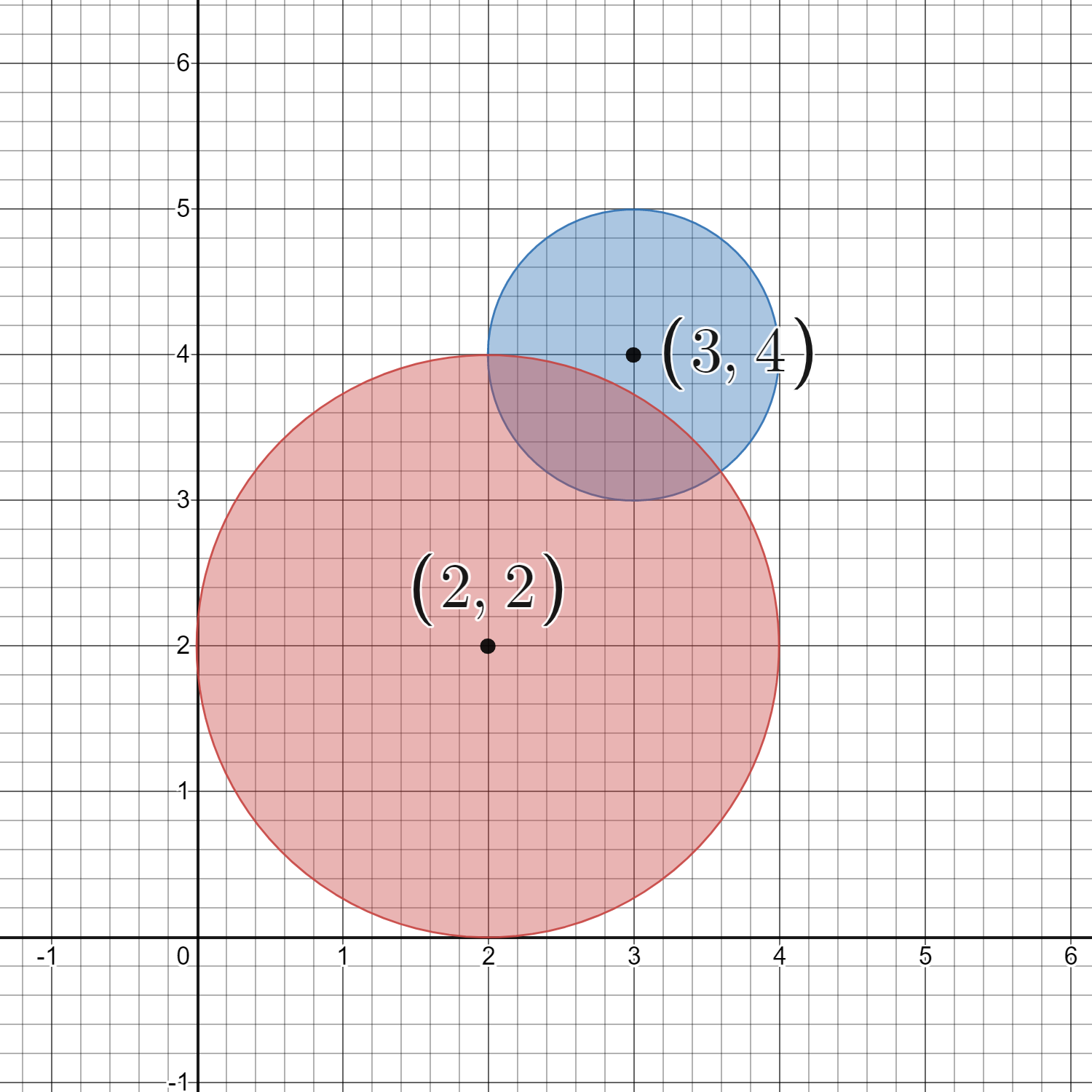
Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle. 
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).

Constraints

  • 1 <= circles.length <= 200
  • circles[i].length == 3
  • 1 <= xi, yi <= 100
  • 1 <= ri <= min(xi, yi)

Solution

Method 1 – Brute Force Enumeration

Intuition

For each circle, enumerate all integer points within its bounding box and check if they are inside or on the circle. Use a set to avoid counting duplicates from overlapping circles.

Approach

  1. Initialize an empty set to store unique lattice points.
  2. For each circle (xi, yi, ri):
    • Loop over all integer points (x, y) such that x in [xi-ri, xi+ri] and y in [yi-ri, yi+ri].
    • For each point, check if (x-xi)^2 + (y-yi)^2 <= ri^2.
    • If true, add (x, y) to the set.
  3. Return the size of the set.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int countLatticePoints(vector<vector<int>>& circles) {
        set<pair<int, int>> pts;
        for (auto& c : circles) {
            int x = c[0], y = c[1], r = c[2];
            for (int i = x - r; i <= x + r; ++i) {
                for (int j = y - r; j <= y + r; ++j) {
                    if ((i - x) * (i - x) + (j - y) * (j - y) <= r * r) {
                        pts.insert({i, j});
                    }
                }
            }
        }
        return pts.size();
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func countLatticePoints(circles [][]int) int {
    pts := make(map[[2]int]struct{})
    for _, c := range circles {
        x, y, r := c[0], c[1], c[2]
        for i := x - r; i <= x + r; i++ {
            for j := y - r; j <= y + r; j++ {
                if (i-x)*(i-x)+(j-y)*(j-y) <= r*r {
                    pts[[2]int{i, j}] = struct{}{}
                }
            }
        }
    }
    return len(pts)
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int countLatticePoints(int[][] circles) {
        Set<String> pts = new HashSet<>();
        for (int[] c : circles) {
            int x = c[0], y = c[1], r = c[2];
            for (int i = x - r; i <= x + r; ++i) {
                for (int j = y - r; j <= y + r; ++j) {
                    if ((i - x) * (i - x) + (j - y) * (j - y) <= r * r) {
                        pts.add(i + "," + j);
                    }
                }
            }
        }
        return pts.size();
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    fun countLatticePoints(circles: Array<IntArray>): Int {
        val pts = mutableSetOf<Pair<Int, Int>>() 
        for (c in circles) {
            val (x, y, r) = c
            for (i in x - r..x + r) {
                for (j in y - r..y + r) {
                    if ((i - x) * (i - x) + (j - y) * (j - y) <= r * r) {
                        pts.add(i to j)
                    }
                }
            }
        }
        return pts.size
    }
}
1
2
3
4
5
6
7
8
9

class Solution:
    def countLatticePoints(self, circles: list[list[int]]) -> int:
        pts: set[tuple[int, int]] = set()
        for x, y, r in circles:
            for i in range(x - r, x + r + 1):
                for j in range(y - r, y + r + 1):
                    if (i - x) ** 2 + (j - y) ** 2 <= r * r:
                        pts.add((i, j))
        return len(pts)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

use std::collections::HashSet;
impl Solution {
    pub fn count_lattice_points(circles: Vec<Vec<i32>>) -> i32 {
        let mut pts = HashSet::new();
        for c in circles {
            let (x, y, r) = (c[0], c[1], c[2]);
            for i in x - r..=x + r {
                for j in y - r..=y + r {
                    if (i - x).pow(2) + (j - y).pow(2) <= r.pow(2) {
                        pts.insert((i, j));
                    }
                }
            }
        }
        pts.len() as i32
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
    countLatticePoints(circles: number[][]): number {
        const pts = new Set<string>();
        for (const [x, y, r] of circles) {
            for (let i = x - r; i <= x + r; ++i) {
                for (let j = y - r; j <= y + r; ++j) {
                    if ((i - x) * (i - x) + (j - y) * (j - y) <= r * r) {
                        pts.add(`${i},${j}`);
                    }
                }
            }
        }
        return pts.size;
    }
}

Complexity

  • ⏰ Time complexity: O(m * r^2) where m is the number of circles and r is the maximum radius. For each circle, we check all points in its bounding box.
  • 🧺 Space complexity: O(N) where N is the number of unique lattice points covered by at least one circle.