Problem

Given the root of a binary tree, return the number of nodes where the value of the node is equal to theaverage of the values in its subtree.

Note:

  • The average of n elements is the sum of the n elements divided by n and rounded down to the nearest integer.
  • A subtree of root is a tree consisting of root and all of its descendants.

Examples

Example 1

1
2
3
4
5
6
7
8

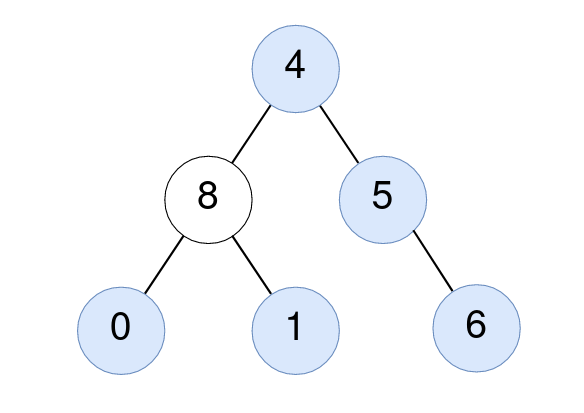
Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation: 
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.

Example 2

1
2
3

Input: root = [1]
Output: 1
Explanation: For the node with value 1: The average of its subtree is 1 / 1 = 1.

Constraints

  • The number of nodes in the tree is in the range [1, 1000].
  • 0 <= Node.val <= 1000

Solution

Method 1 – Postorder DFS with Subtree Sum and Count

Intuition

For each node, we need to know the sum and count of all nodes in its subtree. We can use postorder DFS to compute these values for every node efficiently.

Approach

  1. Traverse the tree in postorder (left, right, root).
  2. For each node, recursively get the sum and count of its left and right subtrees.
  3. Compute the sum and count for the current node (including itself).
  4. If the node’s value equals the integer average (sum // count), increment the answer.
  5. Return the answer after traversing the whole tree.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    int ans = 0;
    std::pair<int, int> dfs(TreeNode* node) {
        if (!node) return {0, 0};
        auto [ls, lc] = dfs(node->left);
        auto [rs, rc] = dfs(node->right);
        int s = ls + rs + node->val, c = lc + rc + 1;
        if (node->val == s / c) ans++;
        return {s, c};
    }
    int averageOfSubtree(TreeNode* root) {
        ans = 0;
        dfs(root);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}

func AverageOfSubtree(root *TreeNode) int {
    var ans int
    var dfs func(*TreeNode) (int, int)
    dfs = func(node *TreeNode) (int, int) {
        if node == nil {
            return 0, 0
        }
        ls, lc := dfs(node.Left)
        rs, rc := dfs(node.Right)
        s, c := ls+rs+node.Val, lc+rc+1
        if node.Val == s/c {
            ans++
        }
        return s, c
    }
    dfs(root)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    int ans = 0;
    private int[] dfs(TreeNode node) {
        if (node == null) return new int[]{0, 0};
        int[] l = dfs(node.left), r = dfs(node.right);
        int s = l[0] + r[0] + node.val, c = l[1] + r[1] + 1;
        if (node.val == s / c) ans++;
        return new int[]{s, c};
    }
    public int averageOfSubtree(TreeNode root) {
        ans = 0;
        dfs(root);
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

data class TreeNode(var `val`: Int, var left: TreeNode? = null, var right: TreeNode? = null)
class Solution {
    var ans = 0
    fun averageOfSubtree(root: TreeNode?): Int {
        ans = 0
        fun dfs(node: TreeNode?): Pair<Int, Int> {
            if (node == null) return 0 to 0
            val (ls, lc) = dfs(node.left)
            val (rs, rc) = dfs(node.right)
            val s = ls + rs + node.`val`
            val c = lc + rc + 1
            if (node.`val` == s / c) ans++
            return s to c
        }
        dfs(root)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def averageOfSubtree(self, root: TreeNode) -> int:
        self.ans = 0
        def dfs(node: TreeNode) -> tuple[int, int]:
            if not node:
                return 0, 0
            ls, lc = dfs(node.left)
            rs, rc = dfs(node.right)
            s, c = ls + rs + node.val, lc + rc + 1
            if node.val == s // c:
                self.ans += 1
            return s, c
        dfs(root)
        return self.ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

pub struct TreeNode {
    pub val: i32,
    pub left: Option<Box<TreeNode>>,
    pub right: Option<Box<TreeNode>>,
}

impl Solution {
    pub fn average_of_subtree(root: Option<Box<TreeNode>>) -> i32 {
        fn dfs(node: &Option<Box<TreeNode>>, ans: &mut i32) -> (i32, i32) {
            if let Some(n) = node {
                let (ls, lc) = dfs(&n.left, ans);
                let (rs, rc) = dfs(&n.right, ans);
                let s = ls + rs + n.val;
                let c = lc + rc + 1;
                if n.val == s / c { *ans += 1; }
                (s, c)
            } else {
                (0, 0)
            }
        }
        let mut ans = 0;
        dfs(&root, &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class TreeNode {
    val: number;
    left: TreeNode | null;
    right: TreeNode | null;
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = val ?? 0;
        this.left = left ?? null;
        this.right = right ?? null;
    }
}
class Solution {
    averageOfSubtree(root: TreeNode | null): number {
        let ans = 0;
        function dfs(node: TreeNode | null): [number, number] {
            if (!node) return [0, 0];
            const [ls, lc] = dfs(node.left);
            const [rs, rc] = dfs(node.right);
            const s = ls + rs + node.val, c = lc + rc + 1;
            if (node.val === Math.floor(s / c)) ans++;
            return [s, c];
        }
        dfs(root);
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes, since we visit each node once.
  • 🧺 Space complexity: O(h), where h is the height of the tree, due to recursion stack.