Count Number of Possible Root Nodes

Problem

Alice has an undirected tree with n nodes labeled from 0 to n - 1. The tree is represented as a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Alice wants Bob to find the root of the tree. She allows Bob to make several guesses about her tree. In one guess, he does the following:

• Chooses two distinct integers u and v such that there exists an edge [u, v] in the tree.
• He tells Alice that u is the parent of v in the tree.

Bob's guesses are represented by a 2D integer array guesses where guesses[j] = [uj, vj] indicates Bob guessed uj to be the parent of vj.

Alice being lazy, does not reply to each of Bob's guesses, but just says that at least k of his guesses are true.

Given the 2D integer arrays edges, guesses and the integer k, return thenumber of possible nodes that can be the root of Alice's tree. If there is no such tree, return 0.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2022/12/19/ex-1.png)

    
    
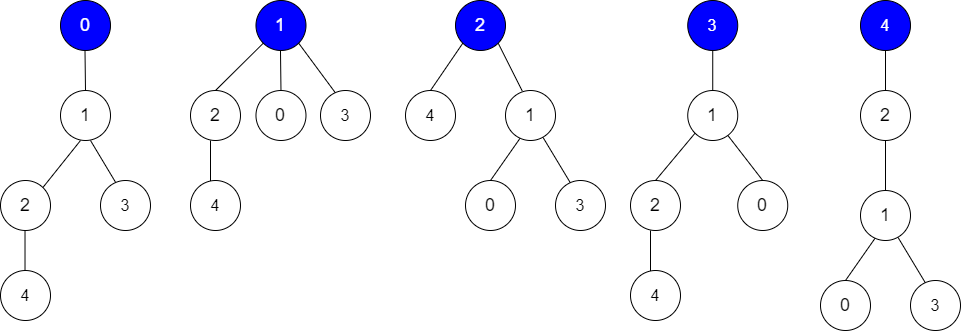
    Input: edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
    Output: 3
    Explanation: 
    Root = 0, correct guesses = [1,3], [0,1], [2,4]
    Root = 1, correct guesses = [1,3], [1,0], [2,4]
    Root = 2, correct guesses = [1,3], [1,0], [2,4]
    Root = 3, correct guesses = [1,0], [2,4]
    Root = 4, correct guesses = [1,3], [1,0]
    Considering 0, 1, or 2 as root node leads to 3 correct guesses.
    
    

Example 2

![](https://assets.leetcode.com/uploads/2022/12/19/ex-2.png)

    
    
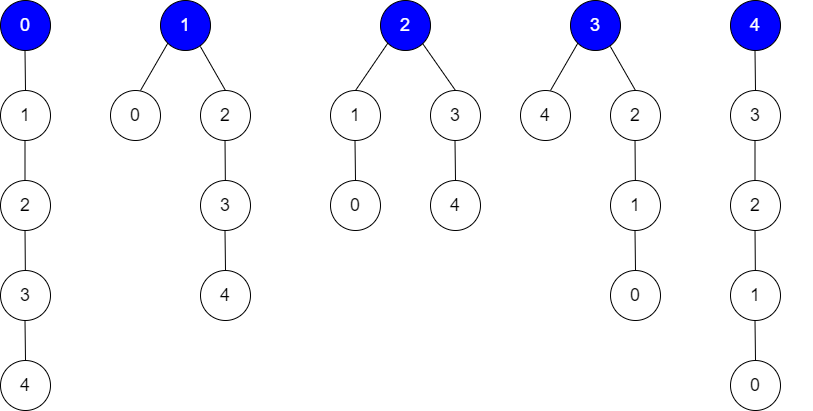
    Input: edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
    Output: 5
    Explanation: 
    Root = 0, correct guesses = [3,4]
    Root = 1, correct guesses = [1,0], [3,4]
    Root = 2, correct guesses = [1,0], [2,1], [3,4]
    Root = 3, correct guesses = [1,0], [2,1], [3,2], [3,4]
    Root = 4, correct guesses = [1,0], [2,1], [3,2]
    Considering any node as root will give at least 1 correct guess. 
    
    

Constraints

• edges.length == n - 1
• 2 <= n <= 10^5
• 1 <= guesses.length <= 10^5
• 0 <= ai, bi, uj, vj <= n - 1
• ai != bi
• uj != vj
• edges represents a valid tree.
• guesses[j] is an edge of the tree.
• guesses is unique.
• 0 <= k <= guesses.length

Solution

Method 1 – Rerooting DFS with Guess Counting

Intuition

We want to count how many nodes can be the root such that at least k guesses are correct. We can use DFS to count the number of correct guesses for one root, then reroot the tree and update the count efficiently for all possible roots.

Approach

1. Build the tree as an adjacency list.
2. Store all guesses in a set for O(1) lookup.
3. Use DFS to count the number of correct guesses if node 0 is the root.
4. Use rerooting DFS: for each child, update the count based on whether the guess (parent, child) is in the set, and recursively check all possible roots.
5. Count the number of roots where the number of correct guesses is at least k.

Code

C++

class Solution {
public:
    int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
        int n = edges.size() + 1;
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        set<pair<int,int>> guessSet;
        for (auto& gu : guesses) guessSet.insert({gu[0], gu[1]});
        int ans = 0, correct = 0;
        function<void(int,int)> dfs = [&](int u, int p) {
            for (int v : g[u]) if (v != p) {
                if (guessSet.count({u, v})) correct++;
                dfs(v, u);
            }
        };
        dfs(0, -1);
        function<void(int,int,int)> reroot = [&](int u, int p, int curr) {
            if (curr >= k) ans++;
            for (int v : g[u]) if (v != p) {
                int next = curr;
                if (guessSet.count({u, v})) next--;
                if (guessSet.count({v, u})) next++;
                reroot(v, u, next);
            }
        };
        reroot(0, -1, correct);
        return ans;
    }
};

Go

func RootCount(edges [][]int, guesses [][]int, k int) int {
    n := len(edges) + 1
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    guessSet := make(map[[2]int]struct{})
    for _, gu := range guesses {
        guessSet[[2]int{gu[0], gu[1]}] = struct{}{}
    }
    ans, correct := 0, 0
    var dfs func(int, int)
    dfs = func(u, p int) {
        for _, v := range g[u] {
            if v != p {
                if _, ok := guessSet[[2]int{u, v}]; ok {
                    correct++
                }
                dfs(v, u)
            }
        }
    }
    dfs(0, -1)
    var reroot func(int, int, int)
    reroot = func(u, p, curr int) {
        if curr >= k {
            ans++
        }
        for _, v := range g[u] {
            if v != p {
                next := curr
                if _, ok := guessSet[[2]int{u, v}]; ok {
                    next--
                }
                if _, ok := guessSet[[2]int{v, u}]; ok {
                    next++
                }
                reroot(v, u, next)
            }
        }
    }
    reroot(0, -1, correct)
    return ans
}

Java

class Solution {
    public int rootCount(int[][] edges, int[][] guesses, int k) {
        int n = edges.length + 1;
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        Set<String> guessSet = new HashSet<>();
        for (int[] gu : guesses) guessSet.add(gu[0] + "," + gu[1]);
        int[] correct = new int[1];
        dfs(0, -1, g, guessSet, correct);
        int[] ans = new int[1];
        reroot(0, -1, correct[0], g, guessSet, k, ans);
        return ans[0];
    }
    private void dfs(int u, int p, List<Integer>[] g, Set<String> guessSet, int[] correct) {
        for (int v : g[u]) if (v != p) {
            if (guessSet.contains(u + "," + v)) correct[0]++;
            dfs(v, u, g, guessSet, correct);
        }
    }
    private void reroot(int u, int p, int curr, List<Integer>[] g, Set<String> guessSet, int k, int[] ans) {
        if (curr >= k) ans[0]++;
        for (int v : g[u]) if (v != p) {
            int next = curr;
            if (guessSet.contains(u + "," + v)) next--;
            if (guessSet.contains(v + "," + u)) next++;
            reroot(v, u, next, g, guessSet, k, ans);
        }
    }
}

Kotlin

class Solution {
    fun rootCount(edges: Array<IntArray>, guesses: Array<IntArray>, k: Int): Int {
        val n = edges.size + 1
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val guessSet = mutableSetOf<Pair<Int, Int>>()
        for (gu in guesses) guessSet.add(gu[0] to gu[1])
        var correct = 0
        fun dfs(u: Int, p: Int) {
            for (v in g[u]) if (v != p) {
                if (guessSet.contains(u to v)) correct++
                dfs(v, v)
            }
        }
        dfs(0, -1)
        var ans = 0
        fun reroot(u: Int, p: Int, curr: Int) {
            if (curr >= k) ans++
            for (v in g[u]) if (v != p) {
                var next = curr
                if (guessSet.contains(u to v)) next--
                if (guessSet.contains(v to u)) next++
                reroot(v, u, next)
            }
        }
        reroot(0, -1, correct)
        return ans
    }
}

Python

class Solution:
    def rootCount(self, edges: list[list[int]], guesses: list[list[int]], k: int) -> int:
        from collections import defaultdict
        n = len(edges) + 1
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        guessSet = set((u, v) for u, v in guesses)
        correct = 0
        def dfs(u, p):
            nonlocal correct
            for v in g[u]:
                if v != p:
                    if (u, v) in guessSet:
                        correct += 1
                    dfs(v, u)
        dfs(0, -1)
        ans = 0
        def reroot(u, p, curr):
            nonlocal ans
            if curr >= k:
                ans += 1
            for v in g[u]:
                if v != p:
                    nextc = curr
                    if (u, v) in guessSet:
                        nextc -= 1
                    if (v, u) in guessSet:
                        nextc += 1
                    reroot(v, u, nextc)
        reroot(0, -1, correct)
        return ans

Rust

use std::collections::HashSet;
impl Solution {
    pub fn root_count(edges: Vec<Vec<i32>>, guesses: Vec<Vec<i32>>, k: i32) -> i32 {
        let n = edges.len() + 1;
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let guess_set: HashSet<(i32, i32)> = guesses.iter().map(|g| (g[0], g[1])).collect();
        let mut correct = 0;
        fn dfs(u: usize, p: i32, g: &Vec<Vec<usize>>, guess_set: &HashSet<(i32, i32)>, correct: &mut i32) {
            for &v in &g[u] {
                if v as i32 != p {
                    if guess_set.contains(&(u as i32, v as i32)) {
                        *correct += 1;
                    }
                    dfs(v, u as i32, g, guess_set, correct);
                }
            }
        }
        dfs(0, -1, &g, &guess_set, &mut correct);
        let mut ans = 0;
        fn reroot(u: usize, p: i32, curr: i32, g: &Vec<Vec<usize>>, guess_set: &HashSet<(i32, i32)>, k: i32, ans: &mut i32) {
            if curr >= k {
                *ans += 1;
            }
            for &v in &g[u] {
                if v as i32 != p {
                    let mut next = curr;
                    if guess_set.contains(&(u as i32, v as i32)) {
                        next -= 1;
                    }
                    if guess_set.contains(&(v as i32, u as i32)) {
                        next += 1;
                    }
                    reroot(v, u as i32, next, g, guess_set, k, ans);
                }
            }
        }
        reroot(0, -1, correct, &g, &guess_set, k, &mut ans);
        ans
    }
}

TypeScript

class Solution {
    rootCount(edges: number[][], guesses: number[][], k: number): number {
        const n = edges.length + 1;
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [a, b] of edges) {
            g[a].push(b);
            g[b].push(a);
        }
        const guessSet = new Set(guesses.map(([u, v]) => `${u},${v}`));
        let correct = 0;
        function dfs(u: number, p: number) {
            for (const v of g[u]) {
                if (v !== p) {
                    if (guessSet.has(`${u},${v}`)) correct++;
                    dfs(v, u);
                }
            }
        }
        dfs(0, -1);
        let ans = 0;
        function reroot(u: number, p: number, curr: number) {
            if (curr >= k) ans++;
            for (const v of g[u]) {
                if (v !== p) {
                    let next = curr;
                    if (guessSet.has(`${u},${v}`)) next--;
                    if (guessSet.has(`${v},${u}`)) next++;
                    reroot(v, u, next);
                }
            }
        }
        reroot(0, -1, correct);
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(n + m), where n is the number of nodes and m is the number of guesses, since we visit each node and guess once.
• 🧺 Space complexity: O(n + m), for storing the tree and guesses.