Problem

You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).

The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).

Return an integer arraycount of lengthpoints.length wherecount[j]_is the number of rectangles thatcontain the _jth point.

The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.

Examples

Example 1

1
2
3
4
5
6
7
8
9

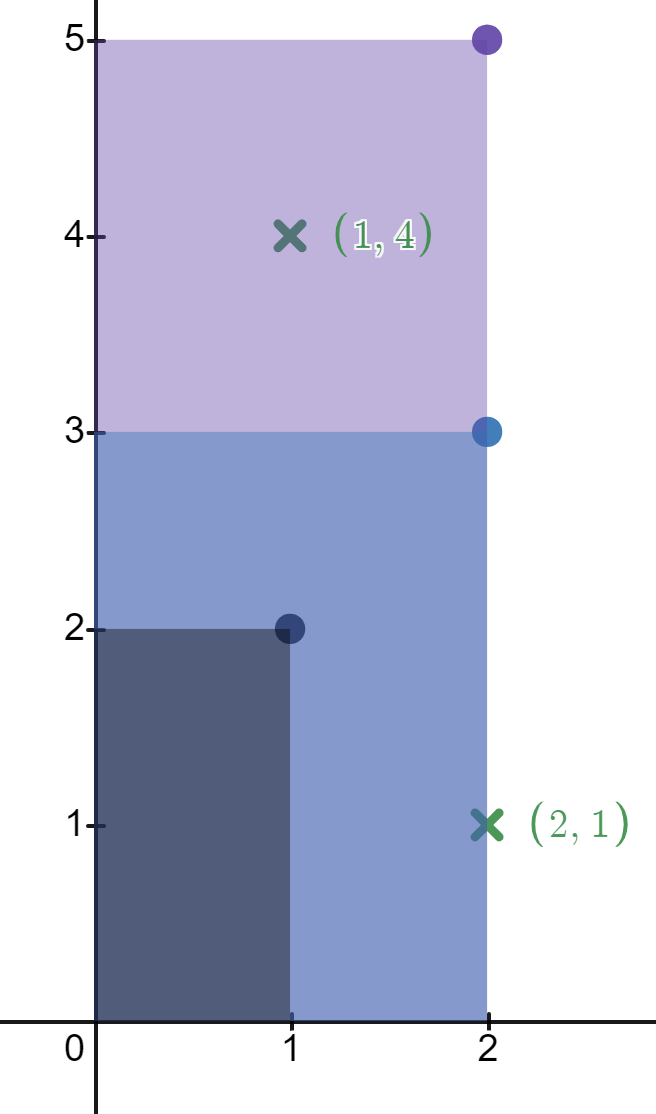
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
Output: [2,1]
Explanation: 
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return [2, 1].

Example 2

1
2
3
4
5
6
7
8

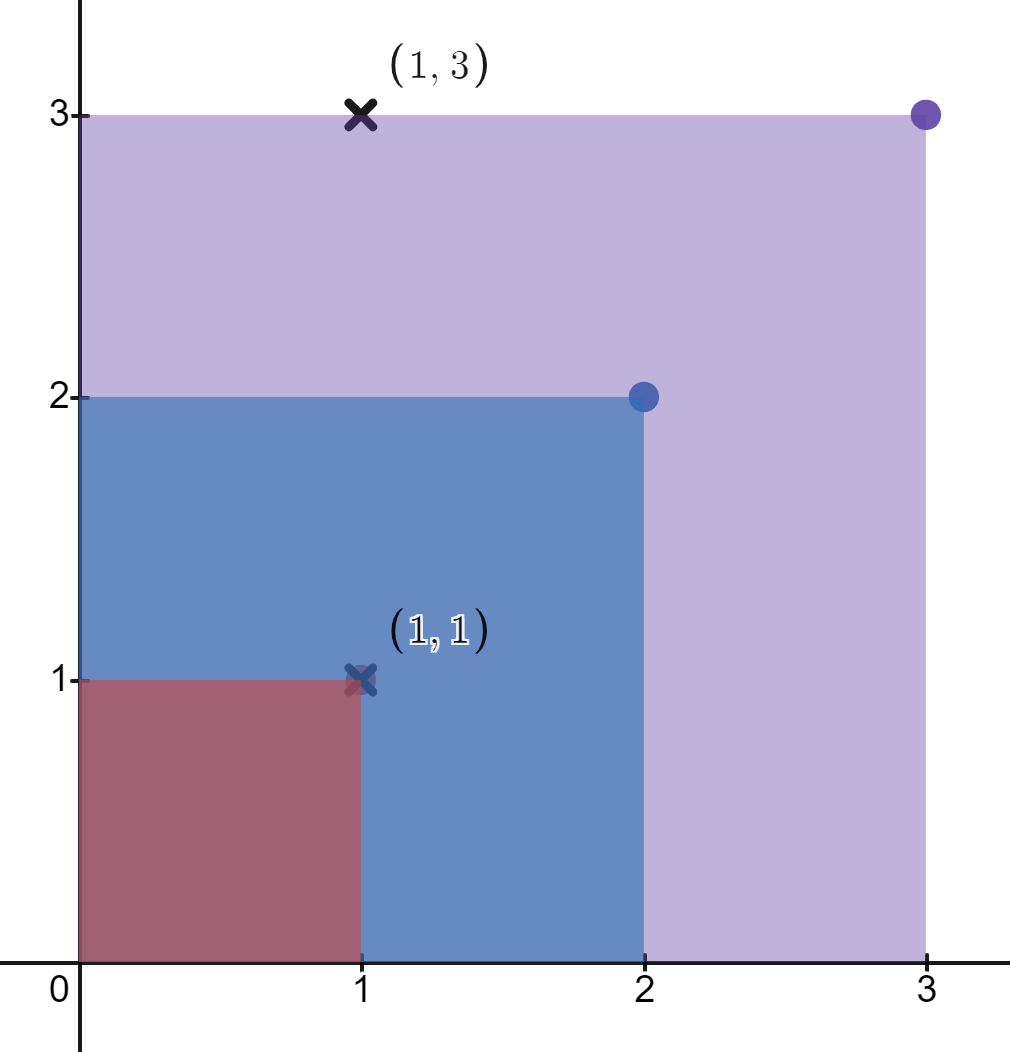
Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
Output: [1,3]
Explanation: The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return [1, 3].

Constraints

  • 1 <= rectangles.length, points.length <= 5 * 10^4
  • rectangles[i].length == points[j].length == 2
  • 1 <= li, xj <= 10^9
  • 1 <= hi, yj <= 100
  • All the rectangles are unique.
  • All the points are unique.

Solution

Method 1 – Sorting and Binary Search

Intuition

For each point, we want to count how many rectangles contain it. If we group rectangles by height and sort their lengths, we can efficiently count, for each point, how many rectangles have both length and height at least as large as the point’s coordinates using binary search.

Approach

  1. Group all rectangles by their height in a map from height to a list of lengths.
  2. For each height, sort the list of lengths.
  3. For each point, for all heights greater than or equal to the point’s y-coordinate, use binary search to count how many rectangles have length at least as large as the point’s x-coordinate.
  4. Sum these counts for all heights to get the answer for each point.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        map<int, vector<int>> h2l;
        for (auto& r : rectangles) h2l[r[1]].push_back(r[0]);
        for (auto& [h, v] : h2l) sort(v.begin(), v.end());
        vector<int> ans;
        for (auto& p : points) {
            int cnt = 0;
            for (auto it = h2l.lower_bound(p[1]); it != h2l.end(); ++it) {
                auto& v = it->second;
                cnt += v.end() - lower_bound(v.begin(), v.end(), p[0]);
            }
            ans.push_back(cnt);
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

func CountRectangles(rectangles [][]int, points [][]int) []int {
    h2l := map[int][]int{}
    for _, r := range rectangles {
        h2l[r[1]] = append(h2l[r[1]], r[0])
    }
    for h := range h2l {
        sort.Ints(h2l[h])
    }
    ans := make([]int, len(points))
    for i, p := range points {
        cnt := 0
        for h, v := range h2l {
            if h >= p[1] {
                idx := sort.SearchInts(v, p[0])
                cnt += len(v) - idx
            }
        }
        ans[i] = cnt
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    public int[] countRectangles(int[][] rectangles, int[][] points) {
        TreeMap<Integer, List<Integer>> h2l = new TreeMap<>();
        for (int[] r : rectangles) h2l.computeIfAbsent(r[1], x -> new ArrayList<>()).add(r[0]);
        for (List<Integer> v : h2l.values()) Collections.sort(v);
        int[] ans = new int[points.length];
        for (int i = 0; i < points.length; i++) {
            int cnt = 0;
            for (int h : h2l.tailMap(points[i][1]).keySet()) {
                List<Integer> v = h2l.get(h);
                int idx = Collections.binarySearch(v, points[i][0]);
                if (idx < 0) idx = -idx - 1;
                cnt += v.size() - idx;
            }
            ans[i] = cnt;
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
    fun countRectangles(rectangles: Array<IntArray>, points: Array<IntArray>): IntArray {
        val h2l = sortedMapOf<Int, MutableList<Int>>()
        for (r in rectangles) h2l.getOrPut(r[1]) { mutableListOf() }.add(r[0])
        for (v in h2l.values) v.sort()
        val ans = IntArray(points.size)
        for ((i, p) in points.withIndex()) {
            var cnt = 0
            for ((h, v) in h2l.tailMap(p[1])) {
                val idx = v.binarySearch(p[0]).let { if (it < 0) -it - 1 else it }
                cnt += v.size - idx
            }
            ans[i] = cnt
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution:
    def countRectangles(self, rectangles: list[list[int]], points: list[list[int]]) -> list[int]:
        from collections import defaultdict
        import bisect
        h2l = defaultdict(list)
        for l, h in rectangles:
            h2l[h].append(l)
        for v in h2l.values():
            v.sort()
        ans = []
        for x, y in points:
            cnt = 0
            for h in h2l:
                if h >= y:
                    v = h2l[h]
                    idx = bisect.bisect_left(v, x)
                    cnt += len(v) - idx
            ans.append(cnt)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

use std::collections::BTreeMap;
impl Solution {
    pub fn count_rectangles(rectangles: Vec<Vec<i32>>, points: Vec<Vec<i32>>) -> Vec<i32> {
        let mut h2l = BTreeMap::new();
        for r in rectangles {
            h2l.entry(r[1]).or_insert(vec![]).push(r[0]);
        }
        for v in h2l.values_mut() {
            v.sort();
        }
        let mut ans = vec![];
        for p in points {
            let mut cnt = 0;
            for (&h, v) in h2l.range(p[1]..=i32::MAX) {
                let idx = v.binary_search(&p[0]).unwrap_or_else(|x| x);
                cnt += v.len() - idx;
            }
            ans.push(cnt as i32);
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    countRectangles(rectangles: number[][], points: number[][]): number[] {
        const h2l = new Map<number, number[]>();
        for (const [l, h] of rectangles) {
            if (!h2l.has(h)) h2l.set(h, []);
            h2l.get(h)!.push(l);
        }
        for (const v of h2l.values()) v.sort((a, b) => a - b);
        const ans: number[] = [];
        for (const [x, y] of points) {
            let cnt = 0;
            for (const [h, v] of h2l.entries()) {
                if (h >= y) {
                    let l = 0, r = v.length;
                    while (l < r) {
                        const m = (l + r) >> 1;
                        if (v[m] < x) l = m + 1;
                        else r = m;
                    }
                    cnt += v.length - l;
                }
            }
            ans.push(cnt);
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O((n + m) * log n), where n is the number of rectangles and m is the number of points. For each point, we may check up to 100 heights, and for each, binary search in a sorted list of lengths.
  • 🧺 Space complexity: O(n), for storing the grouped rectangles.