problemmediumalgorithmsleetcode-2320leetcode 2320leetcode2320

Count Number of Ways to Place Houses

MediumUpdated: Jul 26, 2025
Practice on:
LeetCode

Problem

There is a street with n * 2 plots , where there are n plots on each side of the street. The plots on each side are numbered from 1 to n. On each plot, a house can be placed.

Return the number of ways houses can be placed such that no two houses are adjacent to each other on the same side of the street. Since the answer may be very large, return it modulo 10^9 + 7.

Note that if a house is placed on the ith plot on one side of the street, a house can also be placed on the ith plot on the other side of the street.

Examples

Example 1

Input: n = 1
Output: 4
Explanation: 
Possible arrangements:
1. All plots are empty.
2. A house is placed on one side of the street.
3. A house is placed on the other side of the street.
4. Two houses are placed, one on each side of the street.

Example 2


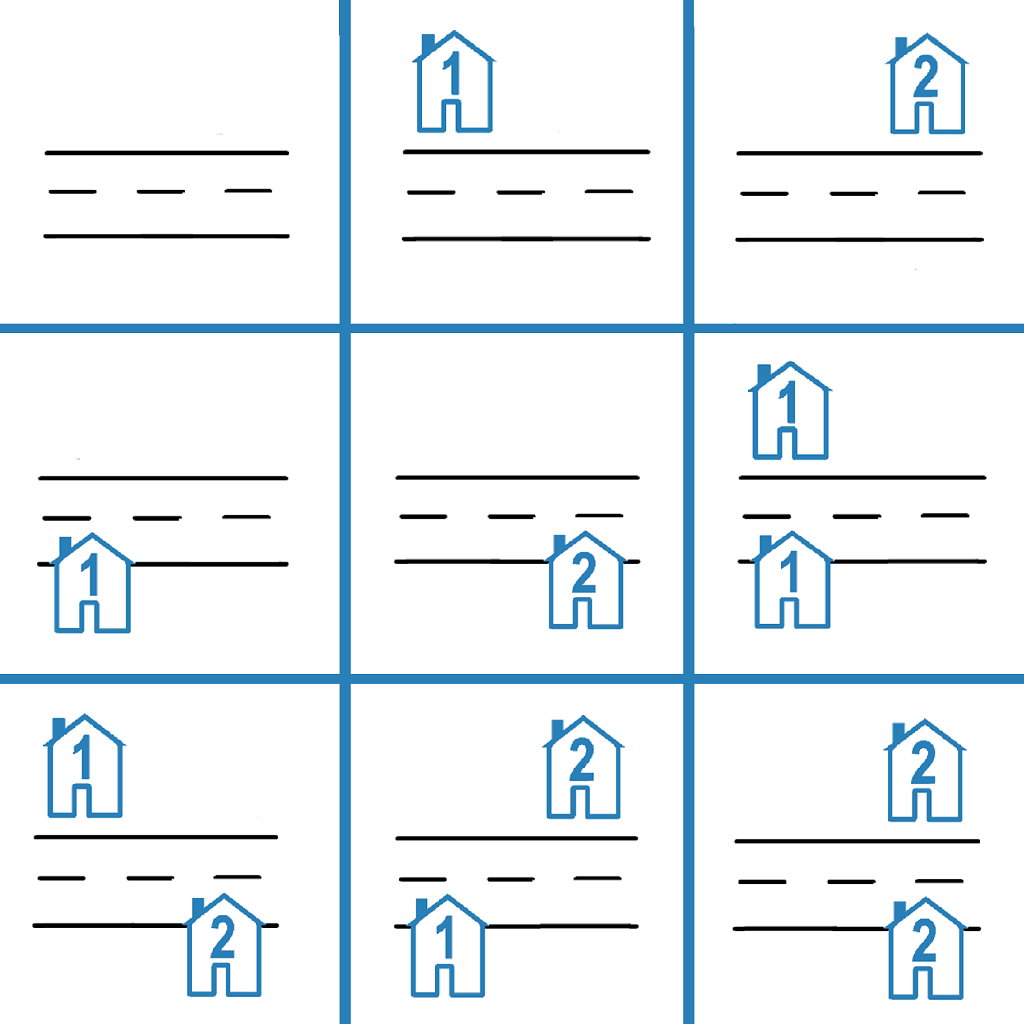
![](https://assets.leetcode.com/uploads/2022/05/12/arrangements.png)

Input: n = 2
Output: 9
Explanation: The 9 possible arrangements are shown in the diagram above.

Constraints

  • 1 <= n <= 10^4

Solution

Method 1 – Dynamic Programming with Fibonacci Relation

Intuition

The problem reduces to placing houses on a single row of n plots such that no two houses are adjacent. The number of ways to do this for one row is the (n+2)th Fibonacci number. Since both sides are independent, the answer is the square of this value.

Approach

  1. Let f[i] be the number of ways to place houses on a row of i plots with no two adjacent.
  2. The recurrence is: f[i] = f[i-1] + f[i-2] (either leave the last plot empty, or place a house and leave the previous empty).
  3. Initialize f[0] = 1, f[1] = 2 (empty or one house).
  4. Compute f[n] for the given n.
  5. The answer is (f[n] * f[n]) % MOD.

Code

C++
class Solution {
public:
    int countHousePlacements(int n) {
        const int MOD = 1e9+7;
        vector<long long> f(n+2, 0);
        f[0] = 1; f[1] = 2;
        for (int i = 2; i <= n; ++i) f[i] = (f[i-1] + f[i-2]) % MOD;
        return (f[n] * f[n]) % MOD;
    }
};
Go
func CountHousePlacements(n int) int {
    MOD := 1_000_000_007
    f := make([]int, n+2)
    f[0], f[1] = 1, 2
    for i := 2; i <= n; i++ {
        f[i] = (f[i-1] + f[i-2]) % MOD
    }
    return f[n] * f[n] % MOD
}
Java
class Solution {
    public int countHousePlacements(int n) {
        int MOD = 1_000_000_007;
        long[] f = new long[n+2];
        f[0] = 1; f[1] = 2;
        for (int i = 2; i <= n; i++) f[i] = (f[i-1] + f[i-2]) % MOD;
        return (int)(f[n] * f[n] % MOD);
    }
}
Kotlin
class Solution {
    fun countHousePlacements(n: Int): Int {
        val MOD = 1_000_000_007
        val f = LongArray(n+2)
        f[0] = 1; f[1] = 2
        for (i in 2..n) f[i] = (f[i-1] + f[i-2]) % MOD
        return ((f[n] * f[n]) % MOD).toInt()
    }
}
Python
class Solution:
    def countHousePlacements(self, n: int) -> int:
        MOD = 10**9 + 7
        f0, f1 = 1, 2
        for _ in range(2, n+1):
            f0, f1 = f1, (f0 + f1) % MOD
        return (f1 * f1) % MOD
Rust
impl Solution {
    pub fn count_house_placements(n: i32) -> i32 {
        let m = 1_000_000_007;
        let n = n as usize;
        let mut f = vec![0i64; n+2];
        f[0] = 1; f[1] = 2;
        for i in 2..=n {
            f[i] = (f[i-1] + f[i-2]) % m;
        }
        ((f[n] * f[n]) % m) as i32
    }
}
TypeScript
class Solution {
    countHousePlacements(n: number): number {
        const MOD = 1_000_000_007;
        let f0 = 1, f1 = 2;
        for (let i = 2; i <= n; i++) {
            [f0, f1] = [f1, (f0 + f1) % MOD];
        }
        return (f1 * f1) % MOD;
    }
}

Complexity

  • ⏰ Time complexity: O(n), since we compute the Fibonacci sequence up to n.
  • 🧺 Space complexity: O(n) (or O(1) if optimized), for storing the sequence or just two variables.

Comments