Count Pairs of Connectable Servers in a Weighted Tree Network
Problem
You are given an unrooted weighted tree with n vertices representing servers numbered from 0 to n - 1, an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional edge between vertices ai and bi of weight weighti. You are also given an integer signalSpeed.
Two servers a and b are connectable through a server c if:
a < b,a != candb != c.- The distance from
ctoais divisible bysignalSpeed. - The distance from
ctobis divisible bysignalSpeed. - The path from
ctoband the path fromctoado not share any edges.
Return an integer array count of length n where count[i] is thenumber of server pairs that are connectable through the server
i.
Examples
Example 1
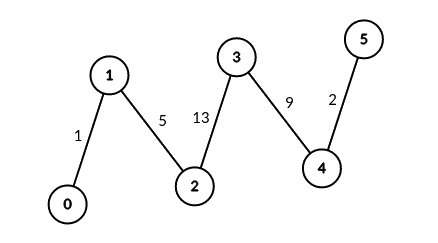
Input: edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
Output: [0,4,6,6,4,0]
Explanation: Since signalSpeed is 1, count[c] is equal to the number of pairs of paths that start at c and do not share any edges.
In the case of the given path graph, count[c] is equal to the number of servers to the left of c multiplied by the servers to the right of c.
Example 2
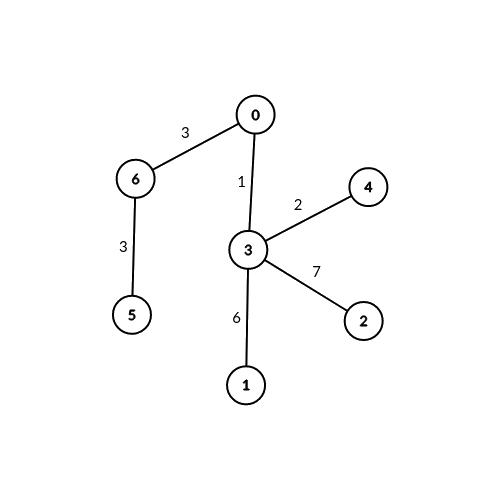
Input: edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
Output: [2,0,0,0,0,0,2]
Explanation: Through server 0, there are 2 pairs of connectable servers: (4, 5) and (4, 6).
Through server 6, there are 2 pairs of connectable servers: (4, 5) and (0, 5).
It can be shown that no two servers are connectable through servers other than 0 and 6.
Constraints
2 <= n <= 1000edges.length == n - 1edges[i].length == 30 <= ai, bi < nedges[i] = [ai, bi, weighti]1 <= weighti <= 10^61 <= signalSpeed <= 10^6- The input is generated such that
edgesrepresents a valid tree.
Solution
Method 1 – DFS and Path Counting by Subtree
Intuition
For each server c, the connectable pairs (a, b) must be in different subtrees of c, and the path from c to a and c to b must each have length divisible by signalSpeed. We can use DFS to count, for each subtree, the number of nodes at each distance mod signalSpeed, and then count valid pairs by combining counts from different subtrees.
Approach
- Build the tree as an adjacency list.
- For each node c (as the center), for each child subtree, use DFS to count the number of nodes at each distance mod signalSpeed.
- For each pair of subtrees, count the number of pairs (a, b) such that both distances are divisible by signalSpeed (i.e., both are 0 mod signalSpeed).
- For each c, sum the valid pairs from all pairs of subtrees.
- Return the answer for all c.
Code
C++
class Solution {
public:
vector<int> countPairsOfConnectableServers(int n, vector<vector<int>>& edges, int signalSpeed) {
vector<vector<pair<int,int>>> g(n);
for (auto& e : edges) {
g[e[0]].emplace_back(e[1], e[2]);
g[e[1]].emplace_back(e[0], e[2]);
}
vector<int> ans(n);
vector<int> cnt;
function<void(int,int,int)> dfs = [&](int u, int p, int d) {
if (d % signalSpeed == 0) cnt[0]++;
for (auto& [v, w] : g[u]) if (v != p) dfs(v, u, d + w);
};
for (int c = 0; c < n; ++c) {
vector<int> subtree_counts;
for (auto& [v, w] : g[c]) {
cnt = vector<int>(1, 0);
dfs(v, c, w);
subtree_counts.push_back(cnt[0]);
}
int total = 0;
for (int i = 0; i < subtree_counts.size(); ++i) {
for (int j = i+1; j < subtree_counts.size(); ++j) {
total += subtree_counts[i] * subtree_counts[j];
}
}
ans[c] = total;
}
return ans;
}
};
Go
func CountPairsOfConnectableServers(n int, edges [][]int, signalSpeed int) []int {
g := make([][][2]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], [2]int{e[1], e[2]})
g[e[1]] = append(g[e[1]], [2]int{e[0], e[2]})
}
ans := make([]int, n)
var dfs func(u, p, d int) int
dfs = func(u, p, d int) int {
cnt := 0
if d%signalSpeed == 0 {
cnt++
}
for _, vw := range g[u] {
v, w := vw[0], vw[1]
if v != p {
cnt += dfs(v, u, d+w)
}
}
return cnt
}
for c := 0; c < n; c++ {
var counts []int
for _, vw := range g[c] {
v, w := vw[0], vw[1]
counts = append(counts, dfs(v, c, w))
}
total := 0
for i := 0; i < len(counts); i++ {
for j := i+1; j < len(counts); j++ {
total += counts[i] * counts[j]
}
}
ans[c] = total
}
return ans
}
Java
class Solution {
public int[] countPairsOfConnectableServers(int n, int[][] edges, int signalSpeed) {
List<int[]>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(new int[]{e[1], e[2]});
g[e[1]].add(new int[]{e[0], e[2]});
}
int[] ans = new int[n];
for (int c = 0; c < n; c++) {
List<Integer> counts = new ArrayList<>();
for (int[] vw : g[c]) {
counts.add(dfs(g, vw[0], c, vw[1], signalSpeed));
}
int total = 0;
for (int i = 0; i < counts.size(); i++) {
for (int j = i+1; j < counts.size(); j++) {
total += counts.get(i) * counts.get(j);
}
}
ans[c] = total;
}
return ans;
}
private int dfs(List<int[]>[] g, int u, int p, int d, int signalSpeed) {
int cnt = d % signalSpeed == 0 ? 1 : 0;
for (int[] vw : g[u]) {
if (vw[0] != p) cnt += dfs(g, vw[0], u, d + vw[1], signalSpeed);
}
return cnt;
}
}
Kotlin
class Solution {
fun countPairsOfConnectableServers(n: Int, edges: Array<IntArray>, signalSpeed: Int): IntArray {
val g = Array(n) { mutableListOf<Pair<Int, Int>>() }
for (e in edges) {
g[e[0]].add(e[1] to e[2])
g[e[1]].add(e[0] to e[2])
}
val ans = IntArray(n)
fun dfs(u: Int, p: Int, d: Int): Int {
var cnt = if (d % signalSpeed == 0) 1 else 0
for ((v, w) in g[u]) if (v != p) cnt += dfs(v, u, d + w)
return cnt
}
for (c in 0 until n) {
val counts = mutableListOf<Int>()
for ((v, w) in g[c]) counts.add(dfs(v, c, w))
var total = 0
for (i in counts.indices) for (j in i+1 until counts.size) total += counts[i] * counts[j]
ans[c] = total
}
return ans
}
}
Python
class Solution:
def countPairsOfConnectableServers(self, n: int, edges: list[list[int]], signalSpeed: int) -> list[int]:
from collections import defaultdict
g = [[] for _ in range(n)]
for a, b, w in edges:
g[a].append((b, w))
g[b].append((a, w))
def dfs(u, p, d):
cnt = 1 if d % signalSpeed == 0 else 0
for v, w in g[u]:
if v != p:
cnt += dfs(v, u, d + w)
return cnt
ans = [0] * n
for c in range(n):
counts = [dfs(v, c, w) for v, w in g[c]]
total = 0
for i in range(len(counts)):
for j in range(i+1, len(counts)):
total += counts[i] * counts[j]
ans[c] = total
return ans
Rust
impl Solution {
pub fn count_pairs_of_connectable_servers(n: i32, edges: Vec<Vec<i32>>, signal_speed: i32) -> Vec<i32> {
let n = n as usize;
let mut g = vec![vec![]; n];
for e in &edges {
g[e[0] as usize].push((e[1] as usize, e[2]));
g[e[1] as usize].push((e[0] as usize, e[2]));
}
let mut ans = vec![0; n];
fn dfs(g: &Vec<Vec<(usize, i32)>>, u: usize, p: usize, d: i32, signal_speed: i32) -> i32 {
let mut cnt = if d % signal_speed == 0 { 1 } else { 0 };
for &(v, w) in &g[u] {
if v != p {
cnt += dfs(g, v, u, d + w, signal_speed);
}
}
cnt
}
for c in 0..n {
let mut counts = vec![];
for &(v, w) in &g[c] {
counts.push(dfs(&g, v, c, w, signal_speed));
}
let mut total = 0;
for i in 0..counts.len() {
for j in i+1..counts.len() {
total += counts[i] * counts[j];
}
}
ans[c] = total;
}
ans
}
}
TypeScript
class Solution {
countPairsOfConnectableServers(n: number, edges: number[][], signalSpeed: number): number[] {
const g: [number, number][][] = Array.from({length: n}, () => []);
for (const [a, b, w] of edges) {
g[a].push([b, w]);
g[b].push([a, w]);
}
function dfs(u: number, p: number, d: number): number {
let cnt = d % signalSpeed === 0 ? 1 : 0;
for (const [v, w] of g[u]) {
if (v !== p) cnt += dfs(v, u, d + w);
}
return cnt;
}
const ans = Array(n).fill(0);
for (let c = 0; c < n; c++) {
const counts = g[c].map(([v, w]) => dfs(v, c, w));
let total = 0;
for (let i = 0; i < counts.length; i++) {
for (let j = i+1; j < counts.length; j++) {
total += counts[i] * counts[j];
}
}
ans[c] = total;
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n^2), since for each node, we may traverse the whole tree in the worst case. - 🧺 Space complexity:
O(n), for the adjacency list and recursion stack.