Count Paths That Can Form a Palindrome in a Tree
Problem
You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to `n
- 1
. The tree is represented by a **0-indexed** arrayparentof sizen, whereparent[i]is the parent of nodei. Since node0is the root,parent[0] == -1`.
You are also given a string s of length n, where s[i] is the character assigned to the edge between i and parent[i]. s[0] can be ignored.
Return the number of pairs of nodes(u, v)such thatu < v and the characters assigned to edges on the path fromu tov can berearranged to form a palindrome.
A string is a palindrome when it reads the same backwards as forwards.
Examples
Example 1
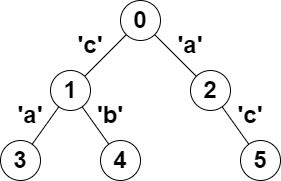
Input: parent = [-1,0,0,1,1,2], s = "acaabc"
Output: 8
Explanation: The valid pairs are:
- All the pairs (0,1), (0,2), (1,3), (1,4) and (2,5) result in one character which is always a palindrome.
- The pair (2,3) result in the string "aca" which is a palindrome.
- The pair (1,5) result in the string "cac" which is a palindrome.
- The pair (3,5) result in the string "acac" which can be rearranged into the palindrome "acca".
Example 2
Input: parent = [-1,0,0,0,0], s = "aaaaa"
Output: 10
Explanation: Any pair of nodes (u,v) where u < v is valid.
Constraints
n == parent.length == s.length1 <= n <= 10^50 <= parent[i] <= n - 1for alli >= 1parent[0] == -1parentrepresents a valid tree.sconsists of only lowercase English letters.
Solution
Method 1 – Bitmask and DFS
Intuition
A path can be rearranged into a palindrome if at most one character has an odd count. We can represent the parity of character counts along the path from the root to each node as a bitmask. For each node, the XOR of the bitmasks of two nodes gives the parity of the path between them. If the XOR result has at most one bit set, the path can form a palindrome.
Approach
- Build the tree from the parent array.
- Use DFS to compute the bitmask for each node (parity of character counts from root to node).
- Use a hash map to count the frequency of each bitmask.
- For each bitmask, count the number of pairs with the same bitmask (all even counts) and with bitmasks differing by one bit (one odd count).
- Sum all valid pairs and return the answer.
Code
C++
class Solution {
public:
long long countPalindromePaths(vector<int>& parent, string s) {
int n = parent.size();
vector<vector<int>> g(n);
for (int i = 1; i < n; ++i) g[parent[i]].push_back(i);
unordered_map<int, int> freq;
function<void(int, int)> dfs = [&](int u, int mask) {
mask ^= 1 << (s[u] - 'a');
freq[mask]++;
for (int v : g[u]) dfs(v, mask);
};
dfs(0, 0);
long long ans = 0;
for (auto& [mask, cnt] : freq) {
ans += 1LL * cnt * (cnt - 1) / 2;
for (int i = 0; i < 26; ++i) {
int m2 = mask ^ (1 << i);
if (freq.count(m2)) ans += 1LL * cnt * freq[m2] / 2;
}
}
return ans;
}
};
Go
func countPalindromePaths(parent []int, s string) int64 {
n := len(parent)
g := make([][]int, n)
for i := 1; i < n; i++ {
g[parent[i]] = append(g[parent[i]], i)
}
freq := map[int]int{}
var dfs func(int, int)
dfs = func(u, mask int) {
mask ^= 1 << (s[u] - 'a')
freq[mask]++
for _, v := range g[u] {
dfs(v, mask)
}
}
dfs(0, 0)
var ans int64
for mask, cnt := range freq {
ans += int64(cnt) * int64(cnt-1) / 2
for i := 0; i < 26; i++ {
m2 := mask ^ (1 << i)
if c2, ok := freq[m2]; ok {
ans += int64(cnt) * int64(c2) / 2
}
}
}
return ans
}
Java
class Solution {
public long countPalindromePaths(int[] parent, String s) {
int n = parent.length;
List<Integer>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int i = 1; i < n; i++) g[parent[i]].add(i);
Map<Integer, Integer> freq = new HashMap<>();
dfs(0, 0, s, g, freq);
long ans = 0;
for (var entry : freq.entrySet()) {
int mask = entry.getKey(), cnt = entry.getValue();
ans += 1L * cnt * (cnt - 1) / 2;
for (int i = 0; i < 26; i++) {
int m2 = mask ^ (1 << i);
if (freq.containsKey(m2)) ans += 1L * cnt * freq.get(m2) / 2;
}
}
return ans;
}
void dfs(int u, int mask, String s, List<Integer>[] g, Map<Integer, Integer> freq) {
mask ^= 1 << (s.charAt(u) - 'a');
freq.put(mask, freq.getOrDefault(mask, 0) + 1);
for (int v : g[u]) dfs(v, mask, s, g, freq);
}
}
Kotlin
class Solution {
fun countPalindromePaths(parent: IntArray, s: String): Long {
val n = parent.size
val g = Array(n) { mutableListOf<Int>() }
for (i in 1 until n) g[parent[i]].add(i)
val freq = mutableMapOf<Int, Int>()
fun dfs(u: Int, mask: Int) {
val m = mask xor (1 shl (s[u] - 'a'))
freq[m] = freq.getOrDefault(m, 0) + 1
for (v in g[u]) dfs(v, m)
}
dfs(0, 0)
var ans = 0L
for ((mask, cnt) in freq) {
ans += cnt.toLong() * (cnt - 1) / 2
for (i in 0 until 26) {
val m2 = mask xor (1 shl i)
freq[m2]?.let { ans += cnt.toLong() * it / 2 }
}
}
return ans
}
}
Python
class Solution:
def countPalindromePaths(self, parent: list[int], s: str) -> int:
from collections import defaultdict
n = len(parent)
g = [[] for _ in range(n)]
for i in range(1, n):
g[parent[i]].append(i)
freq = defaultdict(int)
def dfs(u: int, mask: int):
mask ^= 1 << (ord(s[u]) - ord('a'))
freq[mask] += 1
for v in g[u]:
dfs(v, mask)
dfs(0, 0)
ans = 0
for mask, cnt in freq.items():
ans += cnt * (cnt - 1) // 2
for i in range(26):
m2 = mask ^ (1 << i)
if m2 in freq:
ans += cnt * freq[m2] // 2
return ans
Rust
impl Solution {
pub fn count_palindrome_paths(parent: Vec<i32>, s: String) -> i64 {
use std::collections::HashMap;
let n = parent.len();
let mut g = vec![vec![]; n];
for i in 1..n {
g[parent[i] as usize].push(i);
}
let mut freq = HashMap::new();
fn dfs(u: usize, mask: i32, s: &[u8], g: &Vec<Vec<usize>>, freq: &mut HashMap<i32, i32>) {
let m = mask ^ (1 << (s[u] - b'a'));
*freq.entry(m).or_insert(0) += 1;
for &v in &g[u] {
dfs(v, m, s, g, freq);
}
}
dfs(0, 0, s.as_bytes(), &g, &mut freq);
let mut ans = 0i64;
for (&mask, &cnt) in &freq {
ans += cnt as i64 * (cnt - 1) as i64 / 2;
for i in 0..26 {
let m2 = mask ^ (1 << i);
if let Some(&c2) = freq.get(&m2) {
ans += cnt as i64 * c2 as i64 / 2;
}
}
}
ans
}
}
TypeScript
class Solution {
countPalindromePaths(parent: number[], s: string): number {
const n = parent.length;
const g: number[][] = Array.from({length: n}, () => []);
for (let i = 1; i < n; i++) g[parent[i]].push(i);
const freq: Record<number, number> = {};
function dfs(u: number, mask: number) {
mask ^= 1 << (s.charCodeAt(u) - 97);
freq[mask] = (freq[mask] || 0) + 1;
for (const v of g[u]) dfs(v, mask);
}
dfs(0, 0);
let ans = 0;
for (const maskStr in freq) {
const mask = Number(maskStr), cnt = freq[mask];
ans += cnt * (cnt - 1) / 2;
for (let i = 0; i < 26; i++) {
const m2 = mask ^ (1 << i);
if (freq[m2]) ans += cnt * freq[m2] / 2;
}
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n * 26), since we process each node and check 26 bitmasks for each. - 🧺 Space complexity:
O(n), for the frequency map and tree structure.