Problem

Given a 2D character matrix grid, where grid[i][j] is either 'X', 'Y', or '.', return the number of submatrices that contain:

  • grid[0][0]
  • an equal frequency of 'X' and 'Y'.
  • at least one 'X'.

Examples

Example 1

1
2
3
4
5
6
7
8


Input: grid = [["X","Y","."],["Y",".","."]]

Output: 3

Explanation:

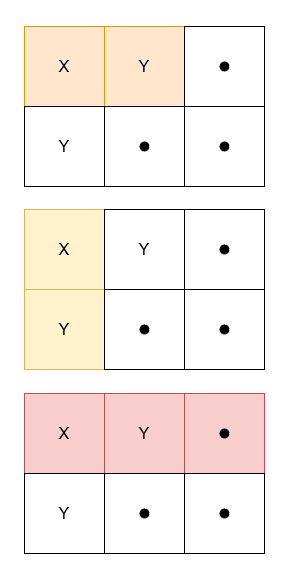**![](https://assets.leetcode.com/uploads/2024/06/07/examplems.png)**

Example 2

1
2
3
4
5
6
7
8


Input: grid = [["X","X"],["X","Y"]]

Output: 0

Explanation:

No submatrix has an equal frequency of `'X'` and `'Y'`.

Example 3

1
2
3
4
5
6
7
8


Input: grid = [[".","."],[".","."]]

Output: 0

Explanation:

No submatrix has at least one `'X'`.

Constraints

  • 1 <= grid.length, grid[i].length <= 1000
  • grid[i][j] is either 'X', 'Y', or '.'.

Solution

Method 1 – Prefix Sum with Hash Map

Intuition

We want to count all submatrices containing the top-left cell (0,0) that have an equal number of ‘X’ and ‘Y’ and at least one ‘X’. By using prefix sums, we can efficiently compute the difference between the number of ‘X’ and ‘Y’ in any submatrix starting at (0,0) and ending at (i,j).

Approach

  1. For each cell (i, j), compute two prefix sums:
    • The number of ‘X’ up to (i, j).
    • The number of ‘Y’ up to (i, j).
  2. For each possible bottom-right corner (i, j), consider all possible top-left corners (0, 0) to (i, j) (since the submatrix must include (0,0)).
  3. For each (i, j), use a hash map to count the number of previous columns where the difference between ‘X’ and ‘Y’ is the same, and at least one ‘X’ is present.
  4. For each row, use a running prefix sum and hash map to count valid submatrices ending at that row.
  5. Return the total count.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int countSubmatrices(vector<vector<char>>& grid) {
        int n = grid.size(), m = grid[0].size(), ans = 0;
        vector<vector<int>> px(n+1, vector<int>(m+1)), py(n+1, vector<int>(m+1));
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + (grid[i-1][j-1] == 'X');
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + (grid[i-1][j-1] == 'Y');
            }
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                for (int x = 1; x <= i; ++x) {
                    for (int y = 1; y <= j; ++y) {
                        if (x > 1 || y > 1) continue; // must include (0,0)
                        int cntX = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1];
                        int cntY = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1];
                        if (cntX == cntY && cntX > 0) ans++;
                    }
                }
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

type Solution struct{}
func (Solution) CountSubmatrices(grid [][]byte) int {
    n, m := len(grid), len(grid[0])
    px := make([][]int, n+1)
    py := make([][]int, n+1)
    for i := range px {
        px[i] = make([]int, m+1)
        py[i] = make([]int, m+1)
    }
    for i := 1; i <= n; i++ {
        for j := 1; j <= m; j++ {
            px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1]
            py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1]
            if grid[i-1][j-1] == 'X' {
                px[i][j]++
            }
            if grid[i-1][j-1] == 'Y' {
                py[i][j]++
            }
        }
    }
    ans := 0
    for i := 1; i <= n; i++ {
        for j := 1; j <= m; j++ {
            for x := 1; x <= i; x++ {
                for y := 1; y <= j; y++ {
                    if x > 1 || y > 1 {
                        continue
                    }
                    cntX := px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1]
                    cntY := py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1]
                    if cntX == cntY && cntX > 0 {
                        ans++
                    }
                }
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public int countSubmatrices(char[][] grid) {
        int n = grid.length, m = grid[0].length, ans = 0;
        int[][] px = new int[n+1][m+1], py = new int[n+1][m+1];
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + (grid[i-1][j-1] == 'X' ? 1 : 0);
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + (grid[i-1][j-1] == 'Y' ? 1 : 0);
            }
        }
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                for (int x = 1; x <= i; ++x) {
                    for (int y = 1; y <= j; ++y) {
                        if (x > 1 || y > 1) continue;
                        int cntX = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1];
                        int cntY = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1];
                        if (cntX == cntY && cntX > 0) ans++;
                    }
                }
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
    fun countSubmatrices(grid: Array<CharArray>): Int {
        val n = grid.size
        val m = grid[0].size
        val px = Array(n+1) { IntArray(m+1) }
        val py = Array(n+1) { IntArray(m+1) }
        for (i in 1..n) {
            for (j in 1..m) {
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + if (grid[i-1][j-1] == 'X') 1 else 0
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + if (grid[i-1][j-1] == 'Y') 1 else 0
            }
        }
        var ans = 0
        for (i in 1..n) {
            for (j in 1..m) {
                for (x in 1..i) {
                    for (y in 1..j) {
                        if (x > 1 || y > 1) continue
                        val cntX = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1]
                        val cntY = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1]
                        if (cntX == cntY && cntX > 0) ans++
                    }
                }
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def countSubmatrices(self, grid: list[list[str]]) -> int:
        n, m = len(grid), len(grid[0])
        px = [[0]*(m+1) for _ in range(n+1)]
        py = [[0]*(m+1) for _ in range(n+1)]
        for i in range(1, n+1):
            for j in range(1, m+1):
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + (grid[i-1][j-1] == 'X')
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + (grid[i-1][j-1] == 'Y')
        ans = 0
        for i in range(1, n+1):
            for j in range(1, m+1):
                for x in range(1, i+1):
                    for y in range(1, j+1):
                        if x > 1 or y > 1:
                            continue
                        cntX = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1]
                        cntY = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1]
                        if cntX == cntY and cntX > 0:
                            ans += 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

impl Solution {
    pub fn count_submatrices(grid: Vec<Vec<char>>) -> i32 {
        let n = grid.len();
        let m = grid[0].len();
        let mut px = vec![vec![0; m+1]; n+1];
        let mut py = vec![vec![0; m+1]; n+1];
        for i in 1..=n {
            for j in 1..=m {
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + if grid[i-1][j-1] == 'X' { 1 } else { 0 };
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + if grid[i-1][j-1] == 'Y' { 1 } else { 0 };
            }
        }
        let mut ans = 0;
        for i in 1..=n {
            for j in 1..=m {
                for x in 1..=i {
                    for y in 1..=j {
                        if x > 1 || y > 1 { continue; }
                        let cnt_x = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1];
                        let cnt_y = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1];
                        if cnt_x == cnt_y && cnt_x > 0 { ans += 1; }
                    }
                }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    countSubmatrices(grid: string[][]): number {
        const n = grid.length, m = grid[0].length;
        const px = Array.from({length: n+1}, () => Array(m+1).fill(0));
        const py = Array.from({length: n+1}, () => Array(m+1).fill(0));
        for (let i = 1; i <= n; ++i) {
            for (let j = 1; j <= m; ++j) {
                px[i][j] = px[i-1][j] + px[i][j-1] - px[i-1][j-1] + (grid[i-1][j-1] === 'X' ? 1 : 0);
                py[i][j] = py[i-1][j] + py[i][j-1] - py[i-1][j-1] + (grid[i-1][j-1] === 'Y' ? 1 : 0);
            }
        }
        let ans = 0;
        for (let i = 1; i <= n; ++i) {
            for (let j = 1; j <= m; ++j) {
                for (let x = 1; x <= i; ++x) {
                    for (let y = 1; y <= j; ++y) {
                        if (x > 1 || y > 1) continue;
                        const cntX = px[i][j] - px[x-1][j] - px[i][y-1] + px[x-1][y-1];
                        const cntY = py[i][j] - py[x-1][j] - py[i][y-1] + py[x-1][y-1];
                        if (cntX === cntY && cntX > 0) ans++;
                    }
                }
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n * m) for prefix sum calculation, but O(n * m) for the brute-force check (since we only check submatrices starting at (0,0)), so overall O(n * m).
  • 🧺 Space complexity: O(n * m) for prefix sum arrays.