Problem

You are given a 0-indexed integer matrix grid and an integer k.

Return thenumber of submatrices that contain the top-left element of the grid, and have a sum less than or equal tok.

Examples

Example 1

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2024/01/01/example1.png)

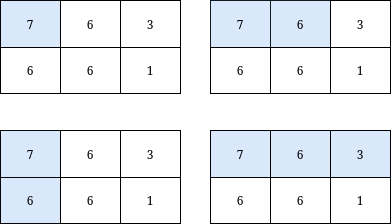
Input: grid = [[7,6,3],[6,6,1]], k = 18
Output: 4
Explanation: There are only 4 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 18.

Example 2

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2024/01/01/example21.png)

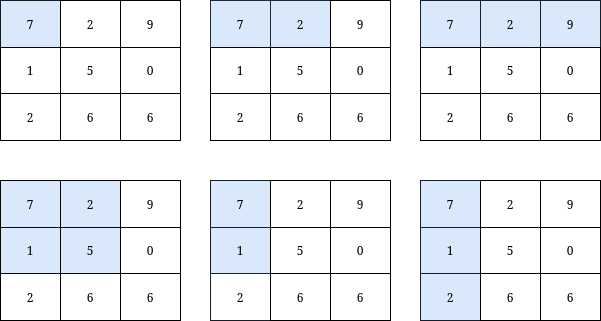
Input: grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20
Output: 6
Explanation: There are only 6 submatrices, shown in the image above, that contain the top-left element of grid, and have a sum less than or equal to 20.

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= n, m <= 1000
  • 0 <= grid[i][j] <= 1000
  • 1 <= k <= 10^9

Solution

Method 1 – Prefix Sum Brute Force

Intuition

We want to count all submatrices that start at the top-left (0,0) and end at (i,j) for all i, j, such that the sum of the submatrix is less than or equal to k. By precomputing prefix sums, we can quickly get the sum of any such submatrix.

Approach

  1. Compute a prefix sum matrix where each cell (i, j) contains the sum of the submatrix from (0,0) to (i,j).
  2. For every possible bottom-right corner (i, j), calculate the sum of the submatrix from (0,0) to (i,j) using the prefix sum.
  3. If the sum is less than or equal to k, increment the answer.
  4. Return the total count.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int countSubmatrices(vector<vector<int>>& grid, int k) {
        int n = grid.size(), m = grid[0].size(), ans = 0;
        vector<vector<int>> ps(n+1, vector<int>(m+1));
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1];
                if (ps[i][j] <= k) ans++;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

type Solution struct{}
func (Solution) CountSubmatrices(grid [][]int, k int) int {
    n, m := len(grid), len(grid[0])
    ps := make([][]int, n+1)
    for i := range ps {
        ps[i] = make([]int, m+1)
    }
    ans := 0
    for i := 1; i <= n; i++ {
        for j := 1; j <= m; j++ {
            ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1]
            if ps[i][j] <= k {
                ans++
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    public int countSubmatrices(int[][] grid, int k) {
        int n = grid.length, m = grid[0].length, ans = 0;
        int[][] ps = new int[n+1][m+1];
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1];
                if (ps[i][j] <= k) ans++;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
    fun countSubmatrices(grid: Array<IntArray>, k: Int): Int {
        val n = grid.size
        val m = grid[0].size
        val ps = Array(n+1) { IntArray(m+1) }
        var ans = 0
        for (i in 1..n) {
            for (j in 1..m) {
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1]
                if (ps[i][j] <= k) ans++
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution:
    def countSubmatrices(self, grid: list[list[int]], k: int) -> int:
        n, m = len(grid), len(grid[0])
        ps = [[0]*(m+1) for _ in range(n+1)]
        ans = 0
        for i in range(1, n+1):
            for j in range(1, m+1):
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1]
                if ps[i][j] <= k:
                    ans += 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

impl Solution {
    pub fn count_submatrices(grid: Vec<Vec<i32>>, k: i32) -> i32 {
        let n = grid.len();
        let m = grid[0].len();
        let mut ps = vec![vec![0; m+1]; n+1];
        let mut ans = 0;
        for i in 1..=n {
            for j in 1..=m {
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1];
                if ps[i][j] <= k {
                    ans += 1;
                }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    countSubmatrices(grid: number[][], k: number): number {
        const n = grid.length, m = grid[0].length;
        const ps = Array.from({length: n+1}, () => Array(m+1).fill(0));
        let ans = 0;
        for (let i = 1; i <= n; ++i) {
            for (let j = 1; j <= m; ++j) {
                ps[i][j] = grid[i-1][j-1] + ps[i-1][j] + ps[i][j-1] - ps[i-1][j-1];
                if (ps[i][j] <= k) ans++;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n * m) for prefix sum calculation and checking each submatrix starting at (0,0).
  • 🧺 Space complexity: O(n * m) for the prefix sum matrix.