Problem

There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [ui, vi] represents a bidirectional edge between cities ui and vi. There exists a unique path between each pair of cities. In other words, the cities form a tree.

A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.

For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.

Return an array of size n-1 where thedth ___element**(1-indexed)** is the number of subtrees in which the maximum distance between any two cities is equal to _d.

Notice that the distance between the two cities is the number of edges in the path between them.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


**![](https://assets.leetcode.com/uploads/2020/09/21/p1.png)**

    
    
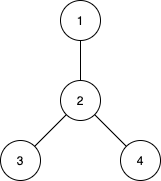    Input: n = 4, edges = [[1,2],[2,3],[2,4]]
    Output: [3,4,0]
    Explanation: The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
    The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
    No subtree has two nodes where the max distance between them is 3.

Example 2

1
2
3
4
5
6


    
    
    Input: n = 2, edges = [[1,2]]
    Output: [1]

Example 3

1
2
3
4
5
6


    
    
    Input: n = 3, edges = [[1,2],[2,3]]
    Output: [2,1]

Constraints

  • 2 <= n <= 15
  • edges.length == n-1
  • edges[i].length == 2
  • 1 <= ui, vi <= n
  • All pairs (ui, vi) are distinct.

Solution

Method 1 – Bitmask Enumeration and BFS

Intuition

Since n is small (≤ 15), we can enumerate all possible subsets of cities (using bitmasking). For each subset, if it forms a connected subtree, we can compute the maximum distance between any two cities in the subset using BFS. We count the number of subtrees for each possible maximum distance.

Approach

  1. Build the adjacency list for the tree.
  2. For each subset of cities (bitmask from 1 to 2^n - 1) with at least 2 cities:
    • Check if the subset is connected (using BFS or DFS).
    • If connected, for each node in the subset, run BFS to find the farthest node (diameter of the subtree).
    • The maximum distance found is the diameter for this subset.
    • Increment the count for this diameter.
  3. Return the counts for distances from 1 to n-1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

class Solution {
public:
    vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]-1].push_back(e[1]-1);
            g[e[1]-1].push_back(e[0]-1);
        }
        vector<int> ans(n-1);
        for (int mask = 1; mask < (1<<n); ++mask) {
            if (__builtin_popcount(mask) < 2) continue;
            vector<int> nodes;
            for (int i = 0; i < n; ++i) if (mask & (1<<i)) nodes.push_back(i);
            queue<int> q;
            vector<bool> vis(n);
            q.push(nodes[0]); vis[nodes[0]] = true;
            int cnt = 1;
            while (!q.empty()) {
                int u = q.front(); q.pop();
                for (int v : g[u]) {
                    if ((mask & (1<<v)) && !vis[v]) {
                        vis[v] = true; q.push(v); cnt++;
                    }
                }
            }
            if (cnt != nodes.size()) continue;
            int diam = 0;
            for (int u : nodes) {
                queue<pair<int,int>> q2;
                vector<bool> vis2(n);
                q2.push({u, 0}); vis2[u] = true;
                while (!q2.empty()) {
                    auto [v, d] = q2.front(); q2.pop();
                    diam = max(diam, d);
                    for (int w : g[v]) {
                        if ((mask & (1<<w)) && !vis2[w]) {
                            vis2[w] = true; q2.push({w, d+1});
                        }
                    }
                }
            }
            if (diam > 0) ans[diam-1]++;
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

type Solution struct{}
func (Solution) CountSubgraphsForEachDiameter(n int, edges [][]int) []int {
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]-1] = append(g[e[0]-1], e[1]-1)
        g[e[1]-1] = append(g[e[1]-1], e[0]-1)
    }
    ans := make([]int, n-1)
    for mask := 1; mask < (1<<n); mask++ {
        if bits.OnesCount(uint(mask)) < 2 {
            continue
        }
        nodes := []int{}
        for i := 0; i < n; i++ {
            if mask&(1<<i) != 0 {
                nodes = append(nodes, i)
            }
        }
        vis := make([]bool, n)
        q := []int{nodes[0]}
        vis[nodes[0]] = true
        cnt := 1
        for len(q) > 0 {
            u := q[0]; q = q[1:]
            for _, v := range g[u] {
                if mask&(1<<v) != 0 && !vis[v] {
                    vis[v] = true
                    q = append(q, v)
                    cnt++
                }
            }
        }
        if cnt != len(nodes) {
            continue
        }
        diam := 0
        for _, u := range nodes {
            vis2 := make([]bool, n)
            q2 := [][2]int{{u, 0}}
            vis2[u] = true
            for len(q2) > 0 {
                v, d := q2[0][0], q2[0][1]
                q2 = q2[1:]
                if d > diam {
                    diam = d
                }
                for _, w := range g[v] {
                    if mask&(1<<w) != 0 && !vis2[w] {
                        vis2[w] = true
                        q2 = append(q2, [2]int{w, d+1})
                    }
                }
            }
        }
        if diam > 0 {
            ans[diam-1]++
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

class Solution {
    public int[] countSubgraphsForEachDiameter(int n, int[][] edges) {
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]-1].add(e[1]-1);
            g[e[1]-1].add(e[0]-1);
        }
        int[] ans = new int[n-1];
        for (int mask = 1; mask < (1<<n); ++mask) {
            if (Integer.bitCount(mask) < 2) continue;
            List<Integer> nodes = new ArrayList<>();
            for (int i = 0; i < n; ++i) if ((mask & (1<<i)) != 0) nodes.add(i);
            Queue<Integer> q = new LinkedList<>();
            boolean[] vis = new boolean[n];
            q.add(nodes.get(0)); vis[nodes.get(0)] = true;
            int cnt = 1;
            while (!q.isEmpty()) {
                int u = q.poll();
                for (int v : g[u]) {
                    if ((mask & (1<<v)) != 0 && !vis[v]) {
                        vis[v] = true; q.add(v); cnt++;
                    }
                }
            }
            if (cnt != nodes.size()) continue;
            int diam = 0;
            for (int u : nodes) {
                Queue<int[]> q2 = new LinkedList<>();
                boolean[] vis2 = new boolean[n];
                q2.add(new int[]{u, 0}); vis2[u] = true;
                while (!q2.isEmpty()) {
                    int[] p = q2.poll();
                    int v = p[0], d = p[1];
                    diam = Math.max(diam, d);
                    for (int w : g[v]) {
                        if ((mask & (1<<w)) != 0 && !vis2[w]) {
                            vis2[w] = true; q2.add(new int[]{w, d+1});
                        }
                    }
                }
            }
            if (diam > 0) ans[diam-1]++;
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    fun countSubgraphsForEachDiameter(n: Int, edges: Array<IntArray>): IntArray {
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]-1].add(e[1]-1)
            g[e[1]-1].add(e[0]-1)
        }
        val ans = IntArray(n-1)
        for (mask in 1 until (1 shl n)) {
            if (Integer.bitCount(mask) < 2) continue
            val nodes = mutableListOf<Int>()
            for (i in 0 until n) if ((mask and (1 shl i)) != 0) nodes.add(i)
            val vis = BooleanArray(n)
            val q = ArrayDeque<Int>()
            q.add(nodes[0]); vis[nodes[0]] = true
            var cnt = 1
            while (q.isNotEmpty()) {
                val u = q.removeFirst()
                for (v in g[u]) {
                    if ((mask and (1 shl v)) != 0 && !vis[v]) {
                        vis[v] = true; q.add(v); cnt++
                    }
                }
            }
            if (cnt != nodes.size) continue
            var diam = 0
            for (u in nodes) {
                val vis2 = BooleanArray(n)
                val q2 = ArrayDeque<Pair<Int, Int>>()
                q2.add(u to 0); vis2[u] = true
                while (q2.isNotEmpty()) {
                    val (v, d) = q2.removeFirst()
                    diam = maxOf(diam, d)
                    for (w in g[v]) {
                        if ((mask and (1 shl w)) != 0 && !vis2[w]) {
                            vis2[w] = true; q2.add(w to d+1)
                        }
                    }
                }
            }
            if (diam > 0) ans[diam-1]++
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution:
    def countSubgraphsForEachDiameter(self, n: int, edges: list[list[int]]) -> list[int]:
        from collections import deque
        g = [[] for _ in range(n)]
        for u, v in edges:
            g[u-1].append(v-1)
            g[v-1].append(u-1)
        ans = [0] * (n-1)
        for mask in range(1, 1<<n):
            if bin(mask).count('1') < 2:
                continue
            nodes = [i for i in range(n) if (mask >> i) & 1]
            vis = [False] * n
            q = deque([nodes[0]])
            vis[nodes[0]] = True
            cnt = 1
            while q:
                u = q.popleft()
                for v in g[u]:
                    if (mask >> v) & 1 and not vis[v]:
                        vis[v] = True
                        q.append(v)
                        cnt += 1
            if cnt != len(nodes):
                continue
            diam = 0
            for u in nodes:
                vis2 = [False] * n
                q2 = deque([(u, 0)])
                vis2[u] = True
                while q2:
                    v, d = q2.popleft()
                    diam = max(diam, d)
                    for w in g[v]:
                        if (mask >> w) & 1 and not vis2[w]:
                            vis2[w] = True
                            q2.append((w, d+1))
            if diam > 0:
                ans[diam-1] += 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

impl Solution {
    pub fn count_subgraphs_for_each_diameter(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for e in edges.iter() {
            g[(e[0]-1) as usize].push((e[1]-1) as usize);
            g[(e[1]-1) as usize].push((e[0]-1) as usize);
        }
        let mut ans = vec![0; n-1];
        for mask in 1..(1<<n) {
            if mask.count_ones() < 2 { continue; }
            let nodes: Vec<_> = (0..n).filter(|&i| (mask>>i)&1 == 1).collect();
            let mut vis = vec![false; n];
            let mut q = std::collections::VecDeque::new();
            q.push_back(nodes[0]); vis[nodes[0]] = true;
            let mut cnt = 1;
            while let Some(u) = q.pop_front() {
                for &v in &g[u] {
                    if (mask>>v)&1 == 1 && !vis[v] {
                        vis[v] = true; q.push_back(v); cnt += 1;
                    }
                }
            }
            if cnt != nodes.len() { continue; }
            let mut diam = 0;
            for &u in &nodes {
                let mut vis2 = vec![false; n];
                let mut q2 = std::collections::VecDeque::new();
                q2.push_back((u, 0)); vis2[u] = true;
                while let Some((v, d)) = q2.pop_front() {
                    diam = diam.max(d);
                    for &w in &g[v] {
                        if (mask>>w)&1 == 1 && !vis2[w] {
                            vis2[w] = true; q2.push_back((w, d+1));
                        }
                    }
                }
            }
            if diam > 0 { ans[diam-1] += 1; }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    countSubgraphsForEachDiameter(n: number, edges: number[][]): number[] {
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [u, v] of edges) {
            g[u-1].push(v-1);
            g[v-1].push(u-1);
        }
        const ans = Array(n-1).fill(0);
        for (let mask = 1; mask < (1<<n); ++mask) {
            if (mask.toString(2).split('1').length-1 < 2) continue;
            const nodes = [];
            for (let i = 0; i < n; ++i) if ((mask>>i)&1) nodes.push(i);
            const vis = Array(n).fill(false);
            const q = [nodes[0]];
            vis[nodes[0]] = true;
            let cnt = 1;
            while (q.length) {
                const u = q.shift()!;
                for (const v of g[u]) {
                    if ((mask>>v)&1 && !vis[v]) {
                        vis[v] = true; q.push(v); cnt++;
                    }
                }
            }
            if (cnt !== nodes.length) continue;
            let diam = 0;
            for (const u of nodes) {
                const vis2 = Array(n).fill(false);
                const q2: [number, number][] = [[u, 0]];
                vis2[u] = true;
                while (q2.length) {
                    const [v, d] = q2.shift()!;
                    diam = Math.max(diam, d);
                    for (const w of g[v]) {
                        if ((mask>>w)&1 && !vis2[w]) {
                            vis2[w] = true; q2.push([w, d+1]);
                        }
                    }
                }
            }
            if (diam > 0) ans[diam-1]++;
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(3^n * n^2), since for each subset (2^n), we check connectivity and diameter (each O(n^2)).
  • 🧺 Space complexity: O(n^2) for adjacency and visited arrays.