Count the Number of Good Nodes
MediumUpdated: Aug 2, 2025
Practice on:
Problem
There is an undirected tree with n nodes labeled from 0 to n - 1, and rooted at node 0. You are given a 2D integer array edges of length `n
- 1
, whereedges[i] = [ai, bi]indicates that there is an edge between nodesaiandbi` in the tree.
A node is good if all the subtrees rooted at its children have the same size.
Return the number of good nodes in the given tree.
A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.
Examples
Example 1
Input: edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
Output: 7
Explanation:
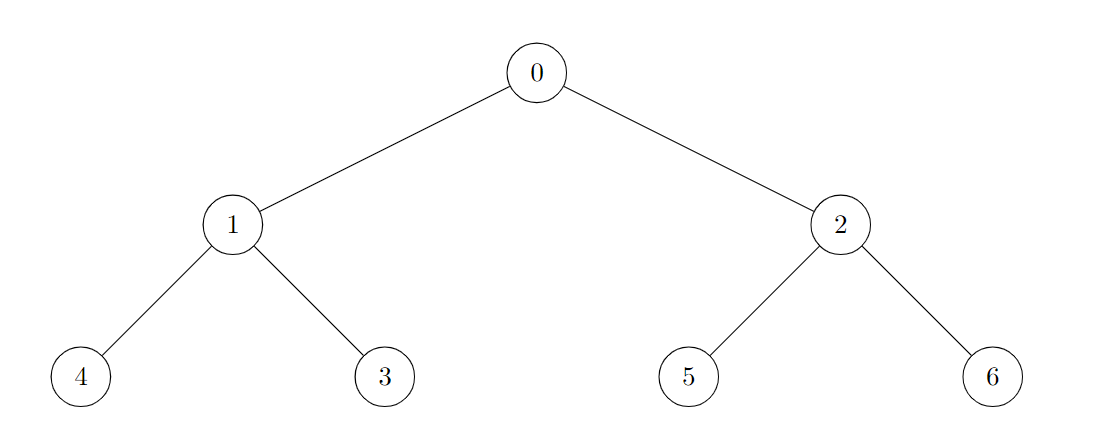
All of the nodes of the given tree are good.
Example 2
Input: edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]
Output: 6
Explanation:
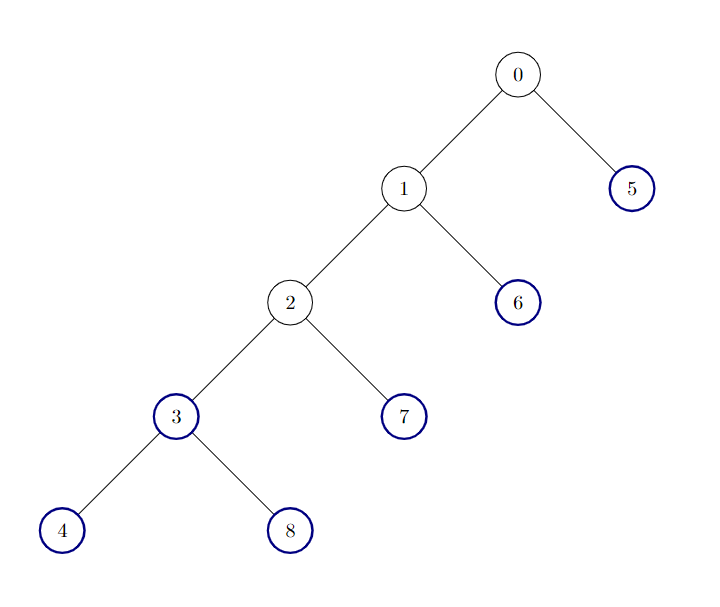
There are 6 good nodes in the given tree. They are colored in the image above.
Example 3
Input: edges =
[[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]
Output: 12
Explanation:
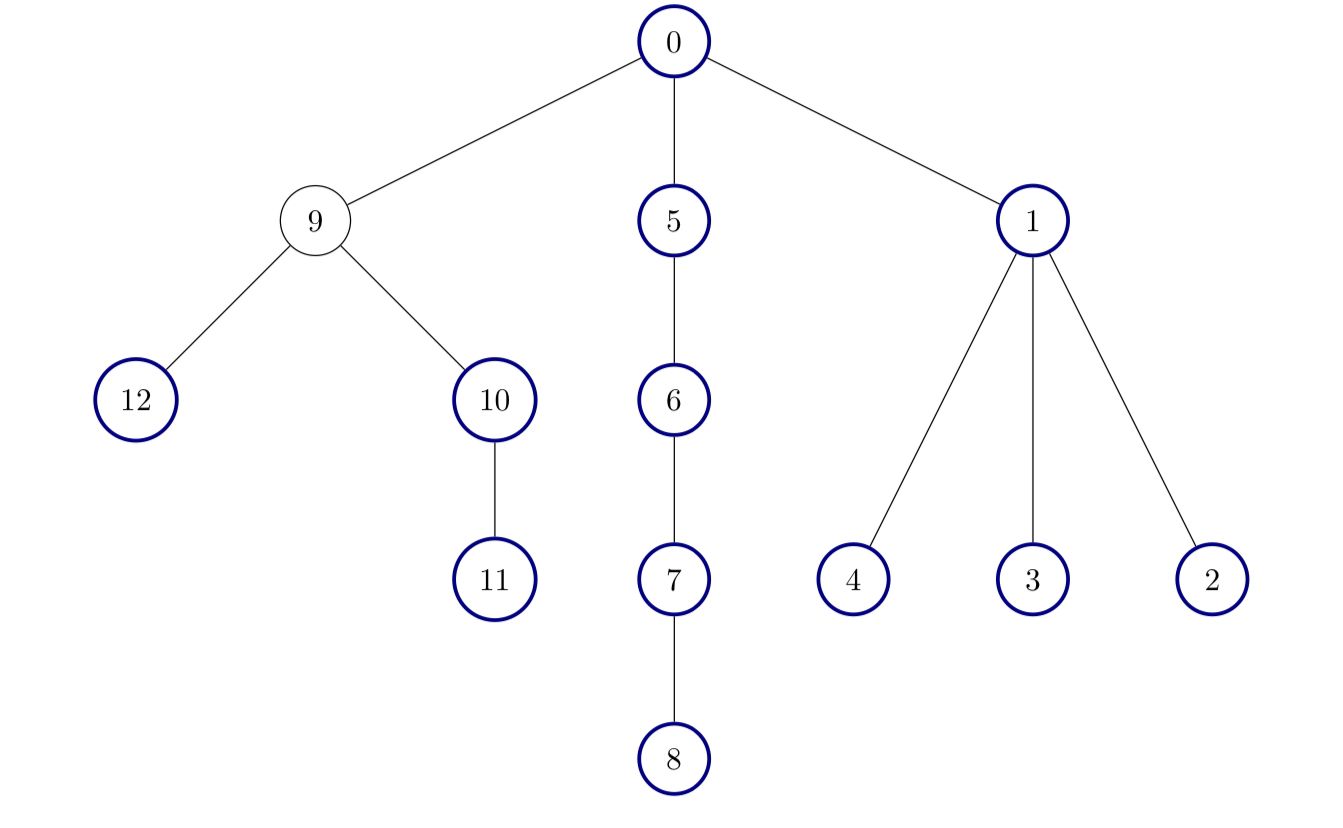
All nodes except node 9 are good.
Constraints
2 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < n- The input is generated such that
edgesrepresents a valid tree.
Solution
Method 1 – DFS to Compute Subtree Sizes
Intuition
A node is good if all its children have subtrees of the same size. We can use DFS to compute the size of each subtree and check for each node if all its children have the same subtree size.
Approach
- Build the adjacency list for the tree.
- Use DFS to compute the size of the subtree rooted at each node.
- For each node, collect the sizes of all its children’s subtrees.
- If all children’s subtree sizes are equal (or the node is a leaf), count the node as good.
- Return the total number of good nodes.
Code
C++
class Solution {
public:
int countGoodNodes(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<int> sz(n);
int ans = 0;
function<void(int,int)> dfs = [&](int u, int p) {
sz[u] = 1;
vector<int> child_sizes;
for (int v : g[u]) if (v != p) {
dfs(v, u);
sz[u] += sz[v];
child_sizes.push_back(sz[v]);
}
if (child_sizes.empty() || all_of(child_sizes.begin(), child_sizes.end(), [&](int x){return x == child_sizes[0];}))
ans++;
};
dfs(0, -1);
return ans;
}
};
Go
type Solution struct{}
func (Solution) CountGoodNodes(n int, edges [][]int) int {
g := make([][]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], e[1])
g[e[1]] = append(g[e[1]], e[0])
}
sz := make([]int, n)
var ans int
var dfs func(u, p int)
dfs = func(u, p int) {
sz[u] = 1
childSizes := []int{}
for _, v := range g[u] {
if v != p {
dfs(v, u)
sz[u] += sz[v]
childSizes = append(childSizes, sz[v])
}
}
good := true
for i := 1; i < len(childSizes); i++ {
if childSizes[i] != childSizes[0] {
good = false
break
}
}
if len(childSizes) == 0 || good {
ans++
}
}
dfs(0, -1)
return ans
}
Java
class Solution {
public int countGoodNodes(int n, int[][] edges) {
List<Integer>[] g = new List[n];
for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
}
int[] sz = new int[n];
int[] ans = new int[1];
dfs(0, -1, g, sz, ans);
return ans[0];
}
void dfs(int u, int p, List<Integer>[] g, int[] sz, int[] ans) {
sz[u] = 1;
List<Integer> childSizes = new ArrayList<>();
for (int v : g[u]) if (v != p) {
dfs(v, u, g, sz, ans);
sz[u] += sz[v];
childSizes.add(sz[v]);
}
boolean good = true;
for (int i = 1; i < childSizes.size(); i++) {
if (!childSizes.get(i).equals(childSizes.get(0))) {
good = false;
break;
}
}
if (childSizes.isEmpty() || good) ans[0]++;
}
}
Kotlin
class Solution {
fun countGoodNodes(n: Int, edges: Array<IntArray>): Int {
val g = Array(n) { mutableListOf<Int>() }
for (e in edges) {
g[e[0]].add(e[1])
g[e[1]].add(e[0])
}
val sz = IntArray(n)
var ans = 0
fun dfs(u: Int, p: Int) {
sz[u] = 1
val childSizes = mutableListOf<Int>()
for (v in g[u]) if (v != p) {
dfs(v, u)
sz[u] += sz[v]
childSizes.add(sz[v])
}
if (childSizes.isEmpty() || childSizes.all { it == childSizes[0] }) ans++
}
dfs(0, -1)
return ans
}
}
Python
class Solution:
def countGoodNodes(self, n: int, edges: list[list[int]]) -> int:
g = [[] for _ in range(n)]
for a, b in edges:
g[a].append(b)
g[b].append(a)
sz = [0] * n
ans = 0
def dfs(u: int, p: int) -> None:
nonlocal ans
sz[u] = 1
child_sizes = []
for v in g[u]:
if v != p:
dfs(v, u)
sz[u] += sz[v]
child_sizes.append(sz[v])
if not child_sizes or all(x == child_sizes[0] for x in child_sizes):
ans += 1
dfs(0, -1)
return ans
Rust
impl Solution {
pub fn count_good_nodes(n: i32, edges: Vec<Vec<i32>>) -> i32 {
let n = n as usize;
let mut g = vec![vec![]; n];
for e in edges.iter() {
g[e[0] as usize].push(e[1] as usize);
g[e[1] as usize].push(e[0] as usize);
}
let mut sz = vec![0; n];
let mut ans = 0;
fn dfs(u: usize, p: i32, g: &Vec<Vec<usize>>, sz: &mut Vec<i32>, ans: &mut i32) {
sz[u] = 1;
let mut child_sizes = vec![];
for &v in &g[u] {
if v as i32 != p {
dfs(v, u as i32, g, sz, ans);
sz[u] += sz[v];
child_sizes.push(sz[v]);
}
}
if child_sizes.is_empty() || child_sizes.iter().all(|&x| x == child_sizes[0]) {
*ans += 1;
}
}
dfs(0, -1, &g, &mut sz, &mut ans);
ans
}
}
TypeScript
class Solution {
countGoodNodes(n: number, edges: number[][]): number {
const g: number[][] = Array.from({length: n}, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
const sz = Array(n).fill(0);
let ans = 0;
function dfs(u: number, p: number) {
sz[u] = 1;
const childSizes: number[] = [];
for (const v of g[u]) if (v !== p) {
dfs(v, u);
sz[u] += sz[v];
childSizes.push(sz[v]);
}
if (childSizes.length === 0 || childSizes.every(x => x === childSizes[0])) ans++;
}
dfs(0, -1);
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n), where n is the number of nodes, since we visit each node once. - 🧺 Space complexity:
O(n), for the adjacency list and subtree sizes.