Problem

You are given three positive integers n, x, and y.

In a city, there exist houses numbered 1 to n connected by n streets. There is a street connecting the house numbered i with the house numbered `i

  • 1for all1 <= i <= n - 1. An additional street connects the house numberedxwith the house numberedy`.

For each k, such that 1 <= k <= n, you need to find the number of pairs of houses (house1, house2) such that the minimum number of streets that need to be traveled to reach house2 from house1 is k.

Return _a1-indexed array _result of lengthn whereresult[k]_represents thetotal number of pairs of houses such that the minimum streets required to reach one house from the other is _k.

Note that x and y can be equal.

Examples

Example 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


![](https://assets.leetcode.com/uploads/2023/12/20/example2.png)

    
    
    Input: n = 3, x = 1, y = 3
    Output: [6,0,0]
    Explanation: Let's look at each pair of houses:
    - For the pair (1, 2), we can go from house 1 to house 2 directly.
    - For the pair (2, 1), we can go from house 2 to house 1 directly.
    - For the pair (1, 3), we can go from house 1 to house 3 directly.
    - For the pair (3, 1), we can go from house 3 to house 1 directly.
    - For the pair (2, 3), we can go from house 2 to house 3 directly.
    - For the pair (3, 2), we can go from house 3 to house 2 directly.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


![](https://assets.leetcode.com/uploads/2023/12/20/example3.png)

    
    
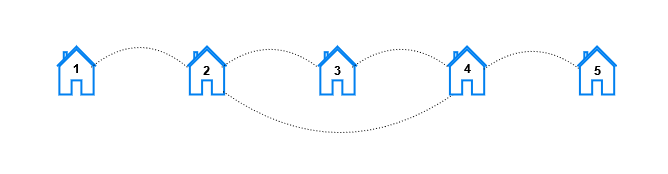
    Input: n = 5, x = 2, y = 4
    Output: [10,8,2,0,0]
    Explanation: For each distance k the pairs are:
    - For k == 1, the pairs are (1, 2), (2, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 4), (4, 3), (4, 5), and (5, 4).
    - For k == 2, the pairs are (1, 3), (3, 1), (1, 4), (4, 1), (2, 5), (5, 2), (3, 5), and (5, 3).
    - For k == 3, the pairs are (1, 5), and (5, 1).
    - For k == 4 and k == 5, there are no pairs.

Example 3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


![](https://assets.leetcode.com/uploads/2023/12/20/example5.png)

    
    
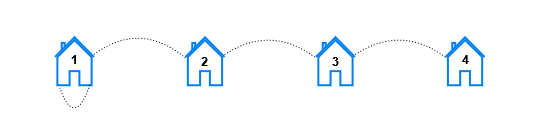
    Input: n = 4, x = 1, y = 1
    Output: [6,4,2,0]
    Explanation: For each distance k the pairs are:
    - For k == 1, the pairs are (1, 2), (2, 1), (2, 3), (3, 2), (3, 4), and (4, 3).
    - For k == 2, the pairs are (1, 3), (3, 1), (2, 4), and (4, 2).
    - For k == 3, the pairs are (1, 4), and (4, 1).
    - For k == 4, there are no pairs.

Constraints

  • 2 <= n <= 10^5
  • 1 <= x, y <= n

Solution

Method 1 – Shortest Path Enumeration (Math)

Intuition

For each pair of houses (i, j), the shortest path is either the direct path (|i-j|) or the path using the extra street (|i-x| + 1 + |j-y| or |i-y| + 1 + |j-x|). We count the number of pairs for each possible distance.

Approach

  1. For each pair (i, j) with i < j, compute the shortest distance:
    • Direct: |i-j|
    • Via extra street: min(|i-x| + 1 + |j-y|, |i-y| + 1 + |j-x|)
    • The minimum of the two is the shortest path.
  2. For each distance k, count the number of pairs with that distance.
  3. Since the graph is undirected, count both (i, j) and (j, i) (multiply by 2).
  4. Return the result array.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
public:
    vector<int> countOfPairs(int n, int x, int y) {
        vector<int> ans(n);
        for (int i = 1; i <= n; ++i) {
            for (int j = i+1; j <= n; ++j) {
                int d1 = abs(i-j);
                int d2 = min(abs(i-x)+1+abs(j-y), abs(i-y)+1+abs(j-x));
                int d = min(d1, d2);
                ans[d-1] += 2;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

type Solution struct{}
func (Solution) CountOfPairs(n, x, y int) []int {
    ans := make([]int, n)
    for i := 1; i <= n; i++ {
        for j := i+1; j <= n; j++ {
            d1 := abs(i-j)
            d2 := min(abs(i-x)+1+abs(j-y), abs(i-y)+1+abs(j-x))
            d := min(d1, d2)
            ans[d-1] += 2
        }
    }
    return ans
}
func abs(a int) int { if a < 0 { return -a }; return a }
func min(a, b int) int { if a < b { return a }; return b }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    public int[] countOfPairs(int n, int x, int y) {
        int[] ans = new int[n];
        for (int i = 1; i <= n; ++i) {
            for (int j = i+1; j <= n; ++j) {
                int d1 = Math.abs(i-j);
                int d2 = Math.min(Math.abs(i-x)+1+Math.abs(j-y), Math.abs(i-y)+1+Math.abs(j-x));
                int d = Math.min(d1, d2);
                ans[d-1] += 2;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    fun countOfPairs(n: Int, x: Int, y: Int): IntArray {
        val ans = IntArray(n)
        for (i in 1..n) {
            for (j in i+1..n) {
                val d1 = kotlin.math.abs(i-j)
                val d2 = minOf(kotlin.math.abs(i-x)+1+kotlin.math.abs(j-y), kotlin.math.abs(i-y)+1+kotlin.math.abs(j-x))
                val d = minOf(d1, d2)
                ans[d-1] += 2
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution:
    def countOfPairs(self, n: int, x: int, y: int) -> list[int]:
        ans = [0] * n
        for i in range(1, n+1):
            for j in range(i+1, n+1):
                d1 = abs(i-j)
                d2 = min(abs(i-x)+1+abs(j-y), abs(i-y)+1+abs(j-x))
                d = min(d1, d2)
                ans[d-1] += 2
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

impl Solution {
    pub fn count_of_pairs(n: i32, x: i32, y: i32) -> Vec<i32> {
        let n = n as usize;
        let mut ans = vec![0; n];
        for i in 1..=n {
            for j in i+1..=n {
                let d1 = (i as i32 - j as i32).abs();
                let d2 = ((i as i32 - x).abs() + 1 + (j as i32 - y).abs()).min((i as i32 - y).abs() + 1 + (j as i32 - x).abs());
                let d = d1.min(d2);
                ans[(d-1) as usize] += 2;
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    countOfPairs(n: number, x: number, y: number): number[] {
        const ans = Array(n).fill(0);
        for (let i = 1; i <= n; ++i) {
            for (let j = i+1; j <= n; ++j) {
                const d1 = Math.abs(i-j);
                const d2 = Math.min(Math.abs(i-x)+1+Math.abs(j-y), Math.abs(i-y)+1+Math.abs(j-x));
                const d = Math.min(d1, d2);
                ans[d-1] += 2;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), since we check all pairs of houses.
  • 🧺 Space complexity: O(n), for the result array.