Problem

Given a binary tree, write a program to count the number of Single Valued Subtrees. A Single Valued Subtree is one in which all the nodes have same value. Expected time complexity is O(n).

Example

Examples 1:

1
2
3
4
5

	  5
	 / \
	1   5
   / \   \
  5   5   5

1
2
3

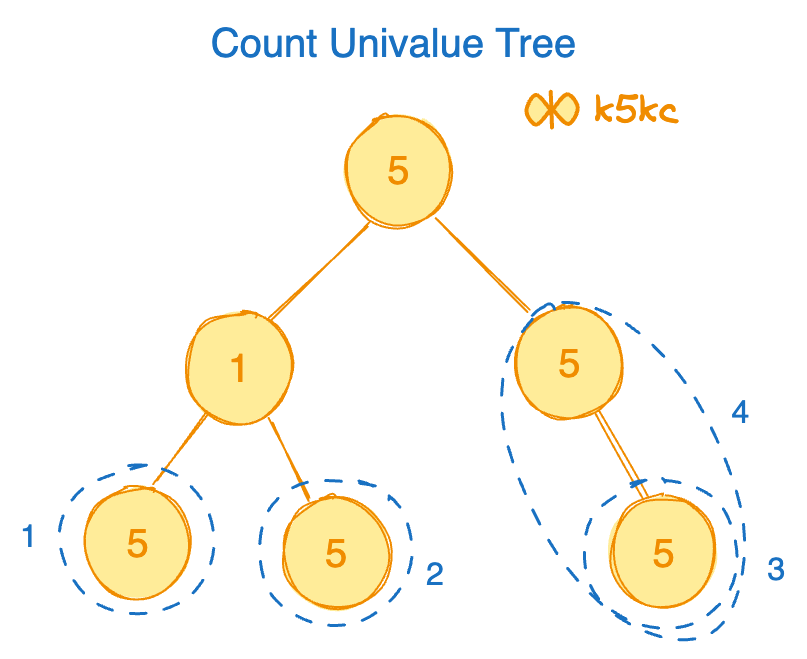
Input: root = [5,1,5,5,5,null,5]
Output: 4
Explanation: There are 4 subtrees with single values.(see below)

Examples 2:

1
2
3
4
5

	  5
	 / \
	4   5
   / \   \
  4   4   5

1
2

Input: root = [5,4,5,4,4,null,5]
Output: 5

Examples 3:

1
2
3
4
5

	  5
	 / \
	4   5
   / \   \
  4   4   5

1
2
3

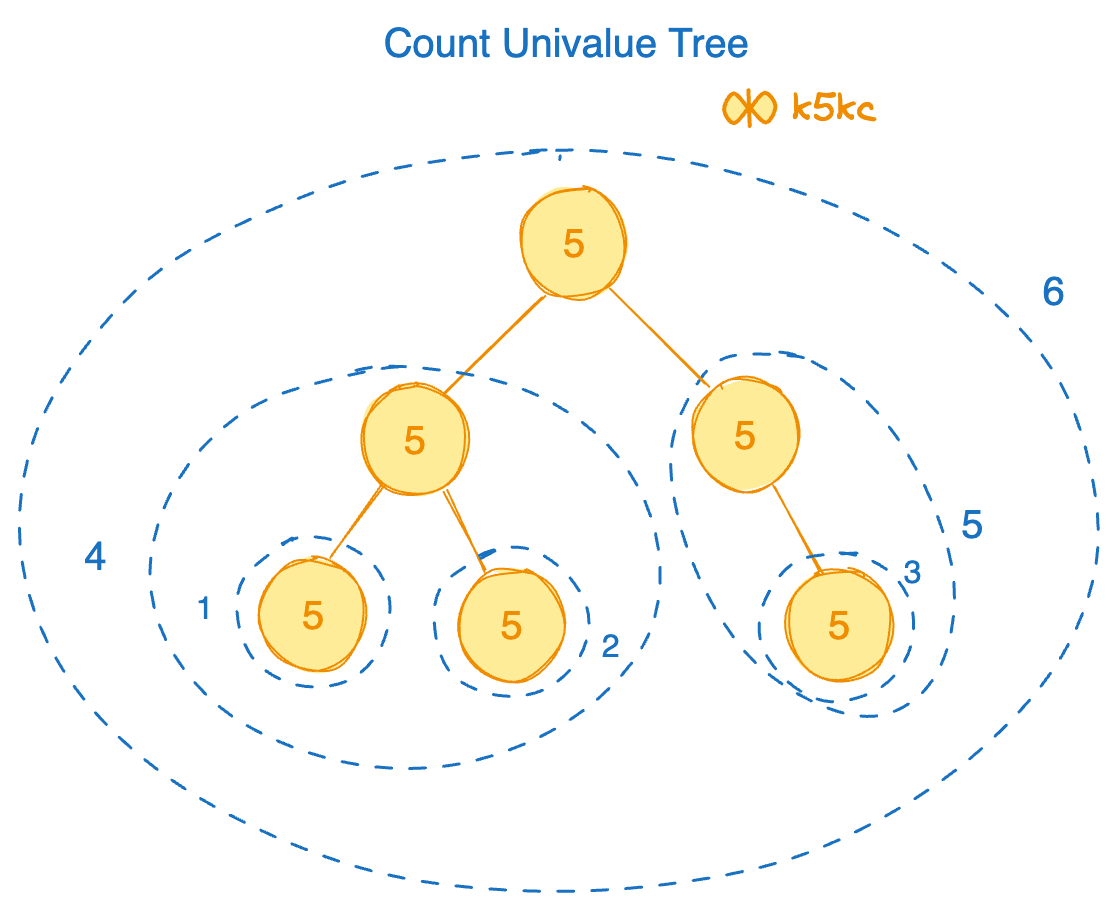
Input: root = [5,4,5,5,5,null,5]
Output: 6
Explanation: See image below

Solution

Method 1 - Brute Force

A Simple Solution is to traverse the tree. For every traversed node, check if all values under this node are same or not. If same, then increment count.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class Solution {

	public int countUnivalSubtrees(TreeNode root) {
		if (root == null) {
			return 0;
		}

		int ans = countUnivalTreeBad(root.left) + countUnivalTreeBad(root.right);

		if (isUnivalTree(root)) {
			ans += 1;
		}

		return ans;
	}

	private boolean isUnivalTree(TreeNode root) {
		if (root == null) {
			return true;
		}

		boolean left = isUnivalTree(root.left);
		boolean right = isUnivalTree(root.right);

		// If any of the subtrees is not singly, then this
		// cannot be singly.
		if (!left || !right) {
			return false;
		}

		// If left subtree is singly and non-empty, but data doesn't match
		if (root.left != null && root.val != root.left.val) {
			return false;
		}

		// Same for right subtree
		if (root.right != null && root.val != root.right.val) {
			return false;
		}

		return true;
	}
}

Complexity

  • ⏰ Time complexity: O(n^2). The time complexity on each step is O(n) for isUnival and we call it every time we traverse, so the time complexity is On(n^2).
  • 🧺 Space complexity: O(n)

Method 2 - Check Unival and Return counter in 1 call

We can calculate the count and check if the subtrees are univalue trees together. One way to do is to return array of object and return both together. Other ways is to use Wrapper class in java. We wrap the counter integer in Counter class.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

class Solution {

	private int ans;

	public int countUnivalSubtrees(TreeNode root) {
		dfs(root);
		return ans;
	}

	// This function increments counter ans by number of single
	// valued subtrees under root. It returns true if subtree
	// under root is Singly, else false.
	boolean dfs(TreeNode root) {
		// Return false to indicate NULL
		if (root == null) {
			return true;
		}

		// Recursively count in left and right subtrees also
		boolean left = dfs(root.left);
		boolean right = dfs(root.right);

		// If any of the subtrees is not singly, then this
		// cannot be singly.
		if (!left || !right) {
			return false;
		}

		// If left subtree is singly and non-empty, but data
		// doesn't match
		if (root.left != null && root.val != root.left.val) {
			return false;
		}

		// Same for right subtree
		if (root.right != null && root.val != root.right.val) {
			return false;
		}

		// If none of the above conditions is true, then
		// tree rooted under root is single valued, increment
		// count and return true.
		ans++;
		return true;
	}
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

def countUnivalSubtrees(root):
    count, _ = helper(root)
    return count;
def helper(root):
    if (root == null):
        return (0, true);

    leftCount, isLeftUnival = helper(root.left)
    rightCount, isRightUnival = helper(root.right)
 
    isUnival = True
    totalCount = leftCount + rightCount
    if not isLeftUnival or not isLeftUnival:
        isUnival = False

    if isUnival and root.left != null and root.val!=root.left.val:
        isUnival = False

    if isUnival and root.right != null and root.val!=root.right.val:
        isUnival = False

    if isUnival :
        totalCount += 1

    return totalCount

Complexity

  • ⏰ Time complexity: O(n), where n is number of nodes in given binary tree.
  • 🧺 Space complexity: O(n)