Count Unreachable Pairs of Nodes in an Undirected Graph
MediumUpdated: Aug 2, 2025
Practice on:
Count Unreachable Pairs of Nodes in an Undirected Graph Problem
Problem
You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.
Return the number of pairs of different nodes that are unreachable from each other.
Examples
Example 1:
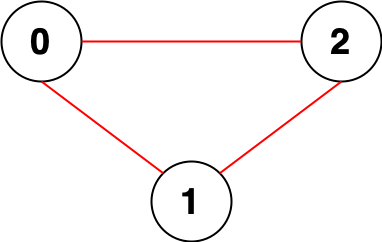
Input:
n = 3, edges = [[0,1],[0,2],[1,2]]
Output:
0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.
Example 2:
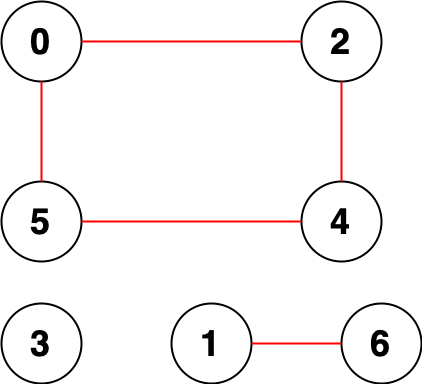
Input:
n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output:
14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.
Constraints:
1 <= n <= 1050 <= edges.length <= 2 * 105edges[i].length == 20 <= ai, bi < nai != bi- There are no repeated edges.
Solution
Method 1 – Connected Components (DFS/Union-Find) (1)
Intuition
The key idea is that nodes in the same connected component can reach each other, but nodes in different components cannot. So, for each component, count its size, and the number of unreachable pairs is the sum over all pairs of nodes in different components.
Approach
- Build the graph from the edge list.
- Use DFS or Union-Find to find all connected components and their sizes.
- For each component of size s, the number of unreachable pairs contributed is s * (total_nodes_remaining - s).
- Accumulate the answer as you process each component.
Code
C++
class Solution {
public:
long long countPairs(int n, vector<vector<int>>& edges) {
vector<vector<int>> g(n);
for (auto& e : edges) {
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vector<bool> vis(n);
function<int(int)> dfs = [&](int u) {
vis[u] = true;
int cnt = 1;
for (int v : g[u]) if (!vis[v]) cnt += dfs(v);
return cnt;
};
long long ans = 0, rem = n;
for (int i = 0; i < n; ++i) {
if (!vis[i]) {
int sz = dfs(i);
ans += (long long)sz * (rem - sz);
rem -= sz;
}
}
return ans;
}
};
Go
func countPairs(n int, edges [][]int) int64 {
g := make([][]int, n)
for _, e := range edges {
g[e[0]] = append(g[e[0]], e[1])
g[e[1]] = append(g[e[1]], e[0])
}
vis := make([]bool, n)
var dfs func(int) int
dfs = func(u int) int {
vis[u] = true
cnt := 1
for _, v := range g[u] {
if !vis[v] {
cnt += dfs(v)
}
}
return cnt
}
var ans int64
rem := n
for i := 0; i < n; i++ {
if !vis[i] {
sz := dfs(i)
ans += int64(sz) * int64(rem-sz)
rem -= sz
}
}
return ans
}
Java
class Solution {
public long countPairs(int n, int[][] edges) {
List<Integer>[] g = new List[n];
for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
for (int[] e : edges) {
g[e[0]].add(e[1]);
g[e[1]].add(e[0]);
}
boolean[] vis = new boolean[n];
long ans = 0, rem = n;
for (int i = 0; i < n; i++) {
if (!vis[i]) {
int sz = dfs(i, g, vis);
ans += (long)sz * (rem - sz);
rem -= sz;
}
}
return ans;
}
private int dfs(int u, List<Integer>[] g, boolean[] vis) {
vis[u] = true;
int cnt = 1;
for (int v : g[u]) if (!vis[v]) cnt += dfs(v, g, vis);
return cnt;
}
}
Kotlin
class Solution {
fun countPairs(n: Int, edges: Array<IntArray>): Long {
val g = Array(n) { mutableListOf<Int>() }
for (e in edges) {
g[e[0]].add(e[1])
g[e[1]].add(e[0])
}
val vis = BooleanArray(n)
var ans = 0L
var rem = n
fun dfs(u: Int): Int {
vis[u] = true
var cnt = 1
for (v in g[u]) if (!vis[v]) cnt += dfs(v)
return cnt
}
for (i in 0 until n) {
if (!vis[i]) {
val sz = dfs(i)
ans += sz.toLong() * (rem - sz)
rem -= sz
}
}
return ans
}
}
Python
class Solution:
def countPairs(self, n: int, edges: list[list[int]]) -> int:
g = [[] for _ in range(n)]
for u, v in edges:
g[u].append(v)
g[v].append(u)
vis = [False] * n
def dfs(u: int) -> int:
vis[u] = True
cnt = 1
for v in g[u]:
if not vis[v]:
cnt += dfs(v)
return cnt
ans = 0
rem = n
for i in range(n):
if not vis[i]:
sz = dfs(i)
ans += sz * (rem - sz)
rem -= sz
return ans
Rust
impl Solution {
pub fn count_pairs(n: i32, edges: Vec<Vec<i32>>) -> i64 {
let n = n as usize;
let mut g = vec![vec![]; n];
for e in &edges {
g[e[0] as usize].push(e[1] as usize);
g[e[1] as usize].push(e[0] as usize);
}
let mut vis = vec![false; n];
fn dfs(u: usize, g: &Vec<Vec<usize>>, vis: &mut Vec<bool>) -> i64 {
vis[u] = true;
let mut cnt = 1;
for &v in &g[u] {
if !vis[v] {
cnt += dfs(v, g, vis);
}
}
cnt
}
let mut ans = 0i64;
let mut rem = n as i64;
for i in 0..n {
if !vis[i] {
let sz = dfs(i, &g, &mut vis);
ans += sz * (rem - sz);
rem -= sz;
}
}
ans
}
}
TypeScript
class Solution {
countPairs(n: number, edges: number[][]): number {
const g: number[][] = Array.from({length: n}, () => []);
for (const [u, v] of edges) {
g[u].push(v);
g[v].push(u);
}
const vis = Array(n).fill(false);
let ans = 0, rem = n;
const dfs = (u: number): number => {
vis[u] = true;
let cnt = 1;
for (const v of g[u]) if (!vis[v]) cnt += dfs(v);
return cnt;
};
for (let i = 0; i < n; i++) {
if (!vis[i]) {
const sz = dfs(i);
ans += sz * (rem - sz);
rem -= sz;
}
}
return ans;
}
}
Complexity
- ⏰ Time complexity:
O(n + m), where n is the number of nodes and m is the number of edges; each node and edge is visited once. - 🧺 Space complexity:
O(n + m), for the adjacency list and visited array.