Count Visited Nodes in a Directed Graph
HardUpdated: Aug 2, 2025
Practice on:
Problem
There is a directed graph consisting of n nodes numbered from 0 to `n
- 1
andn` directed edges.
You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].
Consider the following process on the graph:
- You start from a node
xand keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.
Return an arrayanswer whereanswer[i]_is the number ofdifferent nodes that you will visit if you perform the process starting from node _i.
Examples
Example 1
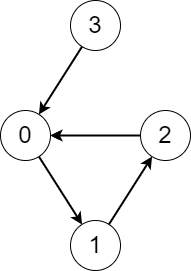
Input: edges = [1,2,0,0]
Output: [3,3,3,4]
Explanation: We perform the process starting from each node in the following way:
- Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
- Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
- Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
- Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.
Example 2
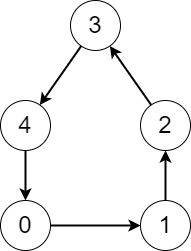
Input: edges = [1,2,3,4,0]
Output: [5,5,5,5,5]
Explanation: Starting from any node we can visit every node in the graph in the process.
Constraints
n == edges.length2 <= n <= 10^50 <= edges[i] <= n - 1edges[i] != i
Solution
Method 1 – Cycle Detection and Memoized DFS
Intuition
Each node leads to a path that either enters a cycle or ends at a node already visited. We can use DFS with memoization to count the number of unique nodes visited from each node, marking cycles and using a visited state to avoid recomputation.
Approach
- For each node, perform DFS to find the number of unique nodes visited starting from it.
- Use a state array: 0 = unvisited, 1 = visiting, 2 = visited.
- If a cycle is detected, mark all nodes in the cycle and set their answer to the cycle length.
- Use memoization to store the answer for each node.
- For nodes not in a cycle, the answer is 1 + answer of the next node.
Code
C++
class Solution {
public:
vector<int> countVisitedNodes(vector<int>& edges) {
int n = edges.size();
vector<int> ans(n, 0), state(n, 0);
function<int(int, vector<int>&)> dfs = [&](int u, vector<int>& path) -> int {
if (state[u] == 2) return ans[u];
if (state[u] == 1) {
int len = 1, v = edges[u];
while (v != u) { len++; v = edges[v]; }
v = u;
do { ans[v] = len; state[v] = 2; v = edges[v]; } while (v != u);
return len;
}
state[u] = 1;
path.push_back(u);
int res = 1 + dfs(edges[u], path);
if (state[u] != 2) {
ans[u] = res;
state[u] = 2;
}
path.pop_back();
return ans[u];
};
for (int i = 0; i < n; ++i) {
if (state[i] == 0) {
vector<int> path;
dfs(i, path);
}
}
return ans;
}
};
Go
func countVisitedNodes(edges []int) []int {
n := len(edges)
ans := make([]int, n)
state := make([]int, n)
var dfs func(int, []int) int
dfs = func(u int, path []int) int {
if state[u] == 2 {
return ans[u]
}
if state[u] == 1 {
len := 1
v := edges[u]
for v != u {
len++
v = edges[v]
}
v = u
for {
ans[v] = len
state[v] = 2
v = edges[v]
if v == u {
break
}
}
return len
}
state[u] = 1
path = append(path, u)
res := 1 + dfs(edges[u], path)
if state[u] != 2 {
ans[u] = res
state[u] = 2
}
return ans[u]
}
for i := 0; i < n; i++ {
if state[i] == 0 {
dfs(i, nil)
}
}
return ans
}
Java
class Solution {
public int[] countVisitedNodes(int[] edges) {
int n = edges.length;
int[] ans = new int[n], state = new int[n];
for (int i = 0; i < n; i++) {
if (state[i] == 0) dfs(i, edges, ans, state);
}
return ans;
}
private int dfs(int u, int[] edges, int[] ans, int[] state) {
if (state[u] == 2) return ans[u];
if (state[u] == 1) {
int len = 1, v = edges[u];
while (v != u) { len++; v = edges[v]; }
v = u;
do { ans[v] = len; state[v] = 2; v = edges[v]; } while (v != u);
return len;
}
state[u] = 1;
int res = 1 + dfs(edges[u], edges, ans, state);
if (state[u] != 2) {
ans[u] = res;
state[u] = 2;
}
return ans[u];
}
}
Kotlin
class Solution {
fun countVisitedNodes(edges: IntArray): IntArray {
val n = edges.size
val ans = IntArray(n)
val state = IntArray(n)
fun dfs(u: Int): Int {
if (state[u] == 2) return ans[u]
if (state[u] == 1) {
var len = 1
var v = edges[u]
while (v != u) { len++; v = edges[v] }
v = u
do {
ans[v] = len
state[v] = 2
v = edges[v]
} while (v != u)
return len
}
state[u] = 1
val res = 1 + dfs(edges[u])
if (state[u] != 2) {
ans[u] = res
state[u] = 2
}
return ans[u]
}
for (i in 0 until n) {
if (state[i] == 0) dfs(i)
}
return ans
}
}
Python
class Solution:
def countVisitedNodes(self, edges: list[int]) -> list[int]:
n = len(edges)
ans = [0] * n
state = [0] * n
def dfs(u: int) -> int:
if state[u] == 2:
return ans[u]
if state[u] == 1:
# found a cycle
v, l = edges[u], 1
while v != u:
l += 1
v = edges[v]
v = u
while True:
ans[v] = l
state[v] = 2
v = edges[v]
if v == u:
break
return l
state[u] = 1
res = 1 + dfs(edges[u])
if state[u] != 2:
ans[u] = res
state[u] = 2
return ans[u]
for i in range(n):
if state[i] == 0:
dfs(i)
return ans
Rust
impl Solution {
pub fn count_visited_nodes(edges: Vec<i32>) -> Vec<i32> {
let n = edges.len();
let mut ans = vec![0; n];
let mut state = vec![0; n];
fn dfs(u: usize, edges: &Vec<i32>, ans: &mut Vec<i32>, state: &mut Vec<i32>) -> i32 {
if state[u] == 2 { return ans[u]; }
if state[u] == 1 {
let mut v = edges[u] as usize;
let mut len = 1;
while v != u {
len += 1;
v = edges[v] as usize;
}
v = u;
loop {
ans[v] = len;
state[v] = 2;
v = edges[v] as usize;
if v == u { break; }
}
return len;
}
state[u] = 1;
let res = 1 + dfs(edges[u] as usize, edges, ans, state);
if state[u] != 2 {
ans[u] = res;
state[u] = 2;
}
ans[u]
}
for i in 0..n {
if state[i] == 0 {
dfs(i, &edges, &mut ans, &mut state);
}
}
ans
}
}
TypeScript
class Solution {
countVisitedNodes(edges: number[]): number[] {
const n = edges.length
const ans = new Array(n).fill(0)
const state = new Array(n).fill(0)
function dfs(u: number): number {
if (state[u] === 2) return ans[u]
if (state[u] === 1) {
let v = edges[u], len = 1
while (v !== u) { len++; v = edges[v] }
v = u
do {
ans[v] = len
state[v] = 2
v = edges[v]
} while (v !== u)
return len
}
state[u] = 1
const res = 1 + dfs(edges[u])
if (state[u] !== 2) {
ans[u] = res
state[u] = 2
}
return ans[u]
}
for (let i = 0; i < n; ++i) {
if (state[i] === 0) dfs(i)
}
return ans
}
}
Complexity
- ⏰ Time complexity:
O(n)since each node is visited at most twice (once in DFS, once in cycle marking). - 🧺 Space complexity:
O(n)for state and answer arrays.