Problem

There are n unique candies (labeled 1 through n) and k bags. You are asked to distribute all the candies into the bags such that every bag has at least one candy.

There can be multiple ways to distribute the candies. Two ways are considered different if the candies in one bag in the first way are not all in the same bag in the second way. The order of the bags and the order of the candies within each bag do not matter.

For example, (1), (2,3) and (2), (1,3) are considered different because candies 2 and 3 in the bag (2,3) in the first way are not in the same bag in the second way (they are split between the bags (_2_) and (1,_3_)). However, (1), (2,3) and (3,2), (1) are considered the same because the candies in each bag are all in the same bags in both ways.

Given two integers, n and k, return thenumber of different ways to distribute the candies. As the answer may be too large, return it modulo 109 + 7.

Examples

Example 1:

1
2
3
4
5
6
7

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1600-1699/1692.Count%20Ways%20to%20Distribute%20Candies/images/candies-1.png)
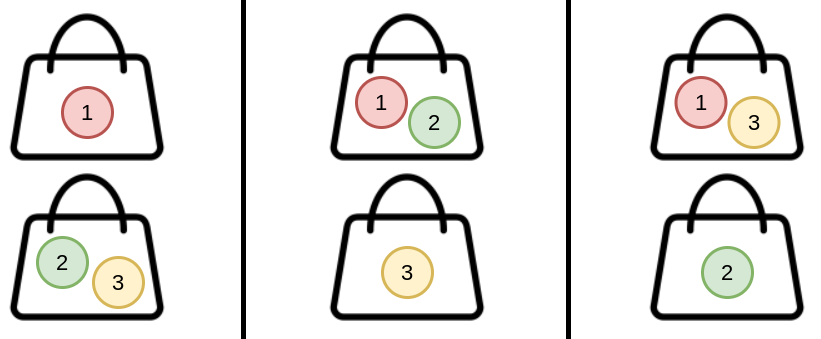
Input: n = 3, k = 2
Output: 3
Explanation: You can distribute 3 candies into 2 bags in 3 ways:
(1), (2,3)
(1,2), (3)
(1,3), (2)

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

Input: n = 4, k = 2
Output: 7
Explanation: You can distribute 4 candies into 2 bags in 7 ways:
(1), (2,3,4)
(1,2), (3,4)
(1,3), (2,4)
(1,4), (2,3)
(1,2,3), (4)
(1,2,4), (3)
(1,3,4), (2)

Example 3:

1
2
3

Input: n = 20, k = 5
Output: 206085257
Explanation: You can distribute 20 candies into 5 bags in 1881780996 ways. 1881780996 modulo 109 + 7 = 206085257.

Constraints:

  • 1 <= k <= n <= 1000

Solution

Method 1 – Dynamic Programming with Stirling Numbers of the Second Kind

Intuition

The key idea is to count the number of ways to partition n unique candies into k non-empty bags, where the order of bags doesn’t matter, but the distribution of candies does. This is exactly the Stirling numbers of the second kind, S(n, k).

Approach

  1. Let S(n, k) be the number of ways to partition n candies into k non-empty bags.
  2. The recurrence is:
    • S(n, k) = k * S(n-1, k) + S(n-1, k-1)
    • Base cases:
      • S(0, 0) = 1
      • S(n, 0) = 0 for n > 0
      • S(0, k) = 0 for k > 0
  3. Use dynamic programming to fill a 2D table dp[n+1][k+1] with modulo 1e9+7.
  4. Return dp[n][k].

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int countWays(int n, int k) {
        const int MOD = 1e9 + 7;
        vector<vector<int>> dp(n+1, vector<int>(k+1, 0));
        dp[0][0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= k; ++j) {
                dp[i][j] = (1LL * j * dp[i-1][j] % MOD + dp[i-1][j-1]) % MOD;
            }
        }
        return dp[n][k];
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

func countWays(n int, k int) int {
    const mod = 1e9 + 7
    dp := make([][]int, n+1)
    for i := range dp {
        dp[i] = make([]int, k+1)
    }
    dp[0][0] = 1
    for i := 1; i <= n; i++ {
        for j := 1; j <= k; j++ {
            dp[i][j] = (j*dp[i-1][j]%mod + dp[i-1][j-1]) % mod
        }
    }
    return dp[n][k]
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    public int countWays(int n, int k) {
        int MOD = 1000000007;
        int[][] dp = new int[n+1][k+1];
        dp[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= k; j++) {
                dp[i][j] = (int)(((long)j * dp[i-1][j] % MOD + dp[i-1][j-1]) % MOD);
            }
        }
        return dp[n][k];
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    fun countWays(n: Int, k: Int): Int {
        val MOD = 1_000_000_007
        val dp = Array(n+1) { IntArray(k+1) }
        dp[0][0] = 1
        for (i in 1..n) {
            for (j in 1..k) {
                dp[i][j] = ((j.toLong() * dp[i-1][j] % MOD + dp[i-1][j-1]) % MOD).toInt()
            }
        }
        return dp[n][k]
    }
}
1
2
3
4
5
6
7
8
9

class Solution:
    def countWays(self, n: int, k: int) -> int:
        MOD = 10**9 + 7
        dp: list[list[int]] = [[0] * (k+1) for _ in range(n+1)]
        dp[0][0] = 1
        for i in range(1, n+1):
            for j in range(1, k+1):
                dp[i][j] = (j * dp[i-1][j] + dp[i-1][j-1]) % MOD
        return dp[n][k]
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

impl Solution {
    pub fn count_ways(n: i32, k: i32) -> i32 {
        let n = n as usize;
        let k = k as usize;
        let m = 1_000_000_007;
        let mut dp = vec![vec![0; k+1]; n+1];
        dp[0][0] = 1;
        for i in 1..=n {
            for j in 1..=k {
                dp[i][j] = ((j as i64 * dp[i-1][j] as i64 % m + dp[i-1][j] as i64) % m) as i32;
            }
        }
        dp[n][k]
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    countWays(n: number, k: number): number {
        const MOD = 1e9 + 7;
        const dp: number[][] = Array.from({length: n+1}, () => Array(k+1).fill(0));
        dp[0][0] = 1;
        for (let i = 1; i <= n; i++) {
            for (let j = 1; j <= k; j++) {
                dp[i][j] = (j * dp[i-1][j] % MOD + dp[i-1][j-1]) % MOD;
            }
        }
        return dp[n][k];
    }
}

Complexity

  • ⏰ Time complexity: O(n*k), because we fill an n x k table, each cell in constant time.
  • 🧺 Space complexity: O(n*k), for the DP table storing all subproblem results.