Count Ways to Tile a 3xN Board using 1x3 and 3x1 tiles

Problem

Given a 3 × N rectangle, determine the number of ways to tile it using tiles of size 1 × 3 (horizontal tromino) and 3 × 1 (vertical tromino). You may place tiles only with integer grid alignment; tiles cannot overlap or go outside the board.

Input: integer N (1 ≤ N ≤ 15)

Output: number of distinct tilings of a 3 × N board using the given tiles.

Examples

Example 1

Input: N = 4
Output: 3

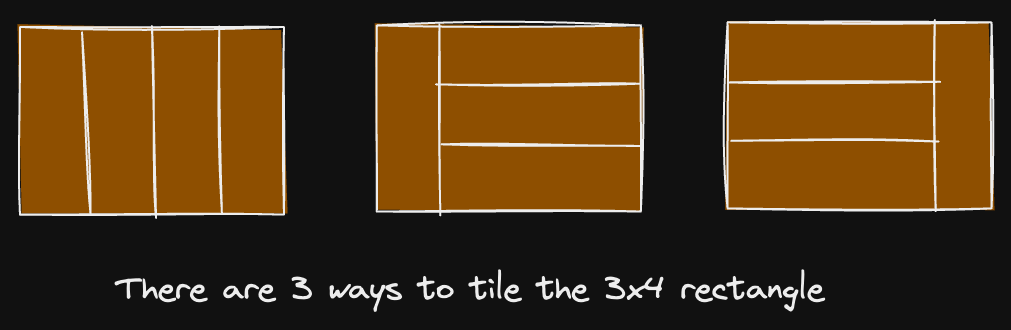
Solution

This is a standard tiling/counting DP. Let f(n) be the number of ways to tile a 3 × n board. There are two mutually exclusive choices for filling the leftmost part of the board:

• Place a single vertical 3×1 tile in column 1 — this reduces the problem to 3 × (n-1) and contributes f(n-1) ways.
• Place three horizontal 1×3 tiles (one in each row) covering columns 1..3 — this reduces to 3 × (n-3) and contributes f(n-3) ways.

Therefore the recurrence is:

f(n) = f(n-1) + f(n-3)

With base cases f(0) = 1 (empty board), f(1) = 1 (one vertical column), and f(2) = 1 (two vertical columns). This recurrence matches the sample: f(4) = f(3) + f(1) = 2 + 1 = 3.

We present a simple bottom-up DP implementation and path-free counting (only counts ways).

Method 1 — Bottom-up DP (iterative)

Intuition

Fill the board from left to right. At each step either consume one column with a vertical tile or consume three columns with three horizontals. This yields a linear recurrence depending only on smaller n values.

Approach

1. Handle small n directly: return 1 for n = 0,1,2 as base cases.
2. Allocate array dp[0..n] and set dp[0]=dp[1]=dp[2]=1.
3. For i from 3 to n compute dp[i] = dp[i-1] + dp[i-3].
4. Return dp[n].

Edge cases: N may be 0 (empty board) — treat f(0)=1.

Code

C++

class Solution {
 public:
  int ways(int n) {
    if (n <= 2) return 1;
    vector<int> dp(n+1);
    dp[0] = dp[1] = dp[2] = 1;
    for (int i = 3; i <= n; ++i) dp[i] = dp[i-1] + dp[i-3];
    return dp[n];
  }
};

Go

package main

func ways(n int) int {
    if n <= 2 { return 1 }
    dp := make([]int, n+1)
    dp[0], dp[1], dp[2] = 1, 1, 1
    for i := 3; i <= n; i++ { dp[i] = dp[i-1] + dp[i-3] }
    return dp[n]
}

Java

class Solution {
  public int ways(int n) {
    if (n <= 2) return 1;
    long[] dp = new long[n+1];
    dp[0] = dp[1] = dp[2] = 1;
    for (int i = 3; i <= n; ++i) dp[i] = dp[i-1] + dp[i-3];
    return dp[n];
  }
}

Python

from typing import List

class Solution:
    def ways(self, n: int) -> int:
        if n <= 2:
            return 1
        dp: List[int] = [0] * (n + 1)
        dp[0] = dp[1] = dp[2] = 1
        for i in range(3, n+1):
            dp[i] = dp[i-1] + dp[i-3]
        return dp[n]

Complexity

• ⏰ Time complexity: O(n) — compute values for dp[3..n] with constant work each step.
• 🧺 Space complexity: O(n) for the dp array. This can be reduced to O(1) by keeping only the last three values.