Problem

There is an undirected tree with n nodes labeled from 0 to n - 1.

You are given a 0-indexed integer array nums of length n where nums[i] represents the value of the ith node. You are also given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are allowed to delete some edges, splitting the tree into multiple connected components. Let the value of a component be the sum of all nums[i] for which node i is in the component.

Return themaximum number of edges you can delete, such that every connected component in the tree has the same value.

Examples

Example 1

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2022/08/26/diagramdrawio.png)

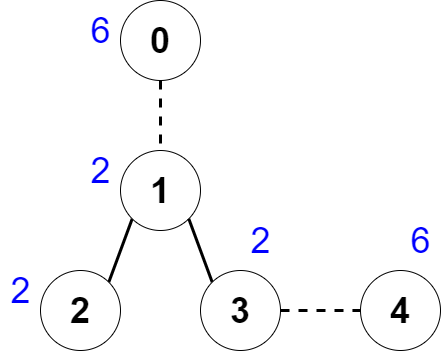
Input: nums = [6,2,2,2,6], edges = [[0,1],[1,2],[1,3],[3,4]] 
Output: 2 
Explanation: The above figure shows how we can delete the edges [0,1] and [3,4]. The created components are nodes [0], [1,2,3] and [4]. The sum of the values in each component equals 6. It can be proven that no better deletion exists, so the answer is 2.

Example 2

1
2
3

Input: nums = [2], edges = []
Output: 0
Explanation: There are no edges to be deleted.

Constraints

  • 1 <= n <= 2 * 10^4
  • nums.length == n
  • 1 <= nums[i] <= 50
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= edges[i][0], edges[i][1] <= n - 1
  • edges represents a valid tree.

Solution

Method 1 – DFS with Divisor Enumeration

Intuition

The key idea is to split the tree into components with equal sum by removing edges. The sum of each component must be a divisor of the total sum. For each divisor, we use DFS to check if we can partition the tree into components of that sum by counting how many subtrees sum to the target.

Approach

  1. Compute the total sum of all node values.
  2. Enumerate all divisors of the total sum (possible component sums).
  3. For each divisor (target sum):
    • Use DFS to count how many subtrees sum to the target. Each time a subtree sums to the target, treat it as a component and reset its sum to 0.
    • If the number of components equals total_sum // target, update the answer.
  4. Return the maximum number of edges that can be removed, which is the number of components minus 1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

class Solution {
public:
    int componentValue(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size();
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        int total = accumulate(nums.begin(), nums.end(), 0);
        int ans = 0;
        for (int k = 1; k * k <= total; ++k) {
            if (total % k == 0) {
                for (int target : {k, total / k}) {
                    if (target < total) {
                        int cnt = 0;
                        function<int(int, int)> dfs = [&](int u, int p) {
                            int sum = nums[u];
                            for (int v : g[u]) if (v != p) sum += dfs(v, u);
                            if (sum == target) { ++cnt; return 0; }
                            return sum;
                        };
                        dfs(0, -1);
                        if (cnt == total / target) ans = max(ans, cnt - 1);
                    }
                }
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

func componentValue(nums []int, edges [][]int) int {
    n := len(nums)
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    total := 0
    for _, v := range nums {
        total += v
    }
    ans := 0
    for k := 1; k*k <= total; k++ {
        if total%k == 0 {
            for _, target := range []int{k, total / k} {
                if target < total {
                    cnt := 0
                    var dfs func(u, p int) int
                    dfs = func(u, p int) int {
                        sum := nums[u]
                        for _, v := range g[u] {
                            if v != p {
                                sum += dfs(v, u)
                            }
                        }
                        if sum == target {
                            cnt++
                            return 0
                        }
                        return sum
                    }
                    dfs(0, -1)
                    if cnt == total/target && ans < cnt-1 {
                        ans = cnt - 1
                    }
                }
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

class Solution {
    public int componentValue(int[] nums, int[][] edges) {
        int n = nums.length;
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        for (int[] e : edges) {
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        int total = 0;
        for (int v : nums) total += v;
        int ans = 0;
        for (int k = 1; k * k <= total; k++) {
            if (total % k == 0) {
                for (int target : new int[]{k, total / k}) {
                    if (target < total) {
                        int[] cnt = new int[1];
                        dfs(0, -1, g, nums, target, cnt);
                        if (cnt[0] == total / target && ans < cnt[0] - 1) ans = cnt[0] - 1;
                    }
                }
            }
        }
        return ans;
    }
    private int dfs(int u, int p, List<Integer>[] g, int[] nums, int target, int[] cnt) {
        int sum = nums[u];
        for (int v : g[u]) if (v != p) sum += dfs(v, u, g, nums, target, cnt);
        if (sum == target) {
            cnt[0]++;
            return 0;
        }
        return sum;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Solution {
    fun componentValue(nums: IntArray, edges: Array<IntArray>): Int {
        val n = nums.size
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val total = nums.sum()
        var ans = 0
        for (k in 1..total) {
            if (k * k > total) break
            if (total % k == 0) {
                for (target in listOf(k, total / k)) {
                    if (target < total) {
                        var cnt = 0
                        fun dfs(u: Int, p: Int): Int {
                            var sum = nums[u]
                            for (v in g[u]) if (v != p) sum += dfs(v, u)
                            if (sum == target) {
                                cnt++
                                return 0
                            }
                            return sum
                        }
                        dfs(0, -1)
                        if (cnt == total / target && ans < cnt - 1) ans = cnt - 1
                    }
                }
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution:
    def componentValue(self, nums: list[int], edges: list[list[int]]) -> int:
        from math import isqrt
        n = len(nums)
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        total = sum(nums)
        ans = 0
        for k in range(1, isqrt(total) + 1):
            if total % k == 0:
                for target in [k, total // k]:
                    if target < total:
                        cnt = 0
                        def dfs(u, p):
                            nonlocal cnt
                            s = nums[u]
                            for v in g[u]:
                                if v != p:
                                    s += dfs(v, u)
                            if s == target:
                                cnt += 1
                                return 0
                            return s
                        dfs(0, -1)
                        if cnt == total // target and ans < cnt - 1:
                            ans = cnt - 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

impl Solution {
    pub fn component_value(nums: Vec<i32>, edges: Vec<Vec<i32>>) -> i32 {
        let n = nums.len();
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let total: i32 = nums.iter().sum();
        let mut ans = 0;
        let mut k = 1;
        while k * k <= total {
            if total % k == 0 {
                for &target in &[k, total / k] {
                    if target < total {
                        let mut cnt = 0;
                        fn dfs(u: usize, p: i32, g: &Vec<Vec<usize>>, nums: &Vec<i32>, target: i32, cnt: &mut i32) -> i32 {
                            let mut sum = nums[u];
                            for &v in &g[u] {
                                if v as i32 != p {
                                    sum += dfs(v, u as i32, g, nums, target, cnt);
                                }
                            }
                            if sum == target {
                                *cnt += 1;
                                return 0;
                            }
                            sum
                        }
                        dfs(0, -1, &g, &nums, target, &mut cnt);
                        if cnt == total / target && ans < cnt - 1 {
                            ans = cnt - 1;
                        }
                    }
                }
            }
            k += 1;
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    componentValue(nums: number[], edges: number[][]): number {
        const n = nums.length;
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [a, b] of edges) {
            g[a].push(b);
            g[b].push(a);
        }
        const total = nums.reduce((a, b) => a + b, 0);
        let ans = 0;
        for (let k = 1; k * k <= total; k++) {
            if (total % k === 0) {
                for (const target of [k, total / k]) {
                    if (target < total) {
                        let cnt = 0;
                        function dfs(u: number, p: number): number {
                            let sum = nums[u];
                            for (const v of g[u]) if (v !== p) sum += dfs(v, u);
                            if (sum === target) {
                                cnt++;
                                return 0;
                            }
                            return sum;
                        }
                        dfs(0, -1);
                        if (cnt === total / target && ans < cnt - 1) ans = cnt - 1;
                    }
                }
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n * sqrt(S)), where n is the number of nodes and S is the total sum of nums, due to divisor enumeration and DFS for each divisor.
  • 🧺 Space complexity: O(n), for the adjacency list and recursion stack.