Problem

You are asked to cut off all the trees in a forest for a golf event. The forest is represented as an m x n matrix. In this matrix:

  • 0 means the cell cannot be walked through.
  • 1 represents an empty cell that can be walked through.
  • A number greater than 1 represents a tree in a cell that can be walked through, and this number is the tree’s height.

In one step, you can walk in any of the four directions: north, east, south, and west. If you are standing in a cell with a tree, you can choose whether to cut it off.

You must cut off the trees in order from shortest to tallest. When you cut off a tree, the value at its cell becomes 1 (an empty cell).

Starting from the point (0, 0), return the minimum steps you need to walk to cut off all the trees. If you cannot cut off all the trees, return -1.

Note: The input is generated such that no two trees have the same height, and there is at least one tree needs to be cut off.

Examples

Example 1

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2020/11/26/trees1.jpg)

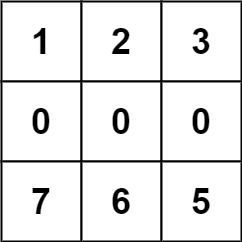
Input: forest = [[1,2,3],[0,0,4],[7,6,5]]
Output: 6
Explanation: Following the path above allows you to cut off the trees from shortest to tallest in 6 steps.

Example 2

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2020/11/26/trees2.jpg)

Input: forest = [[1,2,3],[0,0,0],[7,6,5]]
Output: -1
Explanation: The trees in the bottom row cannot be accessed as the middle row is blocked.

Example 3

1
2
3
4

Input: forest = [[2,3,4],[0,0,5],[8,7,6]]
Output: 6
Explanation: You can follow the same path as Example 1 to cut off all the trees.
Note that you can cut off the first tree at (0, 0) before making any steps.

Constraints

  • m == forest.length
  • n == forest[i].length
  • 1 <= m, n <= 50
  • 0 <= forest[i][j] <= 10^9
  • Heights of all trees are distinct.

Solution

Method 1 – BFS for Shortest Path Between Trees

Intuition

The key idea is to cut the trees in order of increasing height, always moving from the current position to the next tree using the shortest path. Since the grid is small, we can use BFS to find the shortest path between any two points, treating obstacles as impassable.

Approach

  1. Collect all trees (cells with value > 1) and their positions, then sort them by height.
  2. Start from (0, 0). For each tree in order:
    • Use BFS to find the minimum steps from the current position to the tree’s position.
    • If a tree is unreachable, return -1.
    • Move to the tree’s position and set its cell to 1 (cut the tree).
  3. Sum the steps for all trees and return the total.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
public:
    int cutOffTree(vector<vector<int>>& forest) {
        int m = forest.size(), n = forest[0].size();
        vector<tuple<int, int, int>> trees;
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (forest[i][j] > 1)
                    trees.emplace_back(forest[i][j], i, j);
        sort(trees.begin(), trees.end());
        auto bfs = [&](int sx, int sy, int tx, int ty) {
            if (sx == tx && sy == ty) return 0;
            vector<vector<int>> vis(m, vector<int>(n, 0));
            queue<pair<int, int>> q;
            q.push({sx, sy});
            vis[sx][sy] = 1;
            int d = 0;
            int dirs[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
            while (!q.empty()) {
                int sz = q.size();
                ++d;
                while (sz--) {
                    auto [x, y] = q.front(); q.pop();
                    for (auto& dir : dirs) {
                        int nx = x + dir[0], ny = y + dir[1];
                        if (nx >= 0 && nx < m && ny >= 0 && ny < n && !vis[nx][ny] && forest[nx][ny] != 0) {
                            if (nx == tx && ny == ty) return d;
                            vis[nx][ny] = 1;
                            q.push({nx, ny});
                        }
                    }
                }
            }
            return -1;
        };
        int ans = 0, cx = 0, cy = 0;
        for (auto& [h, x, y] : trees) {
            int d = bfs(cx, cy, x, y);
            if (d == -1) return -1;
            ans += d;
            cx = x; cy = y;
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

func cutOffTree(forest [][]int) int {
    m, n := len(forest), len(forest[0])
    type tree struct{ h, x, y int }
    var trees []tree
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if forest[i][j] > 1 {
                trees = append(trees, tree{forest[i][j], i, j})
            }
        }
    }
    sort.Slice(trees, func(i, j int) bool { return trees[i].h < trees[j].h })
    dirs := [][2]int{{0,1},{1,0},{0,-1},{-1,0}}
    bfs := func(sx, sy, tx, ty int) int {
        if sx == tx && sy == ty {
            return 0
        }
        vis := make([][]bool, m)
        for i := range vis {
            vis[i] = make([]bool, n)
        }
        q := [][2]int{{sx, sy}}
        vis[sx][sy] = true
        d := 0
        for len(q) > 0 {
            d++
            sz := len(q)
            for i := 0; i < sz; i++ {
                x, y := q[0][0], q[0][1]
                q = q[1:]
                for _, dir := range dirs {
                    nx, ny := x+dir[0], y+dir[1]
                    if nx >= 0 && nx < m && ny >= 0 && ny < n && !vis[nx][ny] && forest[nx][ny] != 0 {
                        if nx == tx && ny == ty {
                            return d
                        }
                        vis[nx][ny] = true
                        q = append(q, [2]int{nx, ny})
                    }
                }
            }
        }
        return -1
    }
    ans, cx, cy := 0, 0, 0
    for _, t := range trees {
        d := bfs(cx, cy, t.x, t.y)
        if d == -1 {
            return -1
        }
        ans += d
        cx, cy = t.x, t.y
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution {
    public int cutOffTree(List<List<Integer>> forest) {
        int m = forest.size(), n = forest.get(0).size();
        List<int[]> trees = new ArrayList<>();
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (forest.get(i).get(j) > 1)
                    trees.add(new int[]{forest.get(i).get(j), i, j});
        trees.sort(Comparator.comparingInt(a -> a[0]));
        int ans = 0, cx = 0, cy = 0;
        for (int[] t : trees) {
            int d = bfs(forest, cx, cy, t[1], t[2]);
            if (d == -1) return -1;
            ans += d;
            cx = t[1]; cy = t[2];
        }
        return ans;
    }
    private int bfs(List<List<Integer>> forest, int sx, int sy, int tx, int ty) {
        if (sx == tx && sy == ty) return 0;
        int m = forest.size(), n = forest.get(0).size();
        boolean[][] vis = new boolean[m][n];
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[]{sx, sy});
        vis[sx][sy] = true;
        int d = 0;
        int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
        while (!q.isEmpty()) {
            int sz = q.size();
            d++;
            for (int i = 0; i < sz; i++) {
                int[] cur = q.poll();
                for (int[] dir : dirs) {
                    int nx = cur[0] + dir[0], ny = cur[1] + dir[1];
                    if (nx >= 0 && nx < m && ny >= 0 && ny < n && !vis[nx][ny] && forest.get(nx).get(ny) != 0) {
                        if (nx == tx && ny == ty) return d;
                        vis[nx][ny] = true;
                        q.offer(new int[]{nx, ny});
                    }
                }
            }
        }
        return -1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

class Solution {
    fun cutOffTree(forest: List<List<Int>>): Int {
        val m = forest.size
        val n = forest[0].size
        val trees = mutableListOf<Triple<Int, Int, Int>>()
        for (i in 0 until m)
            for (j in 0 until n)
                if (forest[i][j] > 1)
                    trees.add(Triple(forest[i][j], i, j))
        trees.sortBy { it.first }
        var ans = 0
        var cx = 0
        var cy = 0
        for ((_, x, y) in trees) {
            val d = bfs(forest, cx, cy, x, y)
            if (d == -1) return -1
            ans += d
            cx = x; cy = y
        }
        return ans
    }
    private fun bfs(forest: List<List<Int>>, sx: Int, sy: Int, tx: Int, ty: Int): Int {
        if (sx == tx && sy == ty) return 0
        val m = forest.size
        val n = forest[0].size
        val vis = Array(m) { BooleanArray(n) }
        val q = ArrayDeque<Pair<Int, Int>>()
        q.add(Pair(sx, sy))
        vis[sx][sy] = true
        var d = 0
        val dirs = arrayOf(0 to 1, 1 to 0, 0 to -1, -1 to 0)
        while (q.isNotEmpty()) {
            val sz = q.size
            d++
            repeat(sz) {
                val (x, y) = q.removeFirst()
                for ((dx, dy) in dirs) {
                    val nx = x + dx
                    val ny = y + dy
                    if (nx in 0 until m && ny in 0 until n && !vis[nx][ny] && forest[nx][ny] != 0) {
                        if (nx == tx && ny == ty) return d
                        vis[nx][ny] = true
                        q.add(Pair(nx, ny))
                    }
                }
            }
        }
        return -1
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution:
    def cutOffTree(self, forest: list[list[int]]) -> int:
        from collections import deque
        m, n = len(forest), len(forest[0])
        trees = sorted((h, i, j) for i, row in enumerate(forest) for j, h in enumerate(row) if h > 1)
        def bfs(sx, sy, tx, ty):
            if sx == tx and sy == ty:
                return 0
            vis = [[False]*n for _ in range(m)]
            q = deque([(sx, sy)])
            vis[sx][sy] = True
            d = 0
            dirs = [(0,1),(1,0),(0,-1),(-1,0)]
            while q:
                d += 1
                for _ in range(len(q)):
                    x, y = q.popleft()
                    for dx, dy in dirs:
                        nx, ny = x+dx, y+dy
                        if 0 <= nx < m and 0 <= ny < n and not vis[nx][ny] and forest[nx][ny] != 0:
                            if nx == tx and ny == ty:
                                return d
                            vis[nx][ny] = True
                            q.append((nx, ny))
            return -1
        ans, cx, cy = 0, 0, 0
        for _, x, y in trees:
            d = bfs(cx, cy, x, y)
            if d == -1:
                return -1
            ans += d
            cx, cy = x, y
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

impl Solution {
    pub fn cut_off_tree(forest: Vec<Vec<i32>>) -> i32 {
        let m = forest.len();
        let n = forest[0].len();
        let mut trees = vec![];
        for i in 0..m {
            for j in 0..n {
                if forest[i][j] > 1 {
                    trees.push((forest[i][j], i, j));
                }
            }
        }
        trees.sort();
        let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
        let bfs = |sx: usize, sy: usize, tx: usize, ty: usize, forest: &Vec<Vec<i32>>| -> i32 {
            if sx == tx && sy == ty { return 0; }
            let mut vis = vec![vec![false; n]; m];
            let mut q = std::collections::VecDeque::new();
            q.push_back((sx, sy));
            vis[sx][sy] = true;
            let mut d = 0;
            while !q.is_empty() {
                d += 1;
                for _ in 0..q.len() {
                    let (x, y) = q.pop_front().unwrap();
                    for (dx, dy) in dirs.iter() {
                        let nx = x as i32 + dx;
                        let ny = y as i32 + dy;
                        if nx >= 0 && nx < m as i32 && ny >= 0 && ny < n as i32 {
                            let nx = nx as usize;
                            let ny = ny as usize;
                            if !vis[nx][ny] && forest[nx][ny] != 0 {
                                if nx == tx && ny == ty { return d; }
                                vis[nx][ny] = true;
                                q.push_back((nx, ny));
                            }
                        }
                    }
                }
            }
            -1
        };
        let mut ans = 0;
        let (mut cx, mut cy) = (0, 0);
        for &(_, x, y) in &trees {
            let d = bfs(cx, cy, x, y, &forest);
            if d == -1 { return -1; }
            ans += d;
            cx = x; cy = y;
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class Solution {
    cutOffTree(forest: number[][]): number {
        const m = forest.length, n = forest[0].length;
        const trees: [number, number, number][] = [];
        for (let i = 0; i < m; i++)
            for (let j = 0; j < n; j++)
                if (forest[i][j] > 1)
                    trees.push([forest[i][j], i, j]);
        trees.sort((a, b) => a[0] - b[0]);
        const dirs = [[0,1],[1,0],[0,-1],[-1,0]];
        function bfs(sx: number, sy: number, tx: number, ty: number): number {
            if (sx === tx && sy === ty) return 0;
            const vis = Array.from({length: m}, () => Array(n).fill(false));
            const q: [number, number][] = [[sx, sy]];
            vis[sx][sy] = true;
            let d = 0;
            while (q.length) {
                d++;
                for (let sz = q.length; sz > 0; sz--) {
                    const [x, y] = q.shift()!;
                    for (const [dx, dy] of dirs) {
                        const nx = x + dx, ny = y + dy;
                        if (nx >= 0 && nx < m && ny >= 0 && ny < n && !vis[nx][ny] && forest[nx][ny] !== 0) {
                            if (nx === tx && ny === ty) return d;
                            vis[nx][ny] = true;
                            q.push([nx, ny]);
                        }
                    }
                }
            }
            return -1;
        }
        let ans = 0, cx = 0, cy = 0;
        for (const [, x, y] of trees) {
            const d = bfs(cx, cy, x, y);
            if (d === -1) return -1;
            ans += d;
            cx = x; cy = y;
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(T * m * n), where T is the number of trees, and each BFS is O(mn).
  • 🧺 Space complexity: O(mn), for the visited array in BFS.