Problem

You are given an integer n. There is a complete binary tree with 2n -1 nodes. The root of that tree is the node with the value 1, and every node with a value val in the range [1, 2n - 1 - 1] has two children where:

  • The left node has the value 2 * val, and
  • The right node has the value 2 * val + 1.

You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, solve the following problem:

  1. Add an edge between the nodes with values ai and bi.
  2. Find the length of the cycle in the graph.
  3. Remove the added edge between nodes with values ai and bi.

Note that:

  • A cycle is a path that starts and ends at the same node, and each edge in the path is visited only once.
  • The length of a cycle is the number of edges visited in the cycle.
  • There could be multiple edges between two nodes in the tree after adding the edge of the query.

Return an arrayanswer of lengthm where answer[i] is the answer to the ith query.

Examples

Example 1

1
2
3
4
5
6
7
8
9


![](https://assets.leetcode.com/uploads/2022/10/25/bexample1.png)

Input: n = 3, queries = [[5,3],[4,7],[2,3]]
Output: [4,5,3]
Explanation: The diagrams above show the tree of 23 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 3 and 5, the graph contains a cycle of nodes [5,2,1,3]. Thus answer to the first query is 4. We delete the added edge and process the next query.
- After adding the edge between nodes 4 and 7, the graph contains a cycle of nodes [4,2,1,3,7]. Thus answer to the second query is 5. We delete the added edge and process the next query.
- After adding the edge between nodes 2 and 3, the graph contains a cycle of nodes [2,1,3]. Thus answer to the third query is 3. We delete the added edge.

Example 2

1
2
3
4
5
6
7


![](https://assets.leetcode.com/uploads/2022/10/25/aexample2.png)

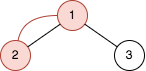
Input: n = 2, queries = [[1,2]]
Output: [2]
Explanation: The diagram above shows the tree of 22 - 1 nodes. Nodes colored in red describe the nodes in the cycle after adding the edge.
- After adding the edge between nodes 1 and 2, the graph contains a cycle of nodes [2,1]. Thus answer for the first query is 2. We delete the added edge.

Constraints

  • 2 <= n <= 30
  • m == queries.length
  • 1 <= m <= 10^5
  • queries[i].length == 2
  • 1 <= ai, bi <= 2n - 1
  • ai != bi

Solution

Method 1 – Binary Lifting to Find LCA (Lowest Common Ancestor)

Intuition

The key idea is that in a complete binary tree, the path from any node to the root can be found by repeatedly dividing by 2 (moving to the parent). The cycle formed by adding an edge between two nodes is the path from one node to the other via their lowest common ancestor (LCA), plus the added edge. The length of the cycle is the distance from a to lca plus the distance from b to lca, plus 1 (for the added edge).

Approach

  1. For each query [a, b]:
    • Initialize a counter for the path length.
    • While a and b are not equal:
      • If a > b, move a to its parent (a //= 2), increment the counter.
      • Else, move b to its parent (b //= 2), increment the counter.
    • When a == b, both have reached their LCA. Add 1 to the counter (for the added edge).
  2. Return the list of cycle lengths for all queries.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
public:
    vector<int> cycleLengthQueries(int n, vector<vector<int>>& queries) {
        vector<int> ans;
        for (auto& q : queries) {
            int a = q[0], b = q[1], cnt = 0;
            while (a != b) {
                if (a > b) a /= 2;
                else b /= 2;
                ++cnt;
            }
            ans.push_back(cnt + 1);
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

func cycleLengthQueries(n int, queries [][]int) []int {
    ans := make([]int, len(queries))
    for i, q := range queries {
        a, b, cnt := q[0], q[1], 0
        for a != b {
            if a > b {
                a /= 2
            } else {
                b /= 2
            }
            cnt++
        }
        ans[i] = cnt + 1
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class Solution {
    public int[] cycleLengthQueries(int n, int[][] queries) {
        int[] ans = new int[queries.length];
        for (int i = 0; i < queries.length; i++) {
            int a = queries[i][0], b = queries[i][1], cnt = 0;
            while (a != b) {
                if (a > b) a /= 2;
                else b /= 2;
                cnt++;
            }
            ans[i] = cnt + 1;
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution {
    fun cycleLengthQueries(n: Int, queries: Array<IntArray>): IntArray {
        return queries.map { (a0, b0) ->
            var a = a0; var b = b0; var cnt = 0
            while (a != b) {
                if (a > b) a /= 2 else b /= 2
                cnt++
            }
            cnt + 1
        }.toIntArray()
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution:
    def cycleLengthQueries(self, n: int, queries: list[list[int]]) -> list[int]:
        ans = []
        for a, b in queries:
            cnt = 0
            while a != b:
                if a > b:
                    a //= 2
                else:
                    b //= 2
                cnt += 1
            ans.append(cnt + 1)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

impl Solution {
    pub fn cycle_length_queries(_n: i32, queries: Vec<Vec<i32>>) -> Vec<i32> {
        queries.iter().map(|q| {
            let (mut a, mut b) = (q[0], q[1]);
            let mut cnt = 0;
            while a != b {
                if a > b { a /= 2; } else { b /= 2; }
                cnt += 1;
            }
            cnt + 1
        }).collect()
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Solution {
    cycleLengthQueries(n: number, queries: number[][]): number[] {
        return queries.map(([a, b]) => {
            let cnt = 0;
            while (a !== b) {
                if (a > b) a = Math.floor(a / 2);
                else b = Math.floor(b / 2);
                cnt++;
            }
            return cnt + 1;
        });
    }
}

Complexity

  • ⏰ Time complexity: O(m log n), where m is the number of queries and n is the number of nodes. Each query takes O(log n) steps to reach the LCA.
  • 🧺 Space complexity: O(1) (excluding output), as only a few variables are used per query.