Cyclically Rotating a Grid
Problem
You are given an m x n integer matrix grid, where m and n are both
even integers, and an integer k.
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:
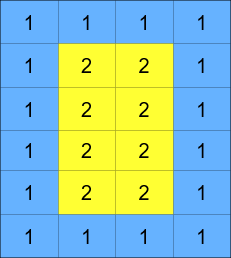
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:
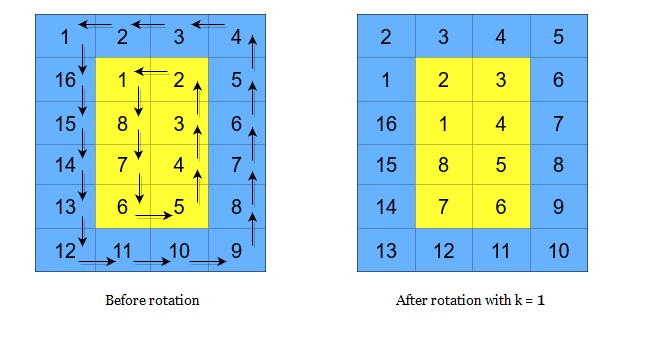
Return the matrix after applyingk cyclic rotations to it.
Examples
Example 1
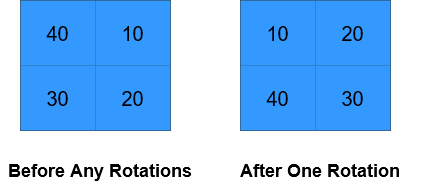
Input: grid = [[40,10],[30,20]], k = 1
Output: [[10,20],[40,30]]
Explanation: The figures above represent the grid at every state.
Example 2
**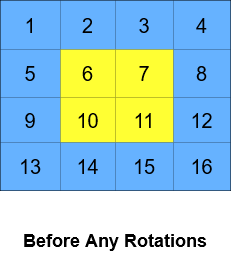****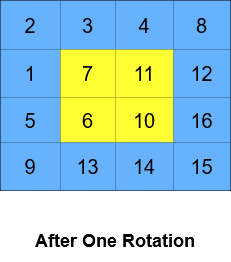****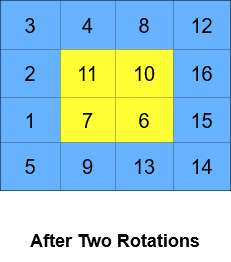**
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
Explanation: The figures above represent the grid at every state.
Constraints
m == grid.lengthn == grid[i].length2 <= m, n <= 50- Both
mandnare even integers. 1 <= grid[i][j] <= 50001 <= k <= 10^9
Solution
Method 1 – Layer Extraction and Rotation
Intuition
The key idea is to treat each layer (ring) of the grid as a 1D array, rotate it by k positions, and then write it back to the grid. This is efficient because the number of layers is small and each layer can be rotated independently.
Approach
- For each layer (from outermost to innermost):
- Extract the elements of the layer into a 1D list in traversal order (top, right, bottom, left).
- Rotate the list by k positions (modulo the layer's length).
- Write the rotated values back into the grid in the same order.
- Repeat for all layers.
- Return the modified grid.
Code
C++
class Solution {
public:
vector<vector<int>> rotateGrid(vector<vector<int>>& grid, int k) {
int m = grid.size(), n = grid[0].size();
int layers = min(m, n) / 2;
for (int l = 0; l < layers; ++l) {
vector<int> vals;
int x1 = l, y1 = l, x2 = m - l - 1, y2 = n - l - 1;
// top
for (int j = y1; j < y2; ++j) vals.push_back(grid[x1][j]);
// right
for (int i = x1; i < x2; ++i) vals.push_back(grid[i][y2]);
// bottom
for (int j = y2; j > y1; --j) vals.push_back(grid[x2][j]);
// left
for (int i = x2; i > x1; --i) vals.push_back(grid[i][y1]);
int len = vals.size();
int rot = k % len;
vector<int> rot_vals(len);
for (int i = 0; i < len; ++i) rot_vals[i] = vals[(i + rot) % len];
int idx = 0;
for (int j = y1; j < y2; ++j) grid[x1][j] = rot_vals[idx++];
for (int i = x1; i < x2; ++i) grid[i][y2] = rot_vals[idx++];
for (int j = y2; j > y1; --j) grid[x2][j] = rot_vals[idx++];
for (int i = x2; i > x1; --i) grid[i][y1] = rot_vals[idx++];
}
return grid;
}
};
Go
func rotateGrid(grid [][]int, k int) [][]int {
m, n := len(grid), len(grid[0])
layers := min(m, n) / 2
for l := 0; l < layers; l++ {
x1, y1, x2, y2 := l, l, m-l-1, n-l-1
vals := []int{}
for j := y1; j < y2; j++ { vals = append(vals, grid[x1][j]) }
for i := x1; i < x2; i++ { vals = append(vals, grid[i][y2]) }
for j := y2; j > y1; j-- { vals = append(vals, grid[x2][j]) }
for i := x2; i > x1; i-- { vals = append(vals, grid[i][y1]) }
ln := len(vals)
rot := k % ln
rotVals := make([]int, ln)
for i := 0; i < ln; i++ { rotVals[i] = vals[(i+rot)%ln] }
idx := 0
for j := y1; j < y2; j++ { grid[x1][j] = rotVals[idx]; idx++ }
for i := x1; i < x2; i++ { grid[i][y2] = rotVals[idx]; idx++ }
for j := y2; j > y1; j-- { grid[x2][j] = rotVals[idx]; idx++ }
for i := x2; i > x1; i-- { grid[i][y1] = rotVals[idx]; idx++ }
}
return grid
}
Java
class Solution {
public int[][] rotateGrid(int[][] grid, int k) {
int m = grid.length, n = grid[0].length;
int layers = Math.min(m, n) / 2;
for (int l = 0; l < layers; l++) {
int x1 = l, y1 = l, x2 = m - l - 1, y2 = n - l - 1;
List<Integer> vals = new ArrayList<>();
for (int j = y1; j < y2; j++) vals.add(grid[x1][j]);
for (int i = x1; i < x2; i++) vals.add(grid[i][y2]);
for (int j = y2; j > y1; j--) vals.add(grid[x2][j]);
for (int i = x2; i > x1; i--) vals.add(grid[i][y1]);
int len = vals.size();
int rot = k % len;
List<Integer> rotVals = new ArrayList<>(Collections.nCopies(len, 0));
for (int i = 0; i < len; i++) rotVals.set(i, vals.get((i + rot) % len));
int idx = 0;
for (int j = y1; j < y2; j++) grid[x1][j] = rotVals.get(idx++);
for (int i = x1; i < x2; i++) grid[i][y2] = rotVals.get(idx++);
for (int j = y2; j > y1; j--) grid[x2][j] = rotVals.get(idx++);
for (int i = x2; i > x1; i--) grid[i][y1] = rotVals.get(idx++);
}
return grid;
}
}
Kotlin
class Solution {
fun rotateGrid(grid: Array<IntArray>, k: Int): Array<IntArray> {
val m = grid.size
val n = grid[0].size
val layers = minOf(m, n) / 2
for (l in 0 until layers) {
val x1 = l; val y1 = l; val x2 = m - l - 1; val y2 = n - l - 1
val vals = mutableListOf<Int>()
for (j in y1 until y2) vals.add(grid[x1][j])
for (i in x1 until x2) vals.add(grid[i][y2])
for (j in y2 downTo y1 + 1) vals.add(grid[x2][j])
for (i in x2 downTo x1 + 1) vals.add(grid[i][y1])
val len = vals.size
val rot = k % len
val rotVals = List(len) { vals[(it + rot) % len] }
var idx = 0
for (j in y1 until y2) grid[x1][j] = rotVals[idx++]
for (i in x1 until x2) grid[i][y2] = rotVals[idx++]
for (j in y2 downTo y1 + 1) grid[x2][j] = rotVals[idx++]
for (i in x2 downTo x1 + 1) grid[i][y1] = rotVals[idx++]
}
return grid
}
}
Python
class Solution:
def rotateGrid(self, grid: list[list[int]], k: int) -> list[list[int]]:
m, n = len(grid), len(grid[0])
layers = min(m, n) // 2
for l in range(layers):
x1, y1, x2, y2 = l, l, m-l-1, n-l-1
vals = []
for j in range(y1, y2): vals.append(grid[x1][j])
for i in range(x1, x2): vals.append(grid[i][y2])
for j in range(y2, y1, -1): vals.append(grid[x2][j])
for i in range(x2, x1, -1): vals.append(grid[i][y1])
ln = len(vals)
rot = k % ln
rot_vals = [vals[(i+rot)%ln] for i in range(ln)]
idx = 0
for j in range(y1, y2): grid[x1][j] = rot_vals[idx]; idx += 1
for i in range(x1, x2): grid[i][y2] = rot_vals[idx]; idx += 1
for j in range(y2, y1, -1): grid[x2][j] = rot_vals[idx]; idx += 1
for i in range(x2, x1, -1): grid[i][y1] = rot_vals[idx]; idx += 1
return grid
Rust
impl Solution {
pub fn rotate_grid(mut grid: Vec<Vec<i32>>, k: i32) -> Vec<Vec<i32>> {
let m = grid.len();
let n = grid[0].len();
let layers = m.min(n) / 2;
for l in 0..layers {
let (x1, y1, x2, y2) = (l, l, m-l-1, n-l-1);
let mut vals = vec![];
for j in y1..y2 { vals.push(grid[x1][j]); }
for i in x1..x2 { vals.push(grid[i][y2]); }
for j in (y1+1..=y2).rev() { vals.push(grid[x2][j]); }
for i in (x1+1..=x2).rev() { vals.push(grid[i][y1]); }
let len = vals.len();
let rot = (k as usize) % len;
let rot_vals: Vec<_> = (0..len).map(|i| vals[(i+rot)%len]).collect();
let mut idx = 0;
for j in y1..y2 { grid[x1][j] = rot_vals[idx]; idx += 1; }
for i in x1..x2 { grid[i][y2] = rot_vals[idx]; idx += 1; }
for j in (y1+1..=y2).rev() { grid[x2][j] = rot_vals[idx]; idx += 1; }
for i in (x1+1..=x2).rev() { grid[i][y1] = rot_vals[idx]; idx += 1; }
}
grid
}
}
TypeScript
class Solution {
rotateGrid(grid: number[][], k: number): number[][] {
const m = grid.length, n = grid[0].length, layers = Math.min(m, n) >> 1;
for (let l = 0; l < layers; l++) {
const x1 = l, y1 = l, x2 = m - l - 1, y2 = n - l - 1;
const vals: number[] = [];
for (let j = y1; j < y2; j++) vals.push(grid[x1][j]);
for (let i = x1; i < x2; i++) vals.push(grid[i][y2]);
for (let j = y2; j > y1; j--) vals.push(grid[x2][j]);
for (let i = x2; i > x1; i--) vals.push(grid[i][y1]);
const len = vals.length, rot = k % len;
const rotVals = Array(len);
for (let i = 0; i < len; i++) rotVals[i] = vals[(i + rot) % len];
let idx = 0;
for (let j = y1; j < y2; j++) grid[x1][j] = rotVals[idx++];
for (let i = x1; i < x2; i++) grid[i][y2] = rotVals[idx++];
for (let j = y2; j > y1; j--) grid[x2][j] = rotVals[idx++];
for (let i = x2; i > x1; i--) grid[i][y1] = rotVals[idx++];
}
return grid;
}
}
Complexity
- ⏰ Time complexity:
O(mn), as each cell is visited a constant number of times. - 🧺 Space complexity:
O(mn), for the temporary arrays used for each layer.