Delete in a Binary Search Tree

Problem

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

1. Search for a node to remove.
2. If the node is found, delete the node.

Examples

Example 1:

Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.

Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

Solution

Method 1 - Recursive + Finding inorder predecessor and successor

This operation is complicated than Find() and Insert() operations. Here we have to deal with 3 cases:

• Node to be deleted is a leaf node ( No Children).
• Node to be deleted has only one child.
• Node to be deleted has two childrens.

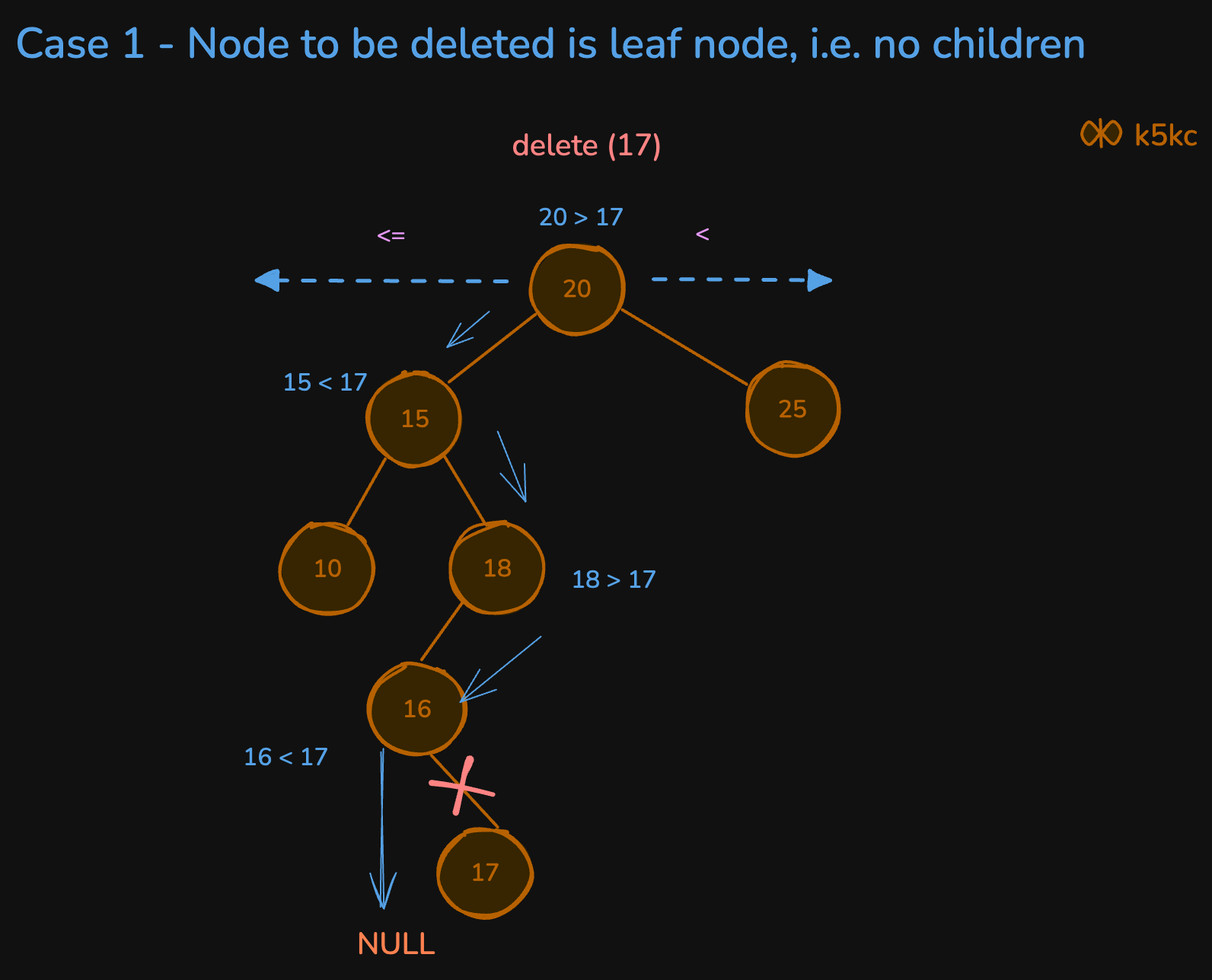
Node to Be Deleted is a Leaf Node (No Children)

its a very simple case, if a node to be deleted has no children then just traverse to that node, keep track of parent node and the side in which the node exist(left or right) and set parent.left = null or parent.right = null;

For eg. delete(root, 17)

Node to Be Deleted Has Only One Child

• Its a slightly complex case. if a node to be deleted(deleteNode) has only one child then just traverse to that node, keep track of parent node and the side in which the node exist(left or right).
• Check which side child is null (since it has only one child).
• Say node to be deleted has child on its left side . Then take the entire sub tree from the left side and add it to the parent and the side on which deleteNode exist, see step 1 and example.

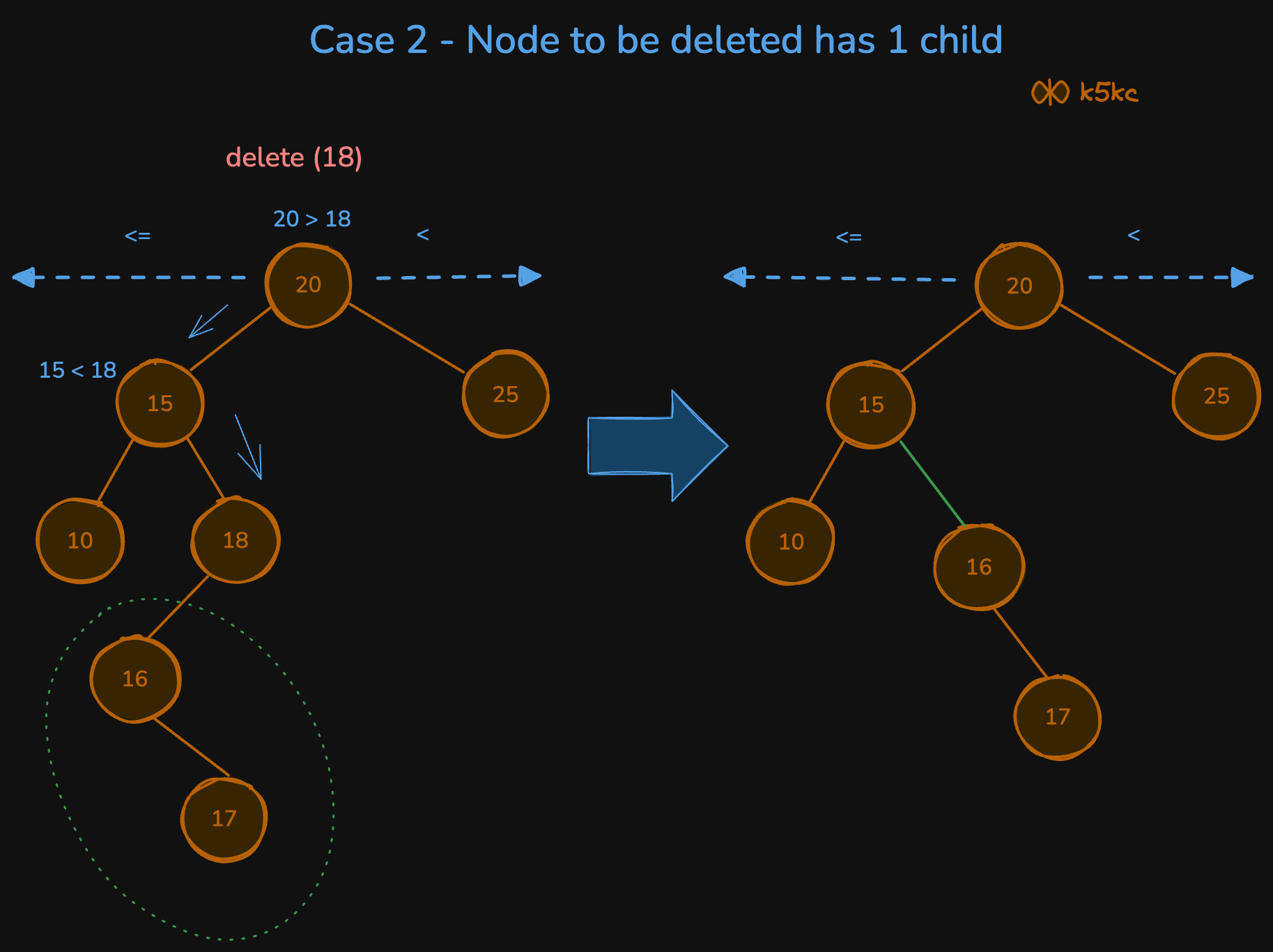For eg. delete(root, 18)

Node to Be Deleted Has Two Childrens

Now this is quite exciting. You just cannot replace the deleteNode with any of its child, Why? Lets try out a example.

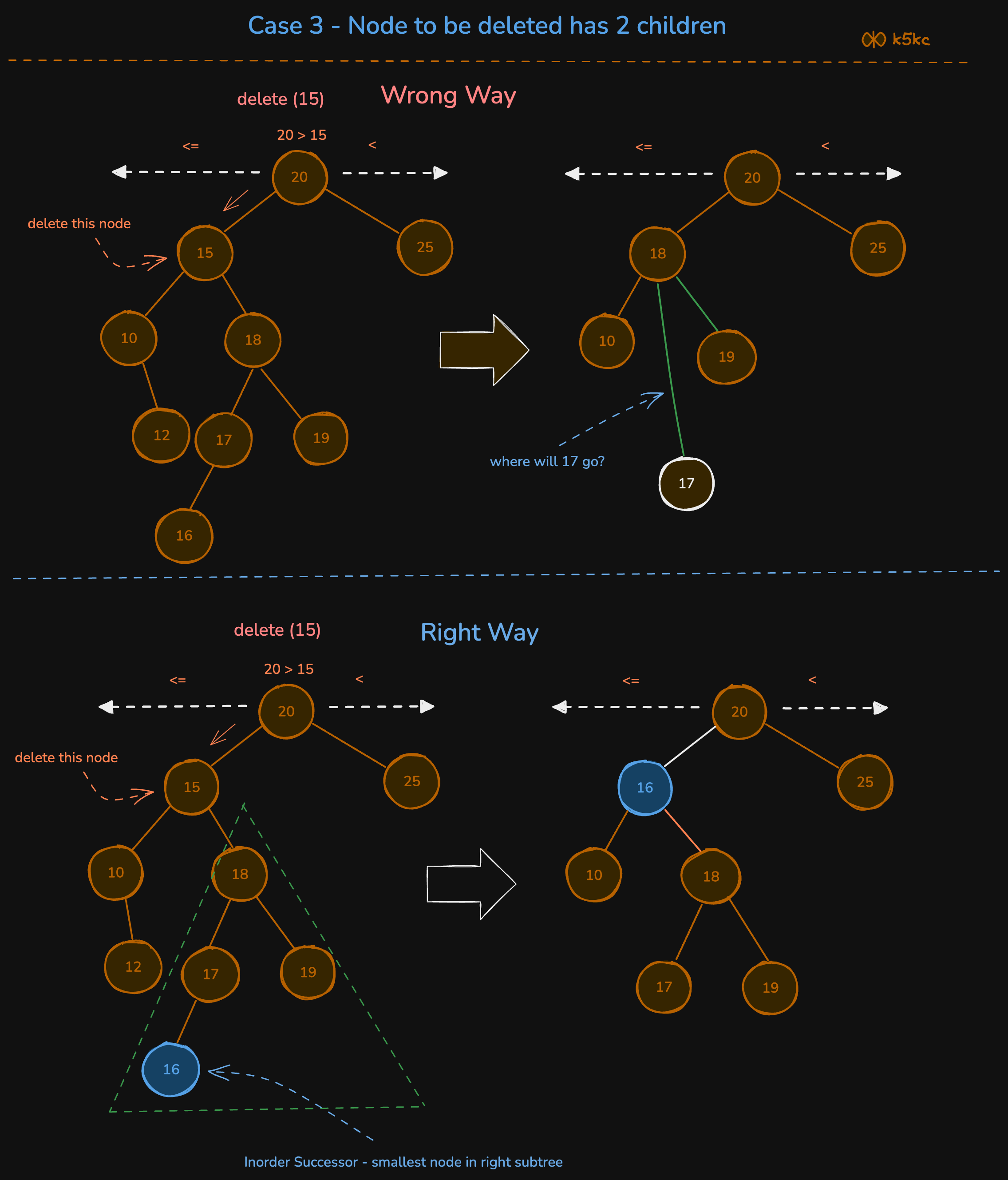
Solution is to find the inorder successor.

• We need to find the [inorder successor](inorder-successor-in-binary-search-tree) of the node to be deleted. Inorder successor in BST is the minimum node just larger than the current node.
• The data of the inorder successor must be copied into the node to be deleted and a pointer should be setup to the inorder successor. This inorder successor would have one right child or zero children in case it is a leaf.
• This inorder node should be deleted using the same procedure as for deleting a one child or a zero child node.

Code

Java

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null; // Base case: Node not found
        }
        
        if (key < root.val) {
            root.left = deleteNode(root.left, key); // Traverse left subtree
        } else if (key > root.val) {
            root.right = deleteNode(root.right, key); // Traverse right subtree
        } else {
            // Node found - proceed with deletion
            if (root.left == null) {
                return root.right; // Case: No left child
            } else if (root.right == null) {
                return root.left; // Case: No right child
            } else {
                // Case: Two children
                TreeNode successor = findMin(root.right); // Find inorder successor
                root.val = successor.val; // Replace with successor value
                root.right = deleteNode(root.right, successor.val); // Delete successor
            }
        }
        return root; // Return updated subtree
    }

    private TreeNode findMin(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node; // Smallest value in the subtree
    }
}

Python

class Solution:
    def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
        if not root:
            return None  # Base Case: Node not found
        
        if key < root.val:
            root.left = self.deleteNode(root.left, key)  # Traverse left subtree
        elif key > root.val:
            root.right = self.deleteNode(root.right, key)  # Traverse right subtree
        else:
            # Node found - proceed with deletion
            if not root.left:
                return root.right  # Case: No left child
            elif not root.right:
                return root.left  # Case: No right child
            else:
                # Case: Two children
                successor = self.findMin(root.right)  # Find inorder successor
                root.val = successor.val  # Replace with successor value
                root.right = self.deleteNode(root.right, successor.val)  # Delete successor
        
        return root  # Return updated subtree

    def findMin(self, node: TreeNode) -> TreeNode:
        while node.left:
            node = node.left
        return node  # Smallest value in the subtree

Complexity

• ⏰ Time complexity: O(log n) for balanced BST; O(n) for skewed BST.
• 🧺 Space complexity:  O(h) due to recursive calls.

Method 2 - Iterative

Code

Java

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        TreeNode parent = null, curr = root;
        
        // Step 1: Search for the node to delete
        while (curr != null && curr.val != key) {
            parent = curr;
            if (key < curr.val) {
                curr = curr.left; // Traverse left subtree
            } else {
                curr = curr.right; // Traverse right subtree
            }
        }
        
        // If the node is not found, return root
        if (curr == null) {
            return root;
        }
        
        // Step 2: Handle deletion cases
        if (curr.left == null || curr.right == null) {
            // Case: Node with one child or no children
            TreeNode child = (curr.left != null) ? curr.left : curr.right;
            
            // If the node to delete is the root, update root
            if (parent == null) {
                return child;
            } 
            
            // Update parent's reference
            if (parent.left == curr) {
                parent.left = child;
            } else {
                parent.right = child;
            }
        } else {
            // Case: Node with two children
            // Find inorder successor
            TreeNode successorParent = curr;
            TreeNode successor = curr.right;
            
            while (successor.left != null) {
                successorParent = successor;
                successor = successor.left; // Find the smallest node in the right subtree
            }
            
            curr.val = successor.val; // Replace node's value with successor's value
            
            // Delete the successor
            if (successorParent.left == successor) {
                successorParent.left = successor.right;
            } else {
                successorParent.right = successor.right;
            }
        }
        
        return root;
    }
}

Python

class TreeNode:
    def __init__(self, val: int = 0, left: Optional['TreeNode'] = None, right: Optional['TreeNode'] = None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
        parent, curr = None, root
        
        # Step 1: Search for the node to delete
        while curr and curr.val != key:
            parent = curr
            if key < curr.val:
                curr = curr.left  # Traverse left subtree
            else:
                curr = curr.right  # Traverse right subtree
        
        # If the node is not found, return root
        if not curr:
            return root
        
        # Step 2: Handle deletion cases
        if not curr.left or not curr.right:
            # Case: Node with one child or no children
            child = curr.left if curr.left else curr.right
            
            # If the node to delete is the root, update root
            if not parent:
                return child
            
            # Update parent's reference
            if parent.left == curr:
                parent.left = child
            else:
                parent.right = child
        else:
            # Case: Node with two children
            # Find inorder successor
            successor_parent = curr
            successor = curr.right
            
            while successor.left:
                successor_parent = successor
                successor = successor.left  # Find the smallest node in the right subtree
            
            curr.val = successor.val  # Replace node's value with successor's value
            
            # Delete the successor
            if successor_parent.left == successor:
                successor_parent.left = successor.right
            else:
                successor_parent.right = successor.right
        
        return root

Complexity

• ⏰ Time complexity: O(h)
• 🧺 Space complexity: O(1)