Delete Tree Nodes

Problem

A tree rooted at node 0 is given as follows:

• The number of nodes is nodes;
• The value of the ith node is value[i];
• The parent of the ith node is parent[i].

Remove every subtree whose sum of values of nodes is zero.

Return the number of the remaining nodes in the tree.

Examples

Example 1:

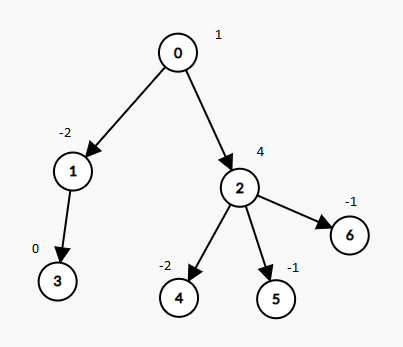
Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-1]
Output: 2

Example 2:

Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-2]
Output: 6

Constraints:

• 1 <= nodes <= 10^4
• parent.length == nodes
• 0 <= parent[i] <= nodes - 1
• parent[0] == -1 which indicates that 0 is the root.
• value.length == nodes
• -10^5 <= value[i] <= 10^5
• The given input is guaranteed to represent a valid tree.

Solution

Method 1 – Post-order DFS to Compute Subtree Sums and Sizes

Intuition

We can use a post-order DFS to compute the sum of values and the size (number of nodes) for each subtree. If a subtree's sum is zero, we remove it (do not count its nodes). Otherwise, we keep its nodes. This approach efficiently traverses the tree and handles deletions in a single pass.

Approach

1. Build the tree as an adjacency list from the parent array.
2. Define a recursive DFS function that returns the sum and size of the subtree rooted at a node.
3. For each node, recursively compute the sum and size of its children.
4. If the total sum of the subtree is zero, return (0, 0) to indicate removal.
5. Otherwise, return (sum, size) including the current node.
6. The answer is the size returned for the root node.

Code

C++

class Solution {
public:
    int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
        vector<vector<int>> g(nodes);
        for (int i = 1; i < nodes; ++i) g[parent[i]].push_back(i);
        function<pair<int, int>(int)> dfs = [&](int u) -> pair<int, int> {
            int sum = value[u], sz = 1;
            for (int v : g[u]) {
                auto [s, cnt] = dfs(v);
                sum += s;
                sz += cnt;
            }
            if (sum == 0) return {0, 0};
            return {sum, sz};
        };
        return dfs(0).second;
    }
};

Go

func deleteTreeNodes(nodes int, parent []int, value []int) int {
    g := make([][]int, nodes)
    for i := 1; i < nodes; i++ {
        g[parent[i]] = append(g[parent[i]], i)
    }
    var dfs func(u int) (int, int)
    dfs = func(u int) (int, int) {
        sum, sz := value[u], 1
        for _, v := range g[u] {
            s, cnt := dfs(v)
            sum += s
            sz += cnt
        }
        if sum == 0 {
            return 0, 0
        }
        return sum, sz
    }
    _, ans := dfs(0)
    return ans
}

Java

class Solution {
    public int deleteTreeNodes(int nodes, int[] parent, int[] value) {
        List<Integer>[] g = new List[nodes];
        for (int i = 0; i < nodes; i++) g[i] = new ArrayList<>();
        for (int i = 1; i < nodes; i++) g[parent[i]].add(i);
        int[] ans = dfs(0, g, value);
        return ans[1];
    }
    private int[] dfs(int u, List<Integer>[] g, int[] value) {
        int sum = value[u], sz = 1;
        for (int v : g[u]) {
            int[] res = dfs(v, g, value);
            sum += res[0];
            sz += res[1];
        }
        if (sum == 0) return new int[]{0, 0};
        return new int[]{sum, sz};
    }
}

Kotlin

class Solution {
    fun deleteTreeNodes(nodes: Int, parent: IntArray, value: IntArray): Int {
        val g = Array(nodes) { mutableListOf<Int>() }
        for (i in 1 until nodes) g[parent[i]].add(i)
        fun dfs(u: Int): Pair<Int, Int> {
            var sum = value[u]
            var sz = 1
            for (v in g[u]) {
                val (s, cnt) = dfs(v)
                sum += s
                sz += cnt
            }
            return if (sum == 0) 0 to 0 else sum to sz
        }
        return dfs(0).second
    }
}

Python

class Solution:
    def deleteTreeNodes(self, nodes: int, parent: list[int], value: list[int]) -> int:
        g: list[list[int]] = [[] for _ in range(nodes)]
        for i in range(1, nodes):
            g[parent[i]].append(i)
        def dfs(u: int) -> tuple[int, int]:
            s, sz = value[u], 1
            for v in g[u]:
                cs, csz = dfs(v)
                s += cs
                sz += csz
            if s == 0:
                return 0, 0
            return s, sz
        return dfs(0)[1]

Rust

impl Solution {
    pub fn delete_tree_nodes(nodes: i32, parent: Vec<i32>, value: Vec<i32>) -> i32 {
        let nodes = nodes as usize;
        let mut g = vec![vec![]; nodes];
        for i in 1..nodes {
            g[parent[i] as usize].push(i);
        }
        fn dfs(u: usize, g: &Vec<Vec<usize>>, value: &Vec<i32>) -> (i32, i32) {
            let mut sum = value[u];
            let mut sz = 1;
            for &v in &g[u] {
                let (s, cnt) = dfs(v, g, value);
                sum += s;
                sz += cnt;
            }
            if sum == 0 { (0, 0) } else { (sum, sz) }
        }
        dfs(0, &g, &value).1
    }
}

TypeScript

class Solution {
    deleteTreeNodes(nodes: number, parent: number[], value: number[]): number {
        const g: number[][] = Array.from({length: nodes}, () => []);
        for (let i = 1; i < nodes; i++) g[parent[i]].push(i);
        function dfs(u: number): [number, number] {
            let sum = value[u], sz = 1;
            for (const v of g[u]) {
                const [s, cnt] = dfs(v);
                sum += s;
                sz += cnt;
            }
            if (sum === 0) return [0, 0];
            return [sum, sz];
        }
        return dfs(0)[1];
    }
}

Complexity

• ⏰ Time complexity: O(n), where n is the number of nodes, since each node is visited once.
• 🧺 Space complexity: O(n), for the adjacency list and recursion stack.