Describe the Painting

Problem

There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a unique color. You are given a 2D integer array segments, where segments[i] = [starti, endi, colori] represents the half-closed segment [starti, endi) with colori as the color.

The colors in the overlapping segments of the painting were mixed when it was painted. When two or more colors mix, they form a new color that can be represented as a set of mixed colors.

For example, if colors 2, 4, and 6 are mixed, then the resulting mixed color is {2,4,6}.

For the sake of simplicity, you should only output the sum of the elements in the set rather than the full set.

You want to describe the painting with the minimum number of non-overlapping half-closed segments of these mixed colors. These segments can be represented by the 2D array painting where painting[j] = [leftj, rightj, mixj] describes a half-closed segment [leftj, rightj) with the mixed color sum of mixj.

For example, the painting created with segments = [[1,4,5],[1,7,7]] can be described by painting = [[1,4,12],[4,7,7]] because:
- [1,4) is colored {5,7} (with a sum of 12) from both the first and second segments.
- [4,7) is colored {7} from only the second segment.

Return the 2D array painting describing the finished painting (excluding any parts that are not painted). You may return the segments in any order.

A half-closed segment [a, b) is the section of the number line between points a and b including point a and not including point b.

Examples

Example 1:

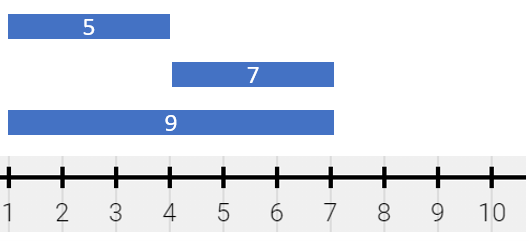
Input: segments = [[1,4,5],[4,7,7],[1,7,9]]
Output: [[1,4,14],[4,7,16]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- [4,7) is colored {7,9} (with a sum of 16) from the second and third segments.

Example 2:

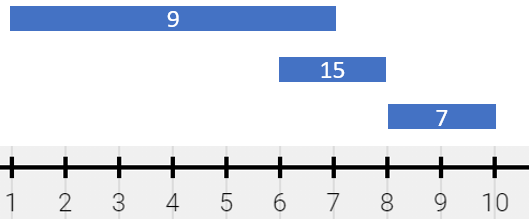
Input: segments = [[1,7,9],[6,8,15],[8,10,7]]
Output: [[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
Explanation: The painting can be described as follows:
- [1,6) is colored 9 from the first segment.
- [6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- [7,8) is colored 15 from the second segment.
- [8,10) is colored 7 from the third segment.

Example 3:

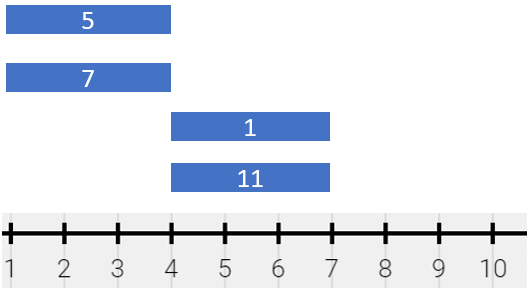
Input: segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
Output: [[1,4,12],[4,7,12]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- [4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment [1,7) is incorrect because the mixed color sets are different.

Constraints:

1 <= segments.length <= 2 * 10^4
segments[i].length == 3
1 <= starti < endi <= 10^5
1 <= colori <= 10^9
Each colori is distinct.

Solution

Method 1 - Sweep line algorithm

The key idea for solving this problem is to merge intervals based on the colors applied and create new non-overlapping intervals with their mixed color sums:

Use sweep line and sort events to determine the intervals where color changes.
Events represent a starting or ending of a segment. For each segment [start, end, color], you add two events:
- A start event for start with color.
- An end event for end to remove color.
Traverse the sorted events and keep track of the active colors using a TreeMap or ordered map in Java and Python.
Whenever moving between events on the number line, output the interval [left, right) and sum of active color set values.
Finally, return the result.

Code

Java

class Solution {

    public List<List<Integer>> splitPainting(int[][] segments) {
        // Step 1: Create a TreeMap to store events
        TreeMap<Integer, Integer> events = new TreeMap<>();
        for (int[] seg : segments) {
            int start = seg[0], end = seg[1], color = seg[2];
            // Start event
            events.put(start, events.getOrDefault(start, 0) + color);
            // End event
            events.put(end, events.getOrDefault(end, 0) - color);
        }

        // Step 2: Process events to construct intervals
        List<List<Integer>> ans = new ArrayList<>();
        int prev = -1; // Previous position on the number line
        int currSum = 0; // Current sum of colors
        for (Map.Entry<Integer, Integer> entry : events.entrySet()) {
            int pos = entry.getKey();
            int color = entry.getValue();

            // If we are moving to a new position in the number line
            if (prev != -1 && currSum != 0) {
                ans.add(Arrays.asList(prev, pos, currSum));
            }

            // Update sum of colors
            currSum += color;
            prev = pos;
        }

        return ans;
    }
}

Python

class Solution:
    def splitPainting(self, segments: List[List[int]]) -> List[List[int]]:
        # Step 1: Create a list of events
        events = []
        for s, e, c in segments:
            events.append((s, c))  # Starting event
            events.append((e, -c))  # Ending event

        # Step 2: Sort events by position
        events.sort()

        # Step 3: Process events to construct intervals
        ans = []  # Final result
        prev = None  # Previous position
        curr_sum = 0  # Current sum of colors
        for i in range(len(events)):
            pos, color = events[i]

            # If we are moving to a new position in the number line
            if prev is not None and pos != prev:
                # Add interval to `ans` if the sum is non-zero (paint exists)
                if curr_sum != 0:
                    ans.append([prev, pos, curr_sum])

            # Update sum of colors
            curr_sum += color
            prev = pos

        return ans

Complexity

⏰ Time complexity: O(n log n)
- Sorting the events: O(n log n), where n is the number of segments.
- Traversing events and managing active colors: O(n). Overall complexity is O(n log n).
🧺 Space complexity: O(n) for storing events and active colors.