Problem

There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [fromi, toi, edgeCosti] meaning that there is an edge from fromi to toi with the cost edgeCosti.

Implement the Graph class:

  • Graph(int n, int[][] edges) initializes the object with n nodes and the given edges.
  • addEdge(int[] edge) adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.
  • int shortestPath(int node1, int node2) returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

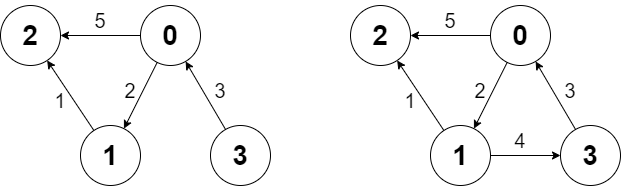
**Input**
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
**Output**
[null, 6, -1, null, 6]

**Explanation**
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6.
g.shortestPath(0, 3); // return -1. There is no path from 0 to 3.
g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above.
g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.

Solution

Method 1 – Dijkstra’s Algorithm with Adjacency List

Intuition

To efficiently find the shortest path in a directed weighted graph, we use Dijkstra’s algorithm. This algorithm explores nodes in order of increasing path cost, always expanding the least costly path first. By maintaining an adjacency list, we can quickly access neighbors and update path costs as we traverse the graph.

Approach

  1. Store the graph as an adjacency list, where each node maps to a list of (neighbor, cost) pairs.
  2. For shortestPath, use a min-heap to always expand the node with the lowest current cost.
  3. Track the minimum cost to reach each node using a distance array or map.
  4. When adding an edge, update the adjacency list.
  5. If the destination is reached, return the cost; if not reachable, return -1.

Complexity

  • ⏰ Time complexity: O(E log V), where E is the number of edges and V is the number of nodes, due to heap operations in Dijkstra’s algorithm.
  • 🧺 Space complexity: O(E + V), for storing the adjacency list and heap.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
class Graph {
    vector<vector<pair<int, int>>> adj;
public:
    Graph(int n, vector<vector<int>>& edges) {
        adj.resize(n);
        for (auto& e : edges) adj[e[0]].emplace_back(e[1], e[2]);
    }
    void addEdge(vector<int> edge) {
        adj[edge[0]].emplace_back(edge[1], edge[2]);
    }
    int shortestPath(int node1, int node2) {
        vector<int> dist(adj.size(), INT_MAX);
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
        dist[node1] = 0;
        pq.emplace(0, node1);
        while (!pq.empty()) {
            auto [cost, u] = pq.top(); pq.pop();
            if (u == node2) return cost;
            if (cost > dist[u]) continue;
            for (auto& [v, w] : adj[u]) {
                if (dist[v] > cost + w) {
                    dist[v] = cost + w;
                    pq.emplace(dist[v], v);
                }
            }
        }
        return -1;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import java.util.*;
class Graph {
    private final List<List<int[]>> adjList;
    public Graph(int n, int[][] edges) {
        adjList = new ArrayList<>(n);
        for (int i = 0; i < n; i++) adjList.add(new ArrayList<>());
        for (int[] edge : edges) addEdge(edge);
    }
    public void addEdge(int[] edge) {
        adjList.get(edge[0]).add(new int[]{edge[1], edge[2]});
    }
    public int shortestPath(int node1, int node2) {
        int[] dist = new int[adjList.size()];
        Arrays.fill(dist, Integer.MAX_VALUE);
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        dist[node1] = 0;
        pq.offer(new int[]{0, node1});
        while (!pq.isEmpty()) {
            int[] curr = pq.poll();
            int cost = curr[0], u = curr[1];
            if (u == node2) return cost;
            if (cost > dist[u]) continue;
            for (int[] nei : adjList.get(u)) {
                int v = nei[0], w = nei[1];
                if (dist[v] > cost + w) {
                    dist[v] = cost + w;
                    pq.offer(new int[]{dist[v], v});
                }
            }
        }
        return -1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import heapq
class Graph:
    def __init__(self, n: int, edges: list[list[int]]) -> None:
        self.adj: list[list[tuple[int, int]]] = [[] for _ in range(n)]
        for u, v, w in edges:
            self.adj[u].append((v, w))
    def addEdge(self, edge: list[int]) -> None:
        u, v, w = edge
        self.adj[u].append((v, w))
    def shortestPath(self, node1: int, node2: int) -> int:
        n = len(self.adj)
        dist = [float('inf')] * n
        dist[node1] = 0
        heap = [(0, node1)]
        while heap:
            cost, u = heapq.heappop(heap)
            if u == node2:
                return cost
            if cost > dist[u]:
                continue
            for v, w in self.adj[u]:
                if dist[v] > cost + w:
                    dist[v] = cost + w
                    heapq.heappush(heap, (dist[v], v))
        return -1