problemeasyalgorithmsleetcode-3242leetcode 3242leetcode3242

Design Neighbor Sum Service

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a n x n 2D array grid containing distinct elements in the range [0, n2 - 1].

Implement the NeighborSum class:

  • NeighborSum(int [][]grid) initializes the object.
  • int adjacentSum(int value) returns the sum of elements which are adjacent neighbors of value, that is either to the top, left, right, or bottom of value in grid.
  • int diagonalSum(int value) returns the sum of elements which are diagonal neighbors of value, that is either to the top-left, top-right, bottom-left, or bottom-right of value in grid.

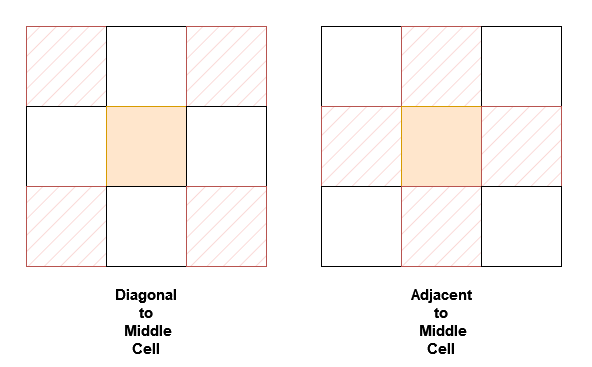
Examples

Example 1


Input:

["NeighborSum", "adjacentSum", "adjacentSum", "diagonalSum", "diagonalSum"]

[[[[0, 1, 2], [3, 4, 5], [6, 7, 8]]], [1], [4], [4], [8]]

Output: [null, 6, 16, 16, 4]

Explanation:

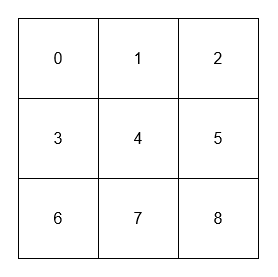**![](https://assets.leetcode.com/uploads/2024/06/24/designexample0.png)**

  * The adjacent neighbors of 1 are 0, 2, and 4.
  * The adjacent neighbors of 4 are 1, 3, 5, and 7.
  * The diagonal neighbors of 4 are 0, 2, 6, and 8.
  * The diagonal neighbor of 8 is 4.

Example 2


Input:

["NeighborSum", "adjacentSum", "diagonalSum"]

[[[[1, 2, 0, 3], [4, 7, 15, 6], [8, 9, 10, 11], [12, 13, 14, 5]]], [15], [9]]

Output: [null, 23, 45]

Explanation:

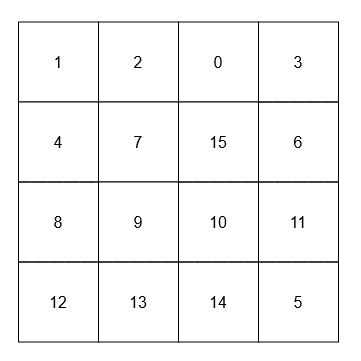**![](https://assets.leetcode.com/uploads/2024/06/24/designexample2.png)**

  * The adjacent neighbors of 15 are 0, 10, 7, and 6.
  * The diagonal neighbors of 9 are 4, 12, 14, and 15.

Constraints

  • 3 <= n == grid.length == grid[0].length <= 10
  • 0 <= grid[i][j] <= n2 - 1
  • All grid[i][j] are distinct.
  • value in adjacentSum and diagonalSum will be in the range [0, n2 - 1].
  • At most 2 * n2 calls will be made to adjacentSum and diagonalSum.

Solution

Method 1 – Precompute Value to Position Map

Intuition

Since all values in the grid are distinct and in a known range, we can precompute a mapping from value to its (row, col) position. This allows O(1) lookup for any value. For each query, we check the 4 adjacent or 4 diagonal directions and sum the valid neighbors.

Approach

  1. On initialization, build a map from value to (row, col) for all grid values.
  2. For adjacentSum(value), get the (row, col) of value, then sum the values at up to 4 adjacent positions (up, down, left, right) if within bounds.
  3. For diagonalSum(value), sum the values at up to 4 diagonal positions (top-left, top-right, bottom-left, bottom-right) if within bounds.
  4. Return the computed sum for each query.

Code

C++
class NeighborSum {
    vector<vector<int>> grid;
    unordered_map<int, pair<int, int>> pos;
    int n;
public:
    NeighborSum(vector<vector<int>>& g) : grid(g), n(g.size()) {
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                pos[grid[i][j]] = {i, j};
    }
    int adjacentSum(int v) {
        auto [i, j] = pos[v];
        int ans = 0;
        vector<pair<int, int>> dirs = {{-1,0},{1,0},{0,-1},{0,1}};
        for (auto [di, dj] : dirs) {
            int ni = i + di, nj = j + dj;
            if (ni >= 0 && ni < n && nj >= 0 && nj < n)
                ans += grid[ni][nj];
        }
        return ans;
    }
    int diagonalSum(int v) {
        auto [i, j] = pos[v];
        int ans = 0;
        vector<pair<int, int>> dirs = {{-1,-1},{-1,1},{1,-1},{1,1}};
        for (auto [di, dj] : dirs) {
            int ni = i + di, nj = j + dj;
            if (ni >= 0 && ni < n && nj >= 0 && nj < n)
                ans += grid[ni][nj];
        }
        return ans;
    }
};
Go
type NeighborSum struct {
    grid [][]int
    pos map[int][2]int
    n int
}
func Constructor(grid [][]int) NeighborSum {
    n := len(grid)
    pos := map[int][2]int{}
    for i := 0; i < n; i++ {
        for j := 0; j < n; j++ {
            pos[grid[i][j]] = [2]int{i, j}
        }
    }
    return NeighborSum{grid, pos, n}
}
func (ns *NeighborSum) AdjacentSum(v int) int {
    p := ns.pos[v]
    i, j := p[0], p[1]
    ans := 0
    dirs := [][2]int{{-1,0},{1,0},{0,-1},{0,1}}
    for _, d := range dirs {
        ni, nj := i+d[0], j+d[1]
        if ni >= 0 && ni < ns.n && nj >= 0 && nj < ns.n {
            ans += ns.grid[ni][nj]
        }
    }
    return ans
}
func (ns *NeighborSum) DiagonalSum(v int) int {
    p := ns.pos[v]
    i, j := p[0], p[1]
    ans := 0
    dirs := [][2]int{{-1,-1},{-1,1},{1,-1},{1,1}}
    for _, d := range dirs {
        ni, nj := i+d[0], j+d[1]
        if ni >= 0 && ni < ns.n && nj >= 0 && nj < ns.n {
            ans += ns.grid[ni][nj]
        }
    }
    return ans
}
Java
public class NeighborSum {
    private int[][] grid;
    private Map<Integer, int[]> pos;
    private int n;
    public NeighborSum(int[][] grid) {
        this.grid = grid;
        n = grid.length;
        pos = new HashMap<>();
        for (int i = 0; i < n; ++i)
            for (int j = 0; j < n; ++j)
                pos.put(grid[i][j], new int[]{i, j});
    }
    public int adjacentSum(int v) {
        int[] p = pos.get(v);
        int i = p[0], j = p[1], ans = 0;
        int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};
        for (int[] d : dirs) {
            int ni = i + d[0], nj = j + d[1];
            if (ni >= 0 && ni < n && nj >= 0 && nj < n)
                ans += grid[ni][nj];
        }
        return ans;
    }
    public int diagonalSum(int v) {
        int[] p = pos.get(v);
        int i = p[0], j = p[1], ans = 0;
        int[][] dirs = {{-1,-1},{-1,1},{1,-1},{1,1}};
        for (int[] d : dirs) {
            int ni = i + d[0], nj = j + d[1];
            if (ni >= 0 && ni < n && nj >= 0 && nj < n)
                ans += grid[ni][nj];
        }
        return ans;
    }
}
Kotlin
class NeighborSum(grid: Array<IntArray>) {
    private val grid = grid
    private val n = grid.size
    private val pos = mutableMapOf<Int, Pair<Int, Int>>()
    init {
        for (i in 0 until n) for (j in 0 until n) pos[grid[i][j]] = i to j
    }
    fun adjacentSum(v: Int): Int {
        val (i, j) = pos[v]!!
        var ans = 0
        val dirs = listOf(-1 to 0, 1 to 0, 0 to -1, 0 to 1)
        for ((di, dj) in dirs) {
            val ni = i + di; val nj = j + dj
            if (ni in 0 until n && nj in 0 until n) ans += grid[ni][nj]
        }
        return ans
    }
    fun diagonalSum(v: Int): Int {
        val (i, j) = pos[v]!!
        var ans = 0
        val dirs = listOf(-1 to -1, -1 to 1, 1 to -1, 1 to 1)
        for ((di, dj) in dirs) {
            val ni = i + di; val nj = j + dj
            if (ni in 0 until n && nj in 0 until n) ans += grid[ni][nj]
        }
        return ans
    }
}
Python
class NeighborSum:
    def __init__(self, grid: list[list[int]]):
        self.grid = grid
        self.n = len(grid)
        self.pos: dict[int, tuple[int, int]] = {}
        for i in range(self.n):
            for j in range(self.n):
                self.pos[grid[i][j]] = (i, j)
    def adjacentSum(self, v: int) -> int:
        i, j = self.pos[v]
        ans = 0
        for di, dj in [(-1,0),(1,0),(0,-1),(0,1)]:
            ni, nj = i+di, j+dj
            if 0 <= ni < self.n and 0 <= nj < self.n:
                ans += self.grid[ni][nj]
        return ans
    def diagonalSum(self, v: int) -> int:
        i, j = self.pos[v]
        ans = 0
        for di, dj in [(-1,-1),(-1,1),(1,-1),(1,1)]:
            ni, nj = i+di, j+dj
            if 0 <= ni < self.n and 0 <= nj < self.n:
                ans += self.grid[ni][nj]
        return ans
Rust
use std::collections::HashMap;
struct NeighborSum {
    grid: Vec<Vec<i32>>,
    pos: HashMap<i32, (usize, usize)>,
    n: usize,
}
impl NeighborSum {
    fn new(grid: Vec<Vec<i32>>) -> Self {
        let n = grid.len();
        let mut pos = HashMap::new();
        for i in 0..n {
            for j in 0..n {
                pos.insert(grid[i][j], (i, j));
            }
        }
        Self { grid, pos, n }
    }
    fn adjacent_sum(&self, v: i32) -> i32 {
        let (i, j) = self.pos[&v];
        let mut ans = 0;
        for (di, dj) in [(-1,0),(1,0),(0,-1),(0,1)] {
            let ni = i as isize + di;
            let nj = j as isize + dj;
            if ni >= 0 && ni < self.n as isize && nj >= 0 && nj < self.n as isize {
                ans += self.grid[ni as usize][nj as usize];
            }
        }
        ans
    }
    fn diagonal_sum(&self, v: i32) -> i32 {
        let (i, j) = self.pos[&v];
        let mut ans = 0;
        for (di, dj) in [(-1,-1),(-1,1),(1,-1),(1,1)] {
            let ni = i as isize + di;
            let nj = j as isize + dj;
            if ni >= 0 && ni < self.n as isize && nj >= 0 && nj < self.n as isize {
                ans += self.grid[ni as usize][nj as usize];
            }
        }
        ans
    }
}
TypeScript
class NeighborSum {
    private grid: number[][];
    private n: number;
    private pos: Map<number, [number, number]>;
    constructor(grid: number[][]) {
        this.grid = grid;
        this.n = grid.length;
        this.pos = new Map();
        for (let i = 0; i < this.n; i++)
            for (let j = 0; j < this.n; j++)
                this.pos.set(grid[i][j], [i, j]);
    }
    adjacentSum(v: number): number {
        const [i, j] = this.pos.get(v)!;
        let ans = 0;
        for (const [di, dj] of [[-1,0],[1,0],[0,-1],[0,1]]) {
            const ni = i + di, nj = j + dj;
            if (ni >= 0 && ni < this.n && nj >= 0 && nj < this.n)
                ans += this.grid[ni][nj];
        }
        return ans;
    }
    diagonalSum(v: number): number {
        const [i, j] = this.pos.get(v)!;
        let ans = 0;
        for (const [di, dj] of [[-1,-1],[-1,1],[1,-1],[1,1]]) {
            const ni = i + di, nj = j + dj;
            if (ni >= 0 && ni < this.n && nj >= 0 && nj < this.n)
                ans += this.grid[ni][nj];
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(1) per query, since all lookups and neighbor checks are constant time.
  • 🧺 Space complexity: O(n^2), for the grid and value-to-position map.

Comments