Detect Cycle in Directed Graph
Problem
Given a directed graph write an algorithm to find out whether graph contains cycle or not.
Examples
Example 1
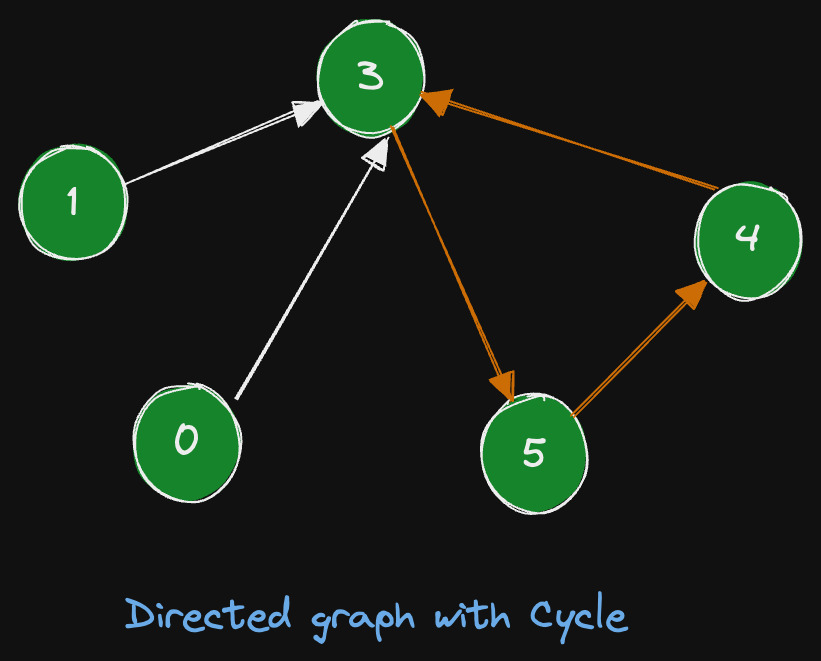
Input: n = 5, edges = [[0,3], [1,3], [3,5], [5,4], [4,3]]
Output: true
Explanation: The graph has a cycle: 3 → 5 → 4 → 3. Starting from node 3, we can traverse to node 5, then to node 4, and finally back to node 3, forming a directed cycle. Nodes 0 and 1 both point to node 3, but they don't affect the cycle detection.
Example 2
Input: n = 4, edges = [[0,1], [1,2], [2,3]]
Output: false
Explanation: This is a simple directed path 0→1→2→3 with no cycles. Each node is visited at most once, and there are no back edges.
Example 3
Input: n = 3, edges = [[0,1], [1,2], [2,0]]
Output: true
Explanation: Triangle cycle: 0 → 1 → 2 → 0. All three nodes form a directed cycle.
Example 4
Input: n = 2, edges = [[0,1], [1,1]]
Output: true
Explanation: Self-loop cycle at node 1. Node 1 has an edge pointing to itself, which creates a cycle.
Solution
Method 1 - DFS
DFS for a connected graph produces a tree. For a disconnected graph, Get the DFS forest as output.
Graph contains cycle if there are any back edges. We have already seen Types of Edges in Graph.
There are two types of back edges as seen in the example above (marked in red)
- Edge from a vertex to itself. Self loop. (4-4)
- Edge from any descendent back to vertex.
To detect a back edge, keep track of vertices currently in the recursion stack recursionStk[] of function for DFS traversal. If a vertex is reached that is already in the recursion stack, then there is a cycle in the tree. The edge that connects the current vertex to the vertex in the recursion stack is a back edge. Use recursionStk[] array to keep track of vertices in the recursion stack.
Algorithm
- Do DFS from every vertex
- For DFS from each vertex, keep track of visiting vertices in a recursion stack
- If you encounter a vertex which is already present in recursion stack then we have found a cycle
- Use
visited[]array to keep track of already visited vertices to avoid redundant work - Use
recursionStack[]array to keep track of vertices currently in the DFS recursion stack
How Different is Recursion Stack From Visited Array?
visited[]is used to keep track of already visited vertices during the entire DFS process and never gets resetrecursionStack[]is used to keep track of visiting vertices during DFS from a particular vertex and gets reset once we backtrack from that vertex- This distinction is crucial for directed graphs as we need to detect back edges within the current DFS path
Code
C++
class Solution {
public:
bool hasCycle(int n, vector<vector<int>>& edges) {
// Build adjacency list
vector<vector<int>> adj(n);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
}
vector<bool> visited(n, false);
vector<bool> recursionStack(n, false);
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, adj, visited, recursionStack)) {
return true;
}
}
}
return false;
}
private:
bool dfs(int u, vector<vector<int>>& adj, vector<bool>& visited, vector<bool>& recursionStack) {
// Mark current node as visited and add to recursion stack
visited[u] = true;
recursionStack[u] = true;
// Visit all adjacent vertices
for (int v : adj[u]) {
if (!visited[v]) {
// If not visited, recurse
if (dfs(v, adj, visited, recursionStack)) {
return true;
}
} else if (recursionStack[v]) {
// If visited and in recursion stack, cycle found
return true;
}
}
// Remove from recursion stack before backtracking
recursionStack[u] = false;
return false;
}
};
Java
class Solution {
public boolean hasCycle(int n, int[][] edges) {
// Build adjacency list
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
}
boolean[] visited = new boolean[n];
boolean[] recursionStack = new boolean[n];
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, adj, visited, recursionStack)) {
return true;
}
}
}
return false;
}
private boolean dfs(int u, List<List<Integer>> adj, boolean[] visited, boolean[] recursionStack) {
// Mark current node as visited and add to recursion stack
visited[u] = true;
recursionStack[u] = true;
// Visit all adjacent vertices
for (int v : adj.get(u)) {
if (!visited[v]) {
// If not visited, recurse
if (dfs(v, adj, visited, recursionStack)) {
return true;
}
} else if (recursionStack[v]) {
// If visited and in recursion stack, cycle found
return true;
}
}
// Remove from recursion stack before backtracking
recursionStack[u] = false;
return false;
}
}
Python
class Solution:
def has_cycle(self, n: int, edges: List[List[int]]) -> bool:
# Build adjacency list
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
visited = [False] * n
recursion_stack = [False] * n
# Check each component
for i in range(n):
if not visited[i]:
if self._dfs(i, adj, visited, recursion_stack):
return True
return False
def _dfs(self, u: int, adj: List[List[int]], visited: List[bool], recursion_stack: List[bool]) -> bool:
# Mark current node as visited and add to recursion stack
visited[u] = True
recursion_stack[u] = True
# Visit all adjacent vertices
for v in adj[u]:
if not visited[v]:
# If not visited, recurse
if self._dfs(v, adj, visited, recursion_stack):
return True
elif recursion_stack[v]:
# If visited and in recursion stack, cycle found
return True
# Remove from recursion stack before backtracking
recursion_stack[u] = False
return False
Complexity
- ⏰ Time complexity:
O(V + E), where V is the number of vertices and E is the number of edges. We visit each vertex once and traverse each edge once - 🧺 Space complexity:
O(V + E), for the adjacency list representation and the recursion stack which can go up to O(V) in the worst case
Method 2 - BFS (Kahn's Algorithm for Topological Sort)
While DFS is the natural approach for cycle detection in directed graphs, we can also use BFS through Kahn's Algorithm for topological sorting. The key insight is that a directed graph has a cycle if and only if it cannot be topologically sorted.
Algorithm
- Calculate in-degree (number of incoming edges) for each vertex
- Add all vertices with in-degree 0 to a queue
- Process vertices from the queue:
- Remove vertex from queue and increment processed count
- For each neighbor, decrease its in-degree by 1
- If neighbor's in-degree becomes 0, add it to queue
- If we processed all vertices, no cycle exists
- If some vertices remain unprocessed, a cycle exists
Code
C++
class Solution {
public:
bool hasCycle(int n, vector<vector<int>>& edges) {
// Build adjacency list and calculate in-degrees
vector<vector<int>> adj(n);
vector<int> inDegree(n, 0);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
inDegree[edge[1]]++;
}
// Add all vertices with in-degree 0 to queue
queue<int> q;
for (int i = 0; i < n; i++) {
if (inDegree[i] == 0) {
q.push(i);
}
}
int processedCount = 0;
// Process vertices using Kahn's algorithm
while (!q.empty()) {
int u = q.front();
q.pop();
processedCount++;
// Reduce in-degree of all neighbors
for (int v : adj[u]) {
inDegree[v]--;
if (inDegree[v] == 0) {
q.push(v);
}
}
}
// If we couldn't process all vertices, cycle exists
return processedCount != n;
}
};
Java
class Solution {
public boolean hasCycle(int n, int[][] edges) {
// Build adjacency list and calculate in-degrees
List<List<Integer>> adj = new ArrayList<>();
int[] inDegree = new int[n];
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
inDegree[edge[1]]++;
}
// Add all vertices with in-degree 0 to queue
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < n; i++) {
if (inDegree[i] == 0) {
queue.offer(i);
}
}
int processedCount = 0;
// Process vertices using Kahn's algorithm
while (!queue.isEmpty()) {
int u = queue.poll();
processedCount++;
// Reduce in-degree of all neighbors
for (int v : adj.get(u)) {
inDegree[v]--;
if (inDegree[v] == 0) {
queue.offer(v);
}
}
}
// If we couldn't process all vertices, cycle exists
return processedCount != n;
}
}
Python
from collections import deque
from typing import List
class Solution:
def has_cycle(self, n: int, edges: List[List[int]]) -> bool:
# Build adjacency list and calculate in-degrees
adj = [[] for _ in range(n)]
in_degree = [0] * n
for u, v in edges:
adj[u].append(v)
in_degree[v] += 1
# Add all vertices with in-degree 0 to queue
queue = deque()
for i in range(n):
if in_degree[i] == 0:
queue.append(i)
processed_count = 0
# Process vertices using Kahn's algorithm
while queue:
u = queue.popleft()
processed_count += 1
# Reduce in-degree of all neighbors
for v in adj[u]:
in_degree[v] -= 1
if in_degree[v] == 0:
queue.append(v)
# If we couldn't process all vertices, cycle exists
return processed_count != n
Complexity
- ⏰ Time complexity:
O(V + E), where V is the number of vertices and E is the number of edges. We process each vertex once and each edge once - 🧺 Space complexity:
O(V + E), for the adjacency list, in-degree array, and BFS queue
Why This Works
- Topological Sort Property: A directed graph can be topologically sorted if and only if it has no cycles
- Kahn's Algorithm: Systematically removes vertices with no incoming edges
- Cycle Detection: If a cycle exists, vertices in the cycle will never have their in-degree reduced to 0, so they won't be processed
- Final Check: If
processedCount < n, some vertices weren't processed, indicating a cycle
Method 3 - Union Find (Not Recommended)
Union Find is not suitable for directed graph cycle detection and should be avoided. The fundamental issue is that Union Find treats all relationships as bidirectional, completely ignoring the directed nature of edges. For a directed edge A → B, Union Find treats it as A ↔ B, which fundamentally misunderstands directed graph semantics.
This leads to both false positives and false negatives. For example, consider edges [A→C, B→C] - Union Find would union A and C, then try to union B and C, incorrectly detecting a "cycle" when there isn't one in the directed graph. The core concept of Union Find is about connecting components bidirectionally, which is fundamentally different from directed graph traversal and cycle detection.