Detect Cycle in Undirected Graph
Problem
Given undirected graph write an algorithm to find out whether graph contains cycle or not.
Examples
Example 1
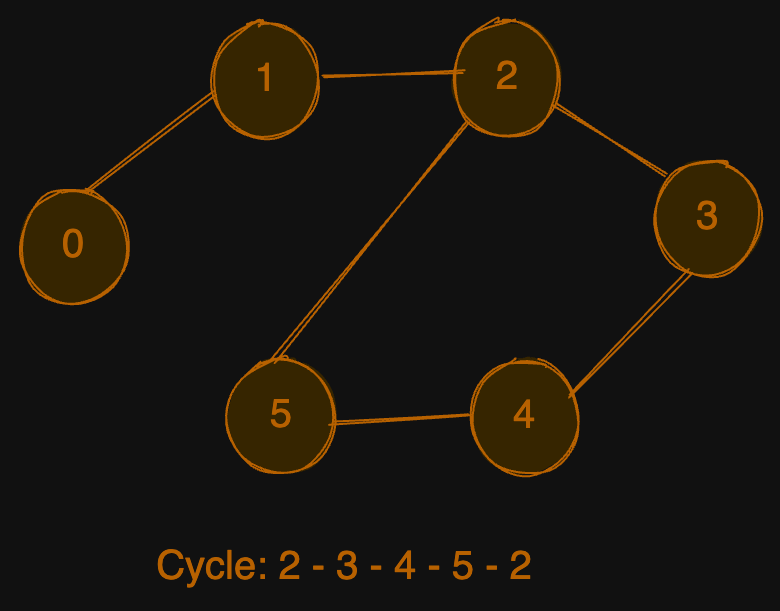
Input: n = 6, edges = [[0,1], [1,2], [2,3], [3,4], [4,5], [5,2]]
Output: true
Explanation: The graph has a cycle: 2 -> 3 -> 4 -> 5 -> 2. Starting from node 2, we can traverse to node 3, then to node 4, then to node 5, and finally back to node 2, forming a cycle.
Example 2
Input: n = 4, edges = [[0,1], [1,2], [2,3]]
Output: false
Explanation: This is a simple path 0-1-2-3 with no cycles. Each node is visited at most once, and there are no back edges.
Example 3
Input: n = 3, edges = [[0,1], [1,2], [0,2]]
Output: true
Explanation: Triangle cycle: 0 -> 1 -> 2 -> 0. All three nodes are connected to each other forming a cycle.
Example 4
Input: n = 1, edges = []
Output: false
Explanation: Single node with no edges cannot form a cycle.
Solution
We have seen [Detect Cycle in Directed Graph](detect-cycle-in-directed-graph). Now we will solve it for undirected graph. This problem can be solved in multiple ways, like topological sort, DFS, disjoint sets, etc.
Method 1 - DFS and Parent
DFS for a connected graph produces a tree. There is a cycle in a graph only if there is a back edge present in the graph. We have seen Types of Edges in Graph.
A back edge is an edge that is joining a node to itself (self-loop) or one of its ancestor in the tree produced by DFS. To find the back edge to any of its ancestors keep a visited array and if there is a back edge to any visited node then there is a loop and return true.
Algorithm
- Do DFS from every vertex (please read DFS for more details)
- During DFS, for any current vertex 'u' (currently visiting vertex) if there is an adjacent vertex 'v' that is already visited and 'v' is not a direct parent of 'u' then there is a cycle in the graph
- Why we ignore parent:
- Let's assume vertices
uandvwith edge between them: u—-v - When we do DFS from
uand reachv, then fromvwe seeuas adjacent and already visited - But this doesn't indicate a cycle since
uis the parent ofv - That's why we ignore the visited vertex if it is the parent of the current vertex
- Let's assume vertices
Code
C++
class Solution {
public:
bool hasCycle(int n, vector<vector<int>>& edges) {
// Build adjacency list
vector<vector<int>> adj(n);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
}
vector<bool> visited(n, false);
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, -1, adj, visited)) {
return true;
}
}
}
return false;
}
private:
bool dfs(int u, int parent, vector<vector<int>>& adj, vector<bool>& visited) {
visited[u] = true;
// Visit all adjacent vertices
for (int v : adj[u]) {
if (!visited[v]) {
// If not visited, recurse
if (dfs(v, u, adj, visited)) {
return true;
}
} else if (v != parent) {
// If visited and not parent, cycle found
return true;
}
}
return false;
}
};
Java
class Solution {
public boolean hasCycle(int n, int[][] edges) {
// Build adjacency list
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
adj.get(edge[1]).add(edge[0]);
}
boolean[] visited = new boolean[n];
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (dfs(i, -1, adj, visited)) {
return true;
}
}
}
return false;
}
private boolean dfs(int u, int parent, List<List<Integer>> adj, boolean[] visited) {
visited[u] = true;
// Visit all adjacent vertices
for (int v : adj.get(u)) {
if (!visited[v]) {
// If not visited, recurse
if (dfs(v, u, adj, visited)) {
return true;
}
} else if (v != parent) {
// If visited and not parent, cycle found
return true;
}
}
return false;
}
}
Python
class Solution:
def has_cycle(self, n: int, edges: List[List[int]]) -> bool:
# Build adjacency list
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
visited = [False] * n
# Check each component
for i in range(n):
if not visited[i]:
if self._dfs(i, -1, adj, visited):
return True
return False
def _dfs(self, u: int, parent: int, adj: List[List[int]], visited: List[bool]) -> bool:
visited[u] = True
# Visit all adjacent vertices
for v in adj[u]:
if not visited[v]:
# If not visited, recurse
if self._dfs(v, u, adj, visited):
return True
elif v != parent:
# If visited and not parent, cycle found
return True
return False
Complexity
- ⏰ Time complexity:
O(V + E), where V is the number of vertices and E is the number of edges. We visit each vertex once and traverse each edge twice (once from each endpoint) - 🧺 Space complexity:
O(V + E), for the adjacency list representation and the recursion stack which can go up to O(V) in the worst case
Method 2 - BFS and Parent Tracking
Similar to DFS approach, we can use BFS to detect cycles in an undirected graph. The key insight is the same: if we encounter a visited vertex that is not the direct parent of the current vertex, then we have found a cycle.
Algorithm
- Use BFS from every unvisited vertex
- For each vertex, keep track of its parent in the BFS tree
- During BFS, if we encounter an adjacent vertex that is already visited and is not the parent of the current vertex, then there is a cycle
- Use a queue to store pairs of (vertex, parent) for BFS traversal
Code
C++
class Solution {
public:
bool hasCycle(int n, vector<vector<int>>& edges) {
// Build adjacency list
vector<vector<int>> adj(n);
for (auto& edge : edges) {
adj[edge[0]].push_back(edge[1]);
adj[edge[1]].push_back(edge[0]);
}
vector<bool> visited(n, false);
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (bfs(i, adj, visited)) {
return true;
}
}
}
return false;
}
private:
bool bfs(int start, vector<vector<int>>& adj, vector<bool>& visited) {
queue<pair<int, int>> q; // {vertex, parent}
q.push({start, -1});
visited[start] = true;
while (!q.empty()) {
auto [u, parent] = q.front();
q.pop();
// Visit all adjacent vertices
for (int v : adj[u]) {
if (!visited[v]) {
// If not visited, add to queue
visited[v] = true;
q.push({v, u});
} else if (v != parent) {
// If visited and not parent, cycle found
return true;
}
}
}
return false;
}
};
Java
class Solution {
public boolean hasCycle(int n, int[][] edges) {
// Build adjacency list
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
adj.get(edge[1]).add(edge[0]);
}
boolean[] visited = new boolean[n];
// Check each component
for (int i = 0; i < n; i++) {
if (!visited[i]) {
if (bfs(i, adj, visited)) {
return true;
}
}
}
return false;
}
private boolean bfs(int start, List<List<Integer>> adj, boolean[] visited) {
Queue<int[]> queue = new LinkedList<>(); // {vertex, parent}
queue.offer(new int[]{start, -1});
visited[start] = true;
while (!queue.isEmpty()) {
int[] current = queue.poll();
int u = current[0];
int parent = current[1];
// Visit all adjacent vertices
for (int v : adj.get(u)) {
if (!visited[v]) {
// If not visited, add to queue
visited[v] = true;
queue.offer(new int[]{v, u});
} else if (v != parent) {
// If visited and not parent, cycle found
return true;
}
}
}
return false;
}
}
Python
from collections import deque
from typing import List
class Solution:
def has_cycle(self, n: int, edges: List[List[int]]) -> bool:
# Build adjacency list
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
visited = [False] * n
# Check each component
for i in range(n):
if not visited[i]:
if self._bfs(i, adj, visited):
return True
return False
def _bfs(self, start: int, adj: List[List[int]], visited: List[bool]) -> bool:
queue = deque([(start, -1)]) # (vertex, parent)
visited[start] = True
while queue:
u, parent = queue.popleft()
# Visit all adjacent vertices
for v in adj[u]:
if not visited[v]:
# If not visited, add to queue
visited[v] = True
queue.append((v, u))
elif v != parent:
# If visited and not parent, cycle found
return True
return False
Complexity
- ⏰ Time complexity:
O(V + E), where V is the number of vertices and E is the number of edges. We visit each vertex once and traverse each edge twice - 🧺 Space complexity:
O(V + E), for the adjacency list representation and the BFS queue which can hold up to O(V) elements
Method 3 - Union Find (Disjoint Set)
Union Find (also known as Disjoint Set Union) is another efficient approach to detect cycles in undirected graphs. The key insight is that if two vertices of an edge are already in the same connected component (same set), then adding this edge will create a cycle.
Algorithm
- Initialize each vertex as its own parent (each vertex is in its own set)
- For each edge (u, v):
- Find the root/representative of vertex u
- Find the root/representative of vertex v
- If both vertices have the same root, they are already connected, so adding this edge creates a cycle
- Otherwise, union the two sets by making one root the parent of the other
Example Walkthrough
Let's trace through Example 1: n = 6, edges = [[0,1], [1,2], [2,3], [3,4], [4,5], [5,2]]
Initial state: Each vertex is its own parent
parent: [0, 1, 2, 3, 4, 5]
Edge [0,1]: Different sets, union them
parent: [1, 1, 2, 3, 4, 5] // 0 joins 1's set
Edge [1,2]: Different sets, union them
parent: [1, 2, 2, 3, 4, 5] // 1 joins 2's set
Edge [2,3]: Different sets, union them
parent: [1, 2, 3, 3, 4, 5] // 2 joins 3's set
Edge [3,4]: Different sets, union them
parent: [1, 2, 3, 4, 4, 5] // 3 joins 4's set
Edge [4,5]: Different sets, union them
parent: [1, 2, 3, 4, 5, 5] // 4 joins 5's set
Edge [5,2]: Check if 5 and 2 are in same set
- Root of 5: 5
- Root of 2: 2 → 3 → 4 → 5 (following parent chain)
- Both have root 5, so they're already connected! Cycle detected!
Code
C++
class UnionFind {
private:
vector<int> parent;
vector<int> rank;
public:
UnionFind(int n) {
parent.resize(n);
rank.resize(n, 0);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]); // Path compression
}
return parent[x];
}
bool unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return false; // Already in same set, cycle detected
}
// Union by rank
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
return true;
}
};
class Solution {
public:
bool hasCycle(int n, vector<vector<int>>& edges) {
UnionFind uf(n);
for (auto& edge : edges) {
if (!uf.unite(edge[0], edge[1])) {
return true; // Cycle detected
}
}
return false;
}
};
Java
class UnionFind {
private int[] parent;
private int[] rank;
public UnionFind(int n) {
parent = new int[n];
rank = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
rank[i] = 0;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]); // Path compression
}
return parent[x];
}
public boolean unite(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return false; // Already in same set, cycle detected
}
// Union by rank
if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
return true;
}
}
class Solution {
public boolean hasCycle(int n, int[][] edges) {
UnionFind uf = new UnionFind(n);
for (int[] edge : edges) {
if (!uf.unite(edge[0], edge[1])) {
return true; // Cycle detected
}
}
return false;
}
}
Python
class UnionFind:
def __init__(self, n: int):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, x: int) -> int:
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # Path compression
return self.parent[x]
def unite(self, x: int, y: int) -> bool:
root_x = self.find(x)
root_y = self.find(y)
if root_x == root_y:
return False # Already in same set, cycle detected
# Union by rank
if self.rank[root_x] < self.rank[root_y]:
self.parent[root_x] = root_y
elif self.rank[root_x] > self.rank[root_y]:
self.parent[root_y] = root_x
else:
self.parent[root_y] = root_x
self.rank[root_x] += 1
return True
class Solution:
def has_cycle(self, n: int, edges: List[List[int]]) -> bool:
uf = UnionFind(n)
for u, v in edges:
if not uf.unite(u, v):
return True # Cycle detected
return False
Complexity
- ⏰ Time complexity:
O(E × α(V)), where E is the number of edges, V is the number of vertices, and α is the inverse Ackermann function. With path compression and union by rank, α(V) is effectively constant for all practical purposes, making it nearlyO(E) - 🧺 Space complexity:
O(V), for the parent and rank arrays in the Union Find data structure
Key Optimizations
- Path Compression: During find operation, make every node point directly to the root
- Union by Rank: Always attach the shorter tree under the root of the taller tree to keep trees flat