Detect Cycles in 2D Grid
Problem
Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.
A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.
Return true if any cycle of the same value exists in grid, otherwise, return false.
Examples
Example 1
**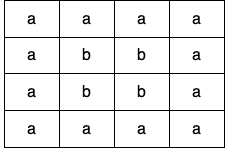**
Input: grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
Output: true
Explanation: There are two valid cycles shown in different colors in the image below:
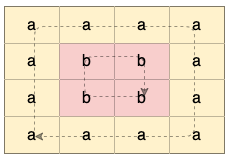
Example 2
**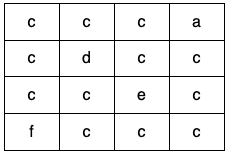**
Input: grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
Output: true
Explanation: There is only one valid cycle highlighted in the image below:
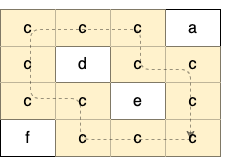
Example 3
****
Input: grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
Output: false
Constraints
m == grid.lengthn == grid[i].length1 <= m, n <= 500gridconsists only of lowercase English letters.
Solution
Method 1 – DFS with Parent Tracking
Intuition
A cycle exists if we can revisit a cell (with the same character) that is not the immediate parent in the DFS path. We use DFS to traverse the grid, marking visited cells, and track the previous cell to avoid trivial backtracking.
Approach
- For each unvisited cell, start a DFS.
- In DFS, for each direction (up, down, left, right):
- Skip the cell we just came from (the parent).
- If the next cell is in bounds, has the same character, and is visited, a cycle is found.
- If not visited, continue DFS.
- If any DFS finds a cycle, return true.
- If no cycles are found after all traversals, return false.
Code
C++
class Solution {
public:
int m, n;
vector<vector<bool>> vis;
bool dfs(vector<vector<char>>& grid, int x, int y, int px, int py, char ch) {
vis[x][y] = true;
int dirs[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
for (auto& d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx == px && ny == py) continue;
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == ch) {
if (vis[nx][ny]) return true;
if (dfs(grid, nx, ny, x, y, ch)) return true;
}
}
return false;
}
bool containsCycle(vector<vector<char>>& grid) {
m = grid.size(); n = grid[0].size();
vis = vector<vector<bool>>(m, vector<bool>(n, false));
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (!vis[i][j]) {
if (dfs(grid, i, j, -1, -1, grid[i][j])) return true;
}
}
}
return false;
}
};
Go
func containsCycle(grid [][]byte) bool {
m, n := len(grid), len(grid[0])
vis := make([][]bool, m)
for i := range vis {
vis[i] = make([]bool, n)
}
var dfs func(x, y, px, py int, ch byte) bool
dirs := [][2]int{{0,1},{1,0},{0,-1},{-1,0}}
dfs = func(x, y, px, py int, ch byte) bool {
vis[x][y] = true
for _, d := range dirs {
nx, ny := x+d[0], y+d[1]
if nx == px && ny == py {
continue
}
if nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == ch {
if vis[nx][ny] {
return true
}
if dfs(nx, ny, x, y, ch) {
return true
}
}
}
return false
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if !vis[i][j] {
if dfs(i, j, -1, -1, grid[i][j]) {
return true
}
}
}
}
return false
}
Java
class Solution {
int m, n;
boolean[][] vis;
int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
boolean dfs(char[][] grid, int x, int y, int px, int py, char ch) {
vis[x][y] = true;
for (int[] d : dirs) {
int nx = x + d[0], ny = y + d[1];
if (nx == px && ny == py) continue;
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == ch) {
if (vis[nx][ny]) return true;
if (dfs(grid, nx, ny, x, y, ch)) return true;
}
}
return false;
}
public boolean containsCycle(char[][] grid) {
m = grid.length; n = grid[0].length;
vis = new boolean[m][n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (!vis[i][j]) {
if (dfs(grid, i, j, -1, -1, grid[i][j])) return true;
}
}
}
return false;
}
}
Kotlin
class Solution {
private val dirs = arrayOf(intArrayOf(0,1), intArrayOf(1,0), intArrayOf(0,-1), intArrayOf(-1,0))
fun containsCycle(grid: Array<CharArray>): Boolean {
val m = grid.size
val n = grid[0].size
val vis = Array(m) { BooleanArray(n) }
fun dfs(x: Int, y: Int, px: Int, py: Int, ch: Char): Boolean {
vis[x][y] = true
for ((dx, dy) in dirs) {
val nx = x + dx
val ny = y + dy
if (nx == px && ny == py) continue
if (nx in 0 until m && ny in 0 until n && grid[nx][ny] == ch) {
if (vis[nx][ny]) return true
if (dfs(nx, ny, x, y, ch)) return true
}
}
return false
}
for (i in 0 until m) {
for (j in 0 until n) {
if (!vis[i][j]) {
if (dfs(i, j, -1, -1, grid[i][j])) return true
}
}
}
return false
}
}
Python
class Solution:
def containsCycle(self, grid: list[list[str]]) -> bool:
m, n = len(grid), len(grid[0])
vis = [[False]*n for _ in range(m)]
def dfs(x: int, y: int, px: int, py: int, ch: str) -> bool:
vis[x][y] = True
for dx, dy in ((0,1),(1,0),(0,-1),(-1,0)):
nx, ny = x+dx, y+dy
if nx == px and ny == py:
continue
if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == ch:
if vis[nx][ny]:
return True
if dfs(nx, ny, x, y, ch):
return True
return False
for i in range(m):
for j in range(n):
if not vis[i][j]:
if dfs(i, j, -1, -1, grid[i][j]):
return True
return False
Rust
impl Solution {
pub fn contains_cycle(grid: Vec<Vec<char>>) -> bool {
let m = grid.len();
let n = grid[0].len();
let mut vis = vec![vec![false; n]; m];
fn dfs(grid: &Vec<Vec<char>>, vis: &mut Vec<Vec<bool>>, x: usize, y: usize, px: isize, py: isize, ch: char) -> bool {
vis[x][y] = true;
let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
for (dx, dy) in dirs.iter() {
let nx = x as isize + dx;
let ny = y as isize + dy;
if nx == px && ny == py { continue; }
if nx >= 0 && nx < vis.len() as isize && ny >= 0 && ny < vis[0].len() as isize {
let nxu = nx as usize;
let nyu = ny as usize;
if grid[nxu][nyu] == ch {
if vis[nxu][nyu] { return true; }
if dfs(grid, vis, nxu, nyu, x as isize, y as isize, ch) { return true; }
}
}
}
false
}
for i in 0..m {
for j in 0..n {
if !vis[i][j] {
if dfs(&grid, &mut vis, i, j, -1, -1, grid[i][j]) {
return true;
}
}
}
}
false
}
}
TypeScript
class Solution {
containsCycle(grid: string[][]): boolean {
const m = grid.length, n = grid[0].length;
const vis: boolean[][] = Array.from({length: m}, () => Array(n).fill(false));
const dirs = [[0,1],[1,0],[0,-1],[-1,0]];
const dfs = (x: number, y: number, px: number, py: number, ch: string): boolean => {
vis[x][y] = true;
for (const [dx, dy] of dirs) {
const nx = x + dx, ny = y + dy;
if (nx === px && ny === py) continue;
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] === ch) {
if (vis[nx][ny]) return true;
if (dfs(nx, ny, x, y, ch)) return true;
}
}
return false;
};
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (!vis[i][j]) {
if (dfs(i, j, -1, -1, grid[i][j])) return true;
}
}
}
return false;
}
}
Complexity
- ⏰ Time complexity:
O(m * n), since each cell is visited at most once in DFS. - 🧺 Space complexity:
O(m * n), for the visited matrix and recursion stack.