Determine Whether Matrix Can Be Obtained By Rotation

Problem

Given two n x n binary matrices mat and target, return true if it is possible to makemat equal totarget _byrotating _mat _in90-degree increments , or _false otherwise.

Examples

Example 1

![](https://assets.leetcode.com/uploads/2021/05/20/grid3.png)

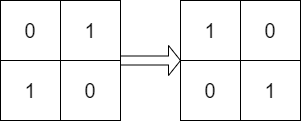
Input: mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise to make mat equal target.

Example 2

![](https://assets.leetcode.com/uploads/2021/05/20/grid4.png)

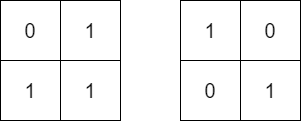
Input: mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
Output: false
Explanation: It is impossible to make mat equal to target by rotating mat.

Example 3

![](https://assets.leetcode.com/uploads/2021/05/26/grid4.png)

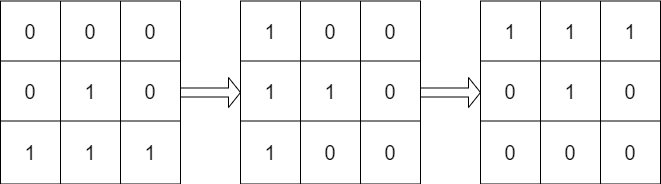
Input: mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
Output: true
Explanation: We can rotate mat 90 degrees clockwise two times to make mat equal target.

Constraints

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] and target[i][j] are either 0 or 1.

Solution

Method 1 – Simulate All Rotations

Intuition

A matrix can be rotated 0, 90, 180, or 270 degrees. For each rotation, check if the rotated matrix matches the target. If any rotation matches, return true.

Approach

1. For up to 4 times, check if mat equals target.
2. If not, rotate mat 90 degrees clockwise.
3. If any rotation matches, return true. If none match, return false.

Code

C++

class Solution {
public:
    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        int n = mat.size();
        for (int r = 0; r < 4; ++r) {
            if (mat == target) return true;
            vector<vector<int>> rot(n, vector<int>(n));
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    rot[j][n-1-i] = mat[i][j];
            mat = rot;
        }
        return false;
    }
};

Go

func findRotation(mat [][]int, target [][]int) bool {
    n := len(mat)
    for r := 0; r < 4; r++ {
        ok := true
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                if mat[i][j] != target[i][j] {
                    ok = false
                    break
                }
            }
            if !ok { break }
        }
        if ok { return true }
        rot := make([][]int, n)
        for i := range rot {
            rot[i] = make([]int, n)
        }
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                rot[j][n-1-i] = mat[i][j]
            }
        }
        mat = rot
    }
    return false
}

Java

class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int n = mat.length;
        for (int r = 0; r < 4; ++r) {
            boolean ok = true;
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    if (mat[i][j] != target[i][j]) ok = false;
            if (ok) return true;
            int[][] rot = new int[n][n];
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    rot[j][n-1-i] = mat[i][j];
            mat = rot;
        }
        return false;
    }
}

Kotlin

class Solution {
    fun findRotation(mat: Array<IntArray>, target: Array<IntArray>): Boolean {
        val n = mat.size
        var m = mat.map { it.copyOf() }.toTypedArray()
        repeat(4) {
            if ((0 until n).all { i -> (0 until n).all { j -> m[i][j] == target[i][j] } }) return true
            val rot = Array(n) { IntArray(n) }
            for (i in 0 until n)
                for (j in 0 until n)
                    rot[j][n-1-i] = m[i][j]
            m = rot
        }
        return false
    }
}

Python

class Solution:
    def findRotation(self, mat: list[list[int]], target: list[list[int]]) -> bool:
        n = len(mat)
        m = [row[:] for row in mat]
        for _ in range(4):
            if m == target:
                return True
            m = [[m[n-j-1][i] for j in range(n)] for i in range(n)]
        return False

Rust

impl Solution {
    pub fn find_rotation(mut mat: Vec<Vec<i32>>, target: Vec<Vec<i32>>) -> bool {
        let n = mat.len();
        for _ in 0..4 {
            if mat == target { return true; }
            let mut rot = vec![vec![0; n]; n];
            for i in 0..n {
                for j in 0..n {
                    rot[j][n-1-i] = mat[i][j];
                }
            }
            mat = rot;
        }
        false
    }
}

TypeScript

class Solution {
    findRotation(mat: number[][], target: number[][]): boolean {
        const n = mat.length;
        let m = mat.map(row => row.slice());
        for (let r = 0; r < 4; ++r) {
            let ok = true;
            for (let i = 0; i < n; ++i)
                for (let j = 0; j < n; ++j)
                    if (m[i][j] !== target[i][j]) ok = false;
            if (ok) return true;
            const rot = Array.from({length: n}, () => Array(n).fill(0));
            for (let i = 0; i < n; ++i)
                for (let j = 0; j < n; ++j)
                    rot[j][n-1-i] = m[i][j];
            m = rot;
        }
        return false;
    }
}

Complexity

• ⏰ Time complexity: O(n^2), for each of 4 rotations, we compare and rotate the matrix.
• 🧺 Space complexity: O(n^2), for storing the rotated matrix.