Problem

Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

Examples

Example 1:

1
2

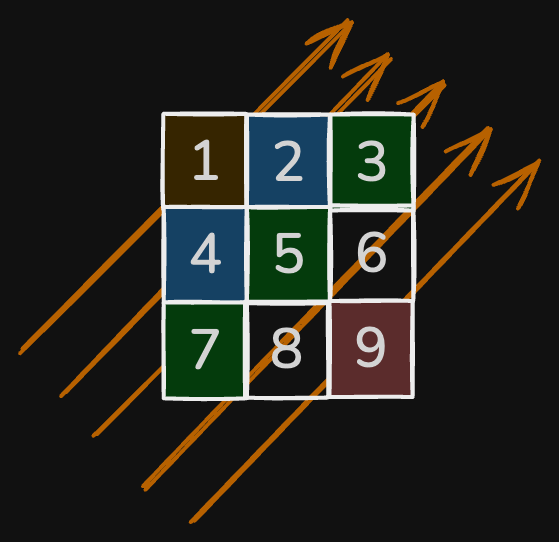
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

1
2

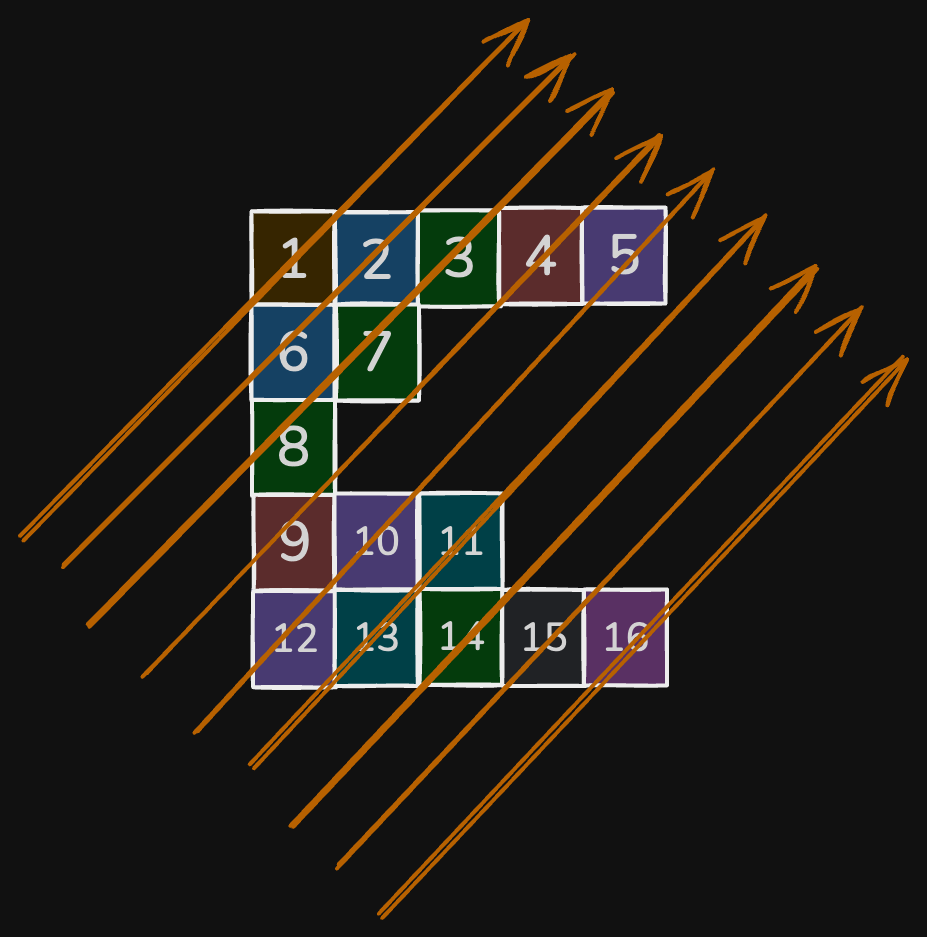
Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

Solution

Method 1 - Using hashmap

Here is the approach:

  1. Using a HashMap to Group Elements by Diagonals:
    • Traverse the matrix and use a hashmap to collect elements that belong to the same diagonal.
    • The key for each diagonal in the hashmap is the sum of the row and column indices.
  2. Extract Elements from the HashMap:
    • Read the diagonals from the hashmap in increasing order of their keys and collect elements.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

public class Solution {
    public int[] findDiagonalOrder(List<List<Integer>> nums) {
        Map<Integer, List<Integer>> diagonals = new HashMap<>();
        int maxKey = 0;
        int size = 0;

        // Traverse the matrix and populate the diagonals hashmap
        for (int i = 0; i < nums.size(); i++) {
            for (int j = 0; j < nums.get(i).size(); j++) {
                diagonals.putIfAbsent(i + j, new ArrayList<>());
                diagonals.get(i + j).add(nums.get(i).get(j));
                maxKey = Math.max(maxKey, i + j);
                size++;
            }
        }

        // Read the diagonals from the hashmap in increasing order of their keys
        int[] result = new int[size];
        int index = 0;
        for (int key = 0; key <= maxKey; key++) {
            if (diagonals.containsKey(key)) {
                for (int value : diagonals.get(key)) {
                    result[index++] = value;
                }
            }
        }

        return result;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def findDiagonalOrder(self, nums: List[List[int]]) -> List[int]:
        diagonals: Dict[int, List[int]] = defaultdict(list)
        max_key = 0
        total_elements = 0

        # Traverse the matrix and populate the diagonals defaultdict
        for i in range(len(nums)):
            for j in range(len(nums[i])):
                diagonals[i + j].append(nums[i][j])
                max_key = max(max_key, i + j)
                total_elements += 1

        # Read the diagonals from the defaultdict in increasing order of their keys
        result = []
        for key in range(max_key + 1):
            if key in diagonals:
                result.extend(diagonals[key])

        return result

Complexity

  • Time: O(m * n), where m is the number of rows and n is the number of columns. This is because we visit each element exactly once.
  • Space: O(m * n), for storing the elements in the hashmap and the result list.