Problem

Given a binary tree, find the diameter of it.

Definition

Diameter of tree is defined as a longest path or route between any two nodes in a tree. The path may or may not for through the root.

Example

Example 1:

1
2
3
4
5
6
7
8
9

	 1
   /   \
  2     3
 /  \   
4    5

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

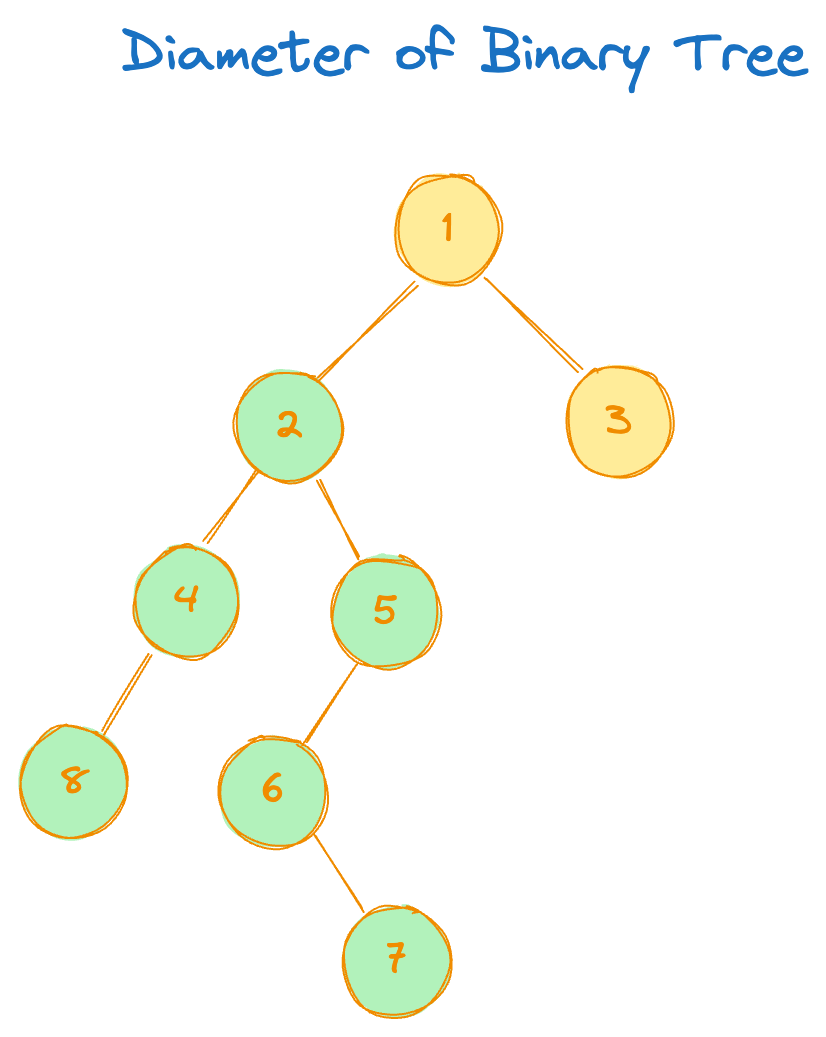
Example 2:

1
2
3

Input:
root = [1,2,3,4,5,null, null, 8, null, 6, null, null, null, null, 7]
Output: 5

Note that diameter here doesn’t include root.

Solution

Method 1 - Naive Approach

The diameter of a binary tree refers to the length of the longest path between any two leaves. This path can:

  • Reside entirely within the left subtree.
  • Reside entirely within the right subtree.
  • Pass through the root node, connecting leaves from both subtrees.

Algorithm

A straightforward approach involves recursively calculating the diameter:

  1. Find the height of both the left and right subtrees.
  2. Compute the diameter of the left subtree.
  3. Compute the diameter of the right subtree.
  4. Calculate the longest path that passes through the root by adding 1 (for the root itself) to the sum of the left and right subtree heights.
  5. The diameter is the maximum of these three values.

Read more - Height of Binary Tree.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

public int diameterOfBinaryTree(TreeNode root) {
	if (root == null) {
		return 0;
	}

	int leftHeight = maxDepth(root.left);
	int rightHeight = maxDepth(root.right);

	int leftDiameter = diameter(root.left);
	int rightDiameter = diameter(root.right);

	return max(leftDiameter, rightDiameter, leftHeight + rightHeight + 1);
}

public int maxDepth(TreeNode root) {
	if (root != null) {
		return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
	}
	return 0;
}

private int max(int a, int b, int c) {
	return Math.max(a, Math.max(b, c));
}

Complexity

  • Time complexity - O(N^2). However, this approach suffers from redundancy as it calculates the height of each node multiple times, leading to a time complexity of O(N^2).

Method 2 - Return Height and Diameter in Same Iteration

To optimize the calculation, we can modify the function to compute the height and diameter simultaneously.

Algorithm

  • During the recursive traversal, calculate both the height and the maximum diameter encountered so far for each subtree.
  • The height returned by a subtree function represents the maximum depth from that subtree’s root to a leaf node (including the root).
  • The diameter returned by a subtree function represents the maximum diameter found within that subtree or the longest path passing through the subtree’s root.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

public int diameterOfBinaryTree(TreeNode root) {
	if(root == null){
		return 0;
	}
	return getDiameter(root)[0] - 1;
}

private int[] diameterOfBinaryTree(TreeNode root) {
	int dAndH[] = { 0, 0 }; // first diameter, second height

	int[] leftResult = diameter(root.left);
	int[] rightResult = diameter(root.right);

	int height = Math.max(leftResult[1], rightResult[1]) + 1;
	
	int leftDiameter = leftResult[0];
	int rightDiameter = rightResult[0];
	int rootDiameter = leftResult[1] + rightResult[1] + 1;
	
	int finalDiameter = max(leftDiameter, rightDiameter,
		rootDiameter);

	dAndH[0] = height;
	dAndH[1] = finalDiameter;
	
	return DandH;
}
 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

public int diameterOfBinaryTree(TreeNode root) {
	if(root == null){
		return 0;
	}
	return diameter(root, new int[1]{});
}

private int diameter(TreeNode root, int[] height) {
	if (root == null) {
		height[0] = 0;
		return 0;
	}

	int[] leftHeight = { 0 }, rightHeight = { 0 };
	int leftDiam = diameter(root.left, leftHeight);
	int rightDiam = diameter(root.right, rightHeight);

	height[0] = Math.max(leftHeight[0], rightHeight[0]) + 1;

	return max(leftDiam, rightDiam, leftHeight[0] + rightHeight[0] + 1);
}

Complexity

  • Time Complexity - O(n)