Difference Between Maximum and Minimum Price Sum

Problem

There exists an undirected and initially unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Each node has an associated price. You are given an integer array price, where price[i] is the price of the ith node.

The price sum of a given path is the sum of the prices of all nodes lying on that path.

The tree can be rooted at any node root of your choice. The incurred cost after choosing root is the difference between the maximum and minimum price sum amongst all paths starting at root.

Return themaximum possible cost amongst all possible root choices.

Examples

Example 1

1
2
3
4
5
6
7
8
9



![](https://assets.leetcode.com/uploads/2022/12/01/example14.png)

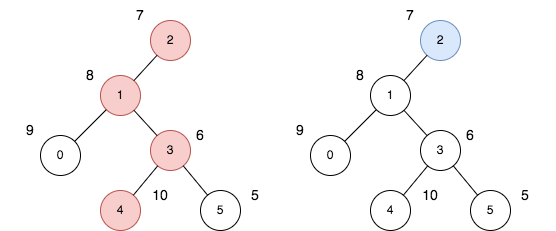
Input: n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
Output: 24
Explanation: The diagram above denotes the tree after rooting it at node 2. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes [2,1,3,4]: the prices are [7,8,6,10], and the sum of the prices is 31.
- The second path contains the node [2] with the price [7].
The difference between the maximum and minimum price sum is 24. It can be proved that 24 is the maximum cost.

Example 2

1
2
3
4
5
6
7
8
9



![](https://assets.leetcode.com/uploads/2022/11/24/p1_example2.png)

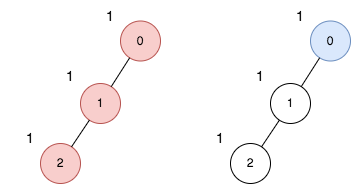
Input: n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
Output: 2
Explanation: The diagram above denotes the tree after rooting it at node 0. The first part (colored in red) shows the path with the maximum price sum. The second part (colored in blue) shows the path with the minimum price sum.
- The first path contains nodes [0,1,2]: the prices are [1,1,1], and the sum of the prices is 3.
- The second path contains node [0] with a price [1].
The difference between the maximum and minimum price sum is 2. It can be proved that 2 is the maximum cost.

Constraints

1 <= n <= 10^5
edges.length == n - 1
0 <= ai, bi <= n - 1
edges represents a valid tree.
price.length == n
1 <= price[i] <= 10^5

Solution

Method 1 – Rerooting DP (Dynamic Programming on Trees)

Intuition

For each possible root, the cost is the difference between the maximum and minimum price sum of all paths starting at that root. The maximum path sum is the largest sum from the root to any leaf, and the minimum is the smallest such sum. We can use dynamic programming to compute these values efficiently for all possible roots using a rerooting technique.

Approach

Build the tree as an adjacency list.
For each node, compute the maximum and minimum path sum from that node to any leaf using DFS.
Use rerooting DP to efficiently compute the answer for all possible roots:
- For each node, when rerooting to a child, update the max/min path sum accordingly.
- Track the best (maximum) difference for all roots.
Return the maximum difference found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58


class Solution {
public:
    vector<vector<int>> g;
    vector<int> price;
    int ans = 0;
    int dfs(int u, int p, int &mx, int &mn) {
        mx = mn = price[u];
        for (int v : g[u]) {
            if (v == p) continue;
            int cmx, cmn;
            dfs(v, u, cmx, cmn);
            mx = max(mx, price[u] + cmx);
            mn = min(mn, price[u] + cmn);
        }
        return 0;
    }
    void reroot(int u, int p, int upmx, int upmn) {
        int mx = price[u], mn = price[u];
        vector<pair<int,int>> child;
        for (int v : g[u]) {
            if (v == p) continue;
            int cmx, cmn;
            dfs(v, u, cmx, cmn);
            child.push_back({cmx, cmn});
            mx = max(mx, price[u] + cmx);
            mn = min(mn, price[u] + cmn);
        }
        mx = max(mx, price[u] + upmx);
        mn = min(mn, price[u] + upmn);
        ans = max(ans, mx - mn);
        int idx = 0;
        for (int v : g[u]) {
            if (v == p) continue;
            int nmx = price[u], nmn = price[u];
            for (int j = 0; j < child.size(); ++j) {
                if (j == idx) continue;
                nmx = max(nmx, price[u] + child[j].first);
                nmn = min(nmn, price[u] + child[j].second);
            }
            nmx = max(nmx, price[u] + upmx);
            nmn = min(nmn, price[u] + upmn);
            reroot(v, u, nmx - price[v], nmn - price[v]);
            idx++;
        }
    }
    int maxOutput(int n, vector<vector<int>>& edges, vector<int>& price_) {
        g.assign(n, {});
        price = price_;
        for (auto &e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        int mx, mn;
        dfs(0, -1, mx, mn);
        reroot(0, -1, 0, 0);
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


func maxOutput(n int, edges [][]int, price []int) int {
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    var ans int
    var dfs func(u, p int) (int, int)
    dfs = func(u, p int) (int, int) {
        mx, mn := price[u], price[u]
        for _, v := range g[u] {
            if v == p { continue }
            cmx, cmn := dfs(v, u)
            if mx < price[u]+cmx { mx = price[u]+cmx }
            if mn > price[u]+cmn { mn = price[u]+cmn }
        }
        return mx, mn
    }
    var reroot func(u, p, upmx, upmn int)
    reroot = func(u, p, upmx, upmn int) {
        mx, mn := price[u], price[u]
        child := [][2]int{}
        for _, v := range g[u] {
            if v == p { continue }
            cmx, cmn := dfs(v, u)
            child = append(child, [2]int{cmx, cmn})
            if mx < price[u]+cmx { mx = price[u]+cmx }
            if mn > price[u]+cmn { mn = price[u]+cmn }
        }
        if mx < price[u]+upmx { mx = price[u]+upmx }
        if mn > price[u]+upmn { mn = price[u]+upmn }
        if ans < mx-mn { ans = mx-mn }
        idx := 0
        for _, v := range g[u] {
            if v == p { continue }
            nmx, nmn := price[u], price[u]
            for j, c := range child {
                if j == idx { continue }
                if nmx < price[u]+c[0] { nmx = price[u]+c[0] }
                if nmn > price[u]+c[1] { nmn = price[u]+c[1] }
            }
            if nmx < price[u]+upmx { nmx = price[u]+upmx }
            if nmn > price[u]+upmn { nmn = price[u]+upmn }
            reroot(v, u, nmx-price[v], nmn-price[v])
            idx++
        }
    }
    dfs(0, -1)
    reroot(0, -1, 0, 0)
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55


class Solution {
    List<List<Integer>> g;
    int[] price;
    int ans = 0;
    int[] dfs(int u, int p) {
        int mx = price[u], mn = price[u];
        for (int v : g.get(u)) {
            if (v == p) continue;
            int[] t = dfs(v, u);
            mx = Math.max(mx, price[u] + t[0]);
            mn = Math.min(mn, price[u] + t[1]);
        }
        return new int[]{mx, mn};
    }
    void reroot(int u, int p, int upmx, int upmn) {
        int mx = price[u], mn = price[u];
        List<int[]> child = new ArrayList<>();
        for (int v : g.get(u)) {
            if (v == p) continue;
            int[] t = dfs(v, u);
            child.add(t);
            mx = Math.max(mx, price[u] + t[0]);
            mn = Math.min(mn, price[u] + t[1]);
        }
        mx = Math.max(mx, price[u] + upmx);
        mn = Math.min(mn, price[u] + upmn);
        ans = Math.max(ans, mx - mn);
        int idx = 0;
        for (int v : g.get(u)) {
            if (v == p) continue;
            int nmx = price[u], nmn = price[u];
            for (int j = 0; j < child.size(); ++j) {
                if (j == idx) continue;
                nmx = Math.max(nmx, price[u] + child.get(j)[0]);
                nmn = Math.min(nmn, price[u] + child.get(j)[1]);
            }
            nmx = Math.max(nmx, price[u] + upmx);
            nmn = Math.min(nmn, price[u] + upmn);
            reroot(v, u, nmx - price[v], nmn - price[v]);
            idx++;
        }
    }
    public int maxOutput(int n, int[][] edges, int[] price) {
        g = new ArrayList<>();
        this.price = price;
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        dfs(0, -1);
        reroot(0, -1, 0, 0);
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


class Solution {
    lateinit var g: Array<MutableList<Int>>
    lateinit var price: IntArray
    var ans = 0
    fun dfs(u: Int, p: Int): Pair<Int, Int> {
        var mx = price[u]
        var mn = price[u]
        for (v in g[u]) {
            if (v == p) continue
            val (cmx, cmn) = dfs(v, u)
            mx = maxOf(mx, price[u] + cmx)
            mn = minOf(mn, price[u] + cmn)
        }
        return mx to mn
    }
    fun reroot(u: Int, p: Int, upmx: Int, upmn: Int) {
        var mx = price[u]
        var mn = price[u]
        val child = mutableListOf<Pair<Int, Int>>()
        for (v in g[u]) {
            if (v == p) continue
            val (cmx, cmn) = dfs(v, u)
            child.add(cmx to cmn)
            mx = maxOf(mx, price[u] + cmx)
            mn = minOf(mn, price[u] + cmn)
        }
        mx = maxOf(mx, price[u] + upmx)
        mn = minOf(mn, price[u] + upmn)
        ans = maxOf(ans, mx - mn)
        var idx = 0
        for (v in g[u]) {
            if (v == p) continue
            var nmx = price[u]
            var nmn = price[u]
            for (j in child.indices) {
                if (j == idx) continue
                nmx = maxOf(nmx, price[u] + child[j].first)
                nmn = minOf(nmn, price[u] + child[j].second)
            }
            nmx = maxOf(nmx, price[u] + upmx)
            nmn = minOf(nmn, price[u] + upmn)
            reroot(v, u, nmx - price[v], nmn - price[v])
            idx++
        }
    }
    fun maxOutput(n: Int, edges: Array<IntArray>, price_: IntArray): Int {
        g = Array(n) { mutableListOf() }
        price = price_
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        dfs(0, -1)
        reroot(0, -1, 0, 0)
        return ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


class Solution:
    def maxOutput(self, n: int, edges: list[list[int]], price: list[int]) -> int:
        from collections import defaultdict
        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        def dfs(u: int, p: int) -> tuple[int, int]:
            mx = mn = price[u]
            for v in g[u]:
                if v == p:
                    continue
                cmx, cmn = dfs(v, u)
                mx = max(mx, price[u] + cmx)
                mn = min(mn, price[u] + cmn)
            return mx, mn
        def reroot(u: int, p: int, upmx: int, upmn: int):
            nonlocal ans
            mx = mn = price[u]
            child = []
            for v in g[u]:
                if v == p:
                    continue
                cmx, cmn = dfs(v, u)
                child.append((cmx, cmn))
                mx = max(mx, price[u] + cmx)
                mn = min(mn, price[u] + cmn)
            mx = max(mx, price[u] + upmx)
            mn = min(mn, price[u] + upmn)
            ans = max(ans, mx - mn)
            idx = 0
            for v in g[u]:
                if v == p:
                    continue
                nmx = nmn = price[u]
                for j, (cmx, cmn) in enumerate(child):
                    if j == idx:
                        continue
                    nmx = max(nmx, price[u] + cmx)
                    nmn = min(nmn, price[u] + cmn)
                nmx = max(nmx, price[u] + upmx)
                nmn = min(nmn, price[u] + upmn)
                reroot(v, u, nmx - price[v], nmn - price[v])
                idx += 1
        dfs(0, -1)
        reroot(0, -1, 0, 0)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61


impl Solution {
    pub fn max_output(n: i32, edges: Vec<Vec<i32>>, price: Vec<i32>) -> i32 {
        use std::collections::HashMap;
        let mut g = HashMap::new();
        for e in &edges {
            g.entry(e[0]).or_insert(vec![]).push(e[1]);
            g.entry(e[1]).or_insert(vec![]).push(e[0]);
        }
        let mut ans = 0;
        fn dfs(u: i32, p: i32, g: &HashMap<i32, Vec<i32>>, price: &Vec<i32>) -> (i32, i32) {
            let mut mx = price[u as usize];
            let mut mn = price[u as usize];
            if let Some(children) = g.get(&u) {
                for &v in children {
                    if v == p { continue; }
                    let (cmx, cmn) = dfs(v, u, g, price);
                    mx = mx.max(price[u as usize] + cmx);
                    mn = mn.min(price[u as usize] + cmn);
                }
            }
            (mx, mn)
        }
        fn reroot(u: i32, p: i32, upmx: i32, upmn: i32, g: &HashMap<i32, Vec<i32>>, price: &Vec<i32>, ans: &mut i32) {
            let mut mx = price[u as usize];
            let mut mn = price[u as usize];
            let mut child = vec![];
            if let Some(children) = g.get(&u) {
                for &v in children {
                    if v == p { continue; }
                    let (cmx, cmn) = dfs(v, u, g, price);
                    child.push((cmx, cmn));
                    mx = mx.max(price[u as usize] + cmx);
                    mn = mn.min(price[u as usize] + cmn);
                }
            }
            mx = mx.max(price[u as usize] + upmx);
            mn = mn.min(price[u as usize] + upmn);
            *ans = (*ans).max(mx - mn);
            let mut idx = 0;
            if let Some(children) = g.get(&u) {
                for &v in children {
                    if v == p { continue; }
                    let mut nmx = price[u as usize];
                    let mut nmn = price[u as usize];
                    for (j, (cmx, cmn)) in child.iter().enumerate() {
                        if j == idx { continue; }
                        nmx = nmx.max(price[u as usize] + cmx);
                        nmn = nmn.min(price[u as usize] + cmn);
                    }
                    nmx = nmx.max(price[u as usize] + upmx);
                    nmn = nmn.min(price[u as usize] + upmn);
                    reroot(v, u, nmx - price[v as usize], nmn - price[v as usize], g, price, ans);
                    idx += 1;
                }
            }
        }
        dfs(0, -1, &g, &price);
        reroot(0, -1, 0, 0, &g, &price, &mut ans);
        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51


class Solution {
    maxOutput(n: number, edges: number[][], price: number[]): number {
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [a, b] of edges) {
            g[a].push(b);
            g[b].push(a);
        }
        let ans = 0;
        function dfs(u: number, p: number): [number, number] {
            let mx = price[u], mn = price[u];
            for (const v of g[u]) {
                if (v === p) continue;
                const [cmx, cmn] = dfs(v, u);
                mx = Math.max(mx, price[u] + cmx);
                mn = Math.min(mn, price[u] + cmn);
            }
            return [mx, mn];
        }
        function reroot(u: number, p: number, upmx: number, upmn: number) {
            let mx = price[u], mn = price[u];
            const child: [number, number][] = [];
            for (const v of g[u]) {
                if (v === p) continue;
                const [cmx, cmn] = dfs(v, u);
                child.push([cmx, cmn]);
                mx = Math.max(mx, price[u] + cmx);
                mn = Math.min(mn, price[u] + cmn);
            }
            mx = Math.max(mx, price[u] + upmx);
            mn = Math.min(mn, price[u] + upmn);
            ans = Math.max(ans, mx - mn);
            let idx = 0;
            for (const v of g[u]) {
                if (v === p) continue;
                let nmx = price[u], nmn = price[u];
                for (let j = 0; j < child.length; ++j) {
                    if (j === idx) continue;
                    nmx = Math.max(nmx, price[u] + child[j][0]);
                    nmn = Math.min(nmn, price[u] + child[j][1]);
                }
                nmx = Math.max(nmx, price[u] + upmx);
                nmn = Math.min(nmn, price[u] + upmn);
                reroot(v, u, nmx - price[v], nmn - price[v]);
                idx++;
            }
        }
        dfs(0, -1);
        reroot(0, -1, 0, 0);
        return ans;
    }
}

Complexity

⏰ Time complexity: O(n), since each node and edge is visited a constant number of times.
🧺 Space complexity: O(n), for the adjacency list and recursion stack.

Problem#

Examples#

Example 1#

Example 2#

Constraints#

Solution#

Method 1 – Rerooting DP (Dynamic Programming on Trees)#

Intuition#

Approach#

Code#

Complexity#