problemmediumalgorithmsleetcode-2482leetcode 2482leetcode2482

Difference Between Ones and Zeros in Row and Column

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a 0-indexed m x n binary matrix grid.

A 0-indexed m x n difference matrix diff is created with the following procedure:

  • Let the number of ones in the ith row be onesRowi.
  • Let the number of ones in the jth column be onesColj.
  • Let the number of zeros in the ith row be zerosRowi.
  • Let the number of zeros in the jth column be zerosColj.
  • diff[i][j] = onesRowi + onesColj - zerosRowi - zerosColj

Return the difference matrixdiff.

Examples

Example 1


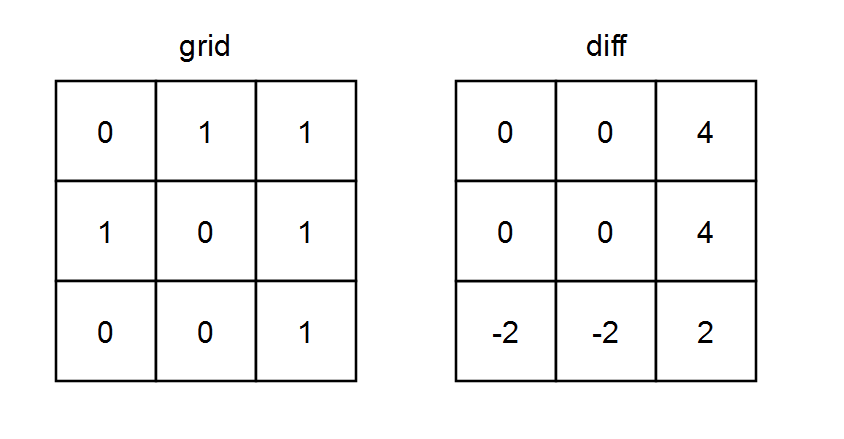
![](https://assets.leetcode.com/uploads/2022/11/06/image-20221106171729-5.png)

Input: grid = [[0,1,1],[1,0,1],[0,0,1]]
Output: [[0,0,4],[0,0,4],[-2,-2,2]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 2 + 1 - 1 - 2 = 0 
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 2 + 1 - 1 - 2 = 0 
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 2 + 3 - 1 - 0 = 4 
- diff[2][0] = onesRow2 + onesCol0 - zerosRow2 - zerosCol0 = 1 + 1 - 2 - 2 = -2
- diff[2][1] = onesRow2 + onesCol1 - zerosRow2 - zerosCol1 = 1 + 1 - 2 - 2 = -2
- diff[2][2] = onesRow2 + onesCol2 - zerosRow2 - zerosCol2 = 1 + 3 - 2 - 0 = 2

Example 2


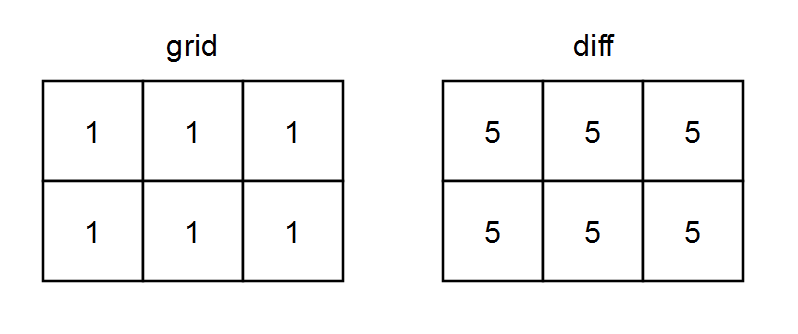
![](https://assets.leetcode.com/uploads/2022/11/06/image-20221106171747-6.png)

Input: grid = [[1,1,1],[1,1,1]]
Output: [[5,5,5],[5,5,5]]
Explanation:
- diff[0][0] = onesRow0 + onesCol0 - zerosRow0 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[0][1] = onesRow0 + onesCol1 - zerosRow0 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[0][2] = onesRow0 + onesCol2 - zerosRow0 - zerosCol2 = 3 + 2 - 0 - 0 = 5
- diff[1][0] = onesRow1 + onesCol0 - zerosRow1 - zerosCol0 = 3 + 2 - 0 - 0 = 5
- diff[1][1] = onesRow1 + onesCol1 - zerosRow1 - zerosCol1 = 3 + 2 - 0 - 0 = 5
- diff[1][2] = onesRow1 + onesCol2 - zerosRow1 - zerosCol2 = 3 + 2 - 0 - 0 = 5

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 1 <= m * n <= 10^5
  • grid[i][j] is either 0 or 1.

Solution

Method 1 – Precompute Row and Column Counts

Intuition

For each cell, we need the number of ones and zeros in its row and column. We can precompute these counts for all rows and columns, then use them to fill the diff matrix efficiently.

Approach

  1. For each row, count the number of ones and zeros.
  2. For each column, count the number of ones and zeros.
  3. For each cell (i, j), compute:
    • diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j]
  4. Return the diff matrix.

Code

C++
class Solution {
public:
    vector<vector<int>> onesMinusZeros(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<int> onesRow(m), zerosRow(m), onesCol(n), zerosCol(n);
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) onesRow[i]++, onesCol[j]++;
                else zerosRow[i]++, zerosCol[j]++;
            }
        vector<vector<int>> diff(m, vector<int>(n));
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j];
        return diff;
    }
};
Go
func onesMinusZeros(grid [][]int) [][]int {
    m, n := len(grid), len(grid[0])
    onesRow, zerosRow := make([]int, m), make([]int, m)
    onesCol, zerosCol := make([]int, n), make([]int, n)
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == 1 {
                onesRow[i]++
                onesCol[j]++
            } else {
                zerosRow[i]++
                zerosCol[j]++
            }
        }
    }
    diff := make([][]int, m)
    for i := 0; i < m; i++ {
        diff[i] = make([]int, n)
        for j := 0; j < n; j++ {
            diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j]
        }
    }
    return diff
}
Java
class Solution {
    public int[][] onesMinusZeros(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[] onesRow = new int[m], zerosRow = new int[m], onesCol = new int[n], zerosCol = new int[n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                if (grid[i][j] == 1) { onesRow[i]++; onesCol[j]++; }
                else { zerosRow[i]++; zerosCol[j]++; }
        int[][] diff = new int[m][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j];
        return diff;
    }
}
Kotlin
class Solution {
    fun onesMinusZeros(grid: Array<IntArray>): Array<IntArray> {
        val m = grid.size
        val n = grid[0].size
        val onesRow = IntArray(m)
        val zerosRow = IntArray(m)
        val onesCol = IntArray(n)
        val zerosCol = IntArray(n)
        for (i in 0 until m)
            for (j in 0 until n)
                if (grid[i][j] == 1) { onesRow[i]++; onesCol[j]++ }
                else { zerosRow[i]++; zerosCol[j]++ }
        val diff = Array(m) { IntArray(n) }
        for (i in 0 until m)
            for (j in 0 until n)
                diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j]
        return diff
    }
}
Python
class Solution:
    def onesMinusZeros(self, grid: list[list[int]]) -> list[list[int]]:
        m, n = len(grid), len(grid[0])
        ones_row = [sum(row) for row in grid]
        zeros_row = [n - x for x in ones_row]
        ones_col = [sum(grid[i][j] for i in range(m)) for j in range(n)]
        zeros_col = [m - x for x in ones_col]
        diff = [[ones_row[i] + ones_col[j] - zeros_row[i] - zeros_col[j] for j in range(n)] for i in range(m)]
        return diff
Rust
impl Solution {
    pub fn ones_minus_zeros(grid: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = grid.len();
        let n = grid[0].len();
        let mut ones_row = vec![0; m];
        let mut zeros_row = vec![0; m];
        let mut ones_col = vec![0; n];
        let mut zeros_col = vec![0; n];
        for i in 0..m {
            for j in 0..n {
                if grid[i][j] == 1 {
                    ones_row[i] += 1;
                    ones_col[j] += 1;
                } else {
                    zeros_row[i] += 1;
                    zeros_col[j] += 1;
                }
            }
        }
        let mut diff = vec![vec![0; n]; m];
        for i in 0..m {
            for j in 0..n {
                diff[i][j] = ones_row[i] + ones_col[j] - zeros_row[i] - zeros_col[j];
            }
        }
        diff
    }
}
TypeScript
class Solution {
    onesMinusZeros(grid: number[][]): number[][] {
        const m = grid.length, n = grid[0].length;
        const onesRow = grid.map(row => row.reduce((a, b) => a + b, 0));
        const zerosRow = onesRow.map(x => n - x);
        const onesCol = Array(n).fill(0);
        for (let j = 0; j < n; ++j)
            for (let i = 0; i < m; ++i)
                onesCol[j] += grid[i][j];
        const zerosCol = onesCol.map(x => m - x);
        const diff = Array.from({length: m}, () => Array(n).fill(0));
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                diff[i][j] = onesRow[i] + onesCol[j] - zerosRow[i] - zerosCol[j];
        return diff;
    }
}

Complexity

  • ⏰ Time complexity: O(m * n), as we scan the grid and fill the diff matrix.
  • 🧺 Space complexity: O(m + n), for storing row and column counts.

Comments