Difference of Number of Distinct Values on Diagonals

Problem

Given a 2D grid of size m x n, you should find the matrix answer of size m x n.

The cell answer[r][c] is calculated by looking at the diagonal values of the cell grid[r][c]:

• Let leftAbove[r][c] be the number of distinct values on the diagonal to the left and above the cell grid[r][c] not including the cell grid[r][c] itself.
• Let rightBelow[r][c] be the number of distinct values on the diagonal to the right and below the cell grid[r][c], not including the cell grid[r][c] itself.
• Then answer[r][c] = |leftAbove[r][c] - rightBelow[r][c]|.

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until the end of the matrix is reached.

• For example, in the below diagram the diagonal is highlighted using the cell with indices (2, 3) colored gray:
• Red-colored cells are left and above the cell.
• Blue-colored cells are right and below the cell.

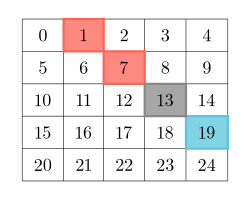
Return the matrix answer.

Examples

Example 1

Input: grid = [[1,2,3],[3,1,5],[3,2,1]]

Output: Output: [[1,1,0],[1,0,1],[0,1,1]]

Explanation:

To calculate the `answer` cells:

answer | left-above elements | leftAbove | right-below elements | rightBelow | |leftAbove - rightBelow|  
---|---|---|---|---|---  
[0][0] | [] | 0 | [grid[1][1], grid[2][2]] | |{1, 1}| = 1 | 1  
[0][1] | [] | 0 | [grid[1][2]] | |{5}| = 1 | 1  
[0][2] | [] | 0 | [] | 0 | 0  
[1][0] | [] | 0 | [grid[2][1]] | |{2}| = 1 | 1  
[1][1] | [grid[0][0]] | |{1}| = 1 | [grid[2][2]] | |{1}| = 1 | 0  
[1][2] | [grid[0][1]] | |{2}| = 1 | [] | 0 | 1  
[2][0] | [] | 0 | [] | 0 | 0  
[2][1] | [grid[1][0]] | |{3}| = 1 | [] | 0 | 1  
[2][2] | [grid[0][0], grid[1][1]] | |{1, 1}| = 1 | [] | 0 | 1  
  

Example 2

Input: grid = [[1]]

Output: Output: [[0]]

Constraints

• m == grid.length
• n == grid[i].length
• 1 <= m, n, grid[i][j] <= 50

Solution

Method 1 – Diagonal Hash Sets

Intuition

For each cell, the diagonal to the left and above is all cells (r-1, c-1), (r-2, c-2), ... and the diagonal to the right and below is all cells (r+1, c+1), (r+2, c+2), ... We can precompute the distinct values for each diagonal in both directions using hash sets.

Approach

1. For each diagonal (r-c is constant), traverse from top-left to bottom-right, collecting distinct values for left-above for each cell.
2. For each diagonal, traverse from bottom-right to top-left, collecting distinct values for right-below for each cell.
3. For each cell, answer[r][c] = |leftAbove[r][c] - rightBelow[r][c]|.

Code

C++

class Solution {
public:
    vector<vector<int>> differenceOfDistinctValues(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> left(m, vector<int>(n)), right(m, vector<int>(n));
        // Left-above
        for (int d = -(n-1); d <= m-1; ++d) {
            unordered_set<int> s;
            for (int i = max(0, d), j = i - d; i < m && j < n; ++i, ++j) {
                left[i][j] = s.size();
                s.insert(grid[i][j]);
            }
        }
        // Right-below
        for (int d = -(n-1); d <= m-1; ++d) {
            unordered_set<int> s;
            vector<pair<int,int>> cells;
            for (int i = max(0, d), j = i - d; i < m && j < n; ++i, ++j)
                cells.push_back({i, j});
            for (int k = (int)cells.size()-1; k >= 0; --k) {
                int i = cells[k].first, j = cells[k].second;
                right[i][j] = s.size();
                s.insert(grid[i][j]);
            }
        }
        vector<vector<int>> ans(m, vector<int>(n));
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                ans[i][j] = abs(left[i][j] - right[i][j]);
        return ans;
    }
};

Go

func differenceOfDistinctValues(grid [][]int) [][]int {
    m, n := len(grid), len(grid[0])
    left := make([][]int, m)
    right := make([][]int, m)
    for i := range left {
        left[i] = make([]int, n)
        right[i] = make([]int, n)
    }
    for d := -(n-1); d <= m-1; d++ {
        s := map[int]struct{}{}
        for i, j := max(0, d), max(0, -d); i < m && j < n; i, j = i+1, j+1 {
            left[i][j] = len(s)
            s[grid[i][j]] = struct{}{}
        }
    }
    for d := -(n-1); d <= m-1; d++ {
        s := map[int]struct{}{}
        cells := [][2]int{}
        for i, j := max(0, d), max(0, -d); i < m && j < n; i, j = i+1, j+1 {
            cells = append(cells, [2]int{i, j})
        }
        for k := len(cells)-1; k >= 0; k-- {
            i, j := cells[k][0], cells[k][1]
            right[i][j] = len(s)
            s[grid[i][j]] = struct{}{}
        }
    }
    ans := make([][]int, m)
    for i := range ans {
        ans[i] = make([]int, n)
        for j := 0; j < n; j++ {
            ans[i][j] = abs(left[i][j] - right[i][j])
        }
    }
    return ans
}
func max(a, b int) int { if a > b { return a }; return b }
func abs(x int) int { if x < 0 { return -x }; return x }

Java

class Solution {
    public int[][] differenceOfDistinctValues(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int[][] left = new int[m][n], right = new int[m][n];
        for (int d = -(n-1); d <= m-1; ++d) {
            Set<Integer> s = new HashSet<>();
            for (int i = Math.max(0, d), j = i - d; i < m && j < n; ++i, ++j) {
                left[i][j] = s.size();
                s.add(grid[i][j]);
            }
        }
        for (int d = -(n-1); d <= m-1; ++d) {
            Set<Integer> s = new HashSet<>();
            List<int[]> cells = new ArrayList<>();
            for (int i = Math.max(0, d), j = i - d; i < m && j < n; ++i, ++j)
                cells.add(new int[]{i, j});
            for (int k = cells.size()-1; k >= 0; --k) {
                int i = cells.get(k)[0], j = cells.get(k)[1];
                right[i][j] = s.size();
                s.add(grid[i][j]);
            }
        }
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                ans[i][j] = Math.abs(left[i][j] - right[i][j]);
        return ans;
    }
}

Kotlin

class Solution {
    fun differenceOfDistinctValues(grid: Array<IntArray>): Array<IntArray> {
        val m = grid.size
        val n = grid[0].size
        val left = Array(m) { IntArray(n) }
        val right = Array(m) { IntArray(n) }
        for (d in -(n-1)..(m-1)) {
            val s = mutableSetOf<Int>()
            var i = maxOf(0, d)
            var j = i - d
            while (i < m && j < n) {
                left[i][j] = s.size
                s.add(grid[i][j])
                i++
                j++
            }
        }
        for (d in -(n-1)..(m-1)) {
            val s = mutableSetOf<Int>()
            val cells = mutableListOf<Pair<Int, Int>>()
            var i = maxOf(0, d)
            var j = i - d
            while (i < m && j < n) {
                cells.add(i to j)
                i++
                j++
            }
            for (k in cells.size-1 downTo 0) {
                val (ii, jj) = cells[k]
                right[ii][jj] = s.size
                s.add(grid[ii][jj])
            }
        }
        val ans = Array(m) { IntArray(n) }
        for (i in 0 until m)
            for (j in 0 until n)
                ans[i][j] = kotlin.math.abs(left[i][j] - right[i][j])
        return ans
    }
}

Python

class Solution:
    def differenceOfDistinctValues(self, grid: list[list[int]]) -> list[list[int]]:
        m, n = len(grid), len(grid[0])
        left = [[0]*n for _ in range(m)]
        right = [[0]*n for _ in range(m)]
        for d in range(-(n-1), m):
            s = set()
            i, j = max(0, d), max(0, -d)
            while i < m and j < n:
                left[i][j] = len(s)
                s.add(grid[i][j])
                i += 1
                j += 1
        for d in range(-(n-1), m):
            s = set()
            cells = []
            i, j = max(0, d), max(0, -d)
            while i < m and j < n:
                cells.append((i, j))
                i += 1
                j += 1
            for i, j in reversed(cells):
                right[i][j] = len(s)
                s.add(grid[i][j])
        ans = [[abs(left[i][j] - right[i][j]) for j in range(n)] for i in range(m)]
        return ans

Rust

impl Solution {
    pub fn difference_of_distinct_values(grid: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = grid.len();
        let n = grid[0].len();
        let mut left = vec![vec![0; n]; m];
        let mut right = vec![vec![0; n]; m];
        for d in -(n as isize - 1)..=(m as isize - 1) {
            let mut s = std::collections::HashSet::new();
            let mut i = std::cmp::max(0, d) as usize;
            let mut j = (i as isize - d) as usize;
            while i < m && j < n {
                left[i][j] = s.len() as i32;
                s.insert(grid[i][j]);
                i += 1;
                j += 1;
            }
        }
        for d in -(n as isize - 1)..=(m as isize - 1) {
            let mut s = std::collections::HashSet::new();
            let mut cells = vec![];
            let mut i = std::cmp::max(0, d) as usize;
            let mut j = (i as isize - d) as usize;
            while i < m && j < n {
                cells.push((i, j));
                i += 1;
                j += 1;
            }
            for &(i, j) in cells.iter().rev() {
                right[i][j] = s.len() as i32;
                s.insert(grid[i][j]);
            }
        }
        let mut ans = vec![vec![0; n]; m];
        for i in 0..m {
            for j in 0..n {
                ans[i][j] = (left[i][j] - right[i][j]).abs();
            }
        }
        ans
    }
}

TypeScript

class Solution {
    differenceOfDistinctValues(grid: number[][]): number[][] {
        const m = grid.length, n = grid[0].length;
        const left = Array.from({length: m}, () => Array(n).fill(0));
        const right = Array.from({length: m}, () => Array(n).fill(0));
        for (let d = -(n-1); d <= m-1; ++d) {
            const s = new Set<number>();
            for (let i = Math.max(0, d), j = i - d; i < m && j < n; ++i, ++j) {
                left[i][j] = s.size;
                s.add(grid[i][j]);
            }
        }
        for (let d = -(n-1); d <= m-1; ++d) {
            const s = new Set<number>();
            const cells: [number, number][] = [];
            for (let i = Math.max(0, d), j = i - d; i < m && j < n; ++i, ++j)
                cells.push([i, j]);
            for (let k = cells.length-1; k >= 0; --k) {
                const [i, j] = cells[k];
                right[i][j] = s.size;
                s.add(grid[i][j]);
            }
        }
        const ans = Array.from({length: m}, () => Array(n).fill(0));
        for (let i = 0; i < m; ++i)
            for (let j = 0; j < n; ++j)
                ans[i][j] = Math.abs(left[i][j] - right[i][j]);
        return ans;
    }
}

Complexity

• ⏰ Time complexity: O(m * n), as each cell is visited a constant number of times.
• 🧺 Space complexity: O(m * n), for the auxiliary matrices.