problemmediumalgorithmsleetcode-2556leetcode 2556leetcode2556

Disconnect Path in a Binary Matrix by at Most One Flip

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).

You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).

Return true if it is possible to make the matrix disconnect orfalse otherwise.

Note that flipping a cell changes its value from 0 to 1 or from 1 to 0.

Examples

Example 1


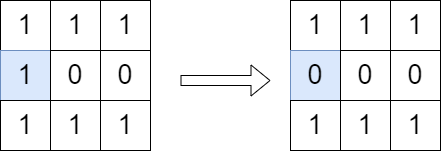
![](https://assets.leetcode.com/uploads/2022/12/07/yetgrid2drawio.png)

Input: grid = [[1,1,1],[1,0,0],[1,1,1]]
Output: true
Explanation: We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.

Example 2


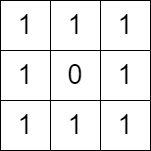
![](https://assets.leetcode.com/uploads/2022/12/07/yetgrid3drawio.png)

Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: false
Explanation: It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).

Constraints

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 1000
  • 1 <= m * n <= 10^5
  • grid[i][j] is either 0 or 1.
  • grid[0][0] == grid[m - 1][n - 1] == 1

Solution

Method 1 – Path Uniqueness Check (DFS or Greedy)

Intuition

If there is only one unique path from (0,0) to (m-1,n-1), then flipping any cell (except the endpoints) on that path will disconnect the matrix. If there are two or more disjoint paths, then no single flip can disconnect the matrix. So, check if there is more than one path.

Approach

  1. Use DFS or greedy to find the first path from (0,0) to (m-1,n-1), marking the path.
  2. Try to find a second path from (0,0) to (m-1,n-1) that does not reuse the first path's cells (except endpoints).
  3. If a second path exists, return False. Otherwise, return True.

Code

C++
class Solution {
public:
    bool isPossibleToCutPath(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        function<bool(int,int)> dfs = [&](int x, int y) {
            if (x < 0 || y < 0 || x >= m || y >= n || grid[x][y] == 0) return false;
            if (x == m-1 && y == n-1) return true;
            grid[x][y] = 0;
            return dfs(x+1, y) || dfs(x, y+1);
        };
        dfs(0, 0);
        return !dfs(0, 0);
    }
};
Go
func isPossibleToCutPath(grid [][]int) bool {
    m, n := len(grid), len(grid[0])
    var dfs func(x, y int) bool
    dfs = func(x, y int) bool {
        if x < 0 || y < 0 || x >= m || y >= n || grid[x][y] == 0 {
            return false
        }
        if x == m-1 && y == n-1 {
            return true
        }
        grid[x][y] = 0
        return dfs(x+1, y) || dfs(x, y+1)
    }
    dfs(0, 0)
    return !dfs(0, 0)
}
Java
class Solution {
    public boolean isPossibleToCutPath(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        if (!dfs(grid, 0, 0, m, n)) return true;
        return !dfs(grid, 0, 0, m, n);
    }
    private boolean dfs(int[][] grid, int x, int y, int m, int n) {
        if (x < 0 || y < 0 || x >= m || y >= n || grid[x][y] == 0) return false;
        if (x == m-1 && y == n-1) return true;
        grid[x][y] = 0;
        boolean res = dfs(grid, x+1, y, m, n) || dfs(grid, x, y+1, m, n);
        return res;
    }
}
Kotlin
class Solution {
    fun isPossibleToCutPath(grid: Array<IntArray>): Boolean {
        val m = grid.size
        val n = grid[0].size
        fun dfs(x: Int, y: Int): Boolean {
            if (x !in 0 until m || y !in 0 until n || grid[x][y] == 0) return false
            if (x == m-1 && y == n-1) return true
            grid[x][y] = 0
            return dfs(x+1, y) || dfs(x, y+1)
        }
        dfs(0, 0)
        return !dfs(0, 0)
    }
}
Python
class Solution:
    def isPossibleToCutPath(self, grid: list[list[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        def dfs(x: int, y: int) -> bool:
            if x < 0 or y < 0 or x >= m or y >= n or grid[x][y] == 0:
                return False
            if x == m-1 and y == n-1:
                return True
            grid[x][y] = 0
            return dfs(x+1, y) or dfs(x, y+1)
        dfs(0, 0)
        return not dfs(0, 0)
Rust
impl Solution {
    pub fn is_possible_to_cut_path(mut grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        fn dfs(grid: &mut Vec<Vec<i32>>, x: usize, y: usize, m: usize, n: usize) -> bool {
            if x >= m || y >= n || grid[x][y] == 0 { return false; }
            if x == m-1 && y == n-1 { return true; }
            grid[x][y] = 0;
            dfs(grid, x+1, y, m, n) || dfs(grid, x, y+1, m, n)
        }
        dfs(&mut grid, 0, 0, m, n);
        !dfs(&mut grid, 0, 0, m, n)
    }
}
TypeScript
class Solution {
    isPossibleToCutPath(grid: number[][]): boolean {
        const m = grid.length, n = grid[0].length;
        function dfs(x: number, y: number): boolean {
            if (x < 0 || y < 0 || x >= m || y >= n || grid[x][y] === 0) return false;
            if (x === m-1 && y === n-1) return true;
            grid[x][y] = 0;
            return dfs(x+1, y) || dfs(x, y+1);
        }
        dfs(0, 0);
        return !dfs(0, 0);
    }
}

Complexity

  • ⏰ Time complexity: O(m * n), since each cell is visited at most twice.
  • 🧺 Space complexity: O(m * n), for the recursion stack in the worst case.

Comments