Problem

You are given a positive integer n representing the number of nodes in a connected undirected graph containing exactly one cycle. The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [node1i, node2i] denotes that there is a bidirectional edge connecting node1i and node2i in the graph.

The distance between two nodes a and b is defined to be the minimum number of edges that are needed to go from a to b.

Return an integer arrayanswer of sizen , whereanswer[i]_is theminimum distance between the _ith node andany node in the cycle.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2204.Distance%20to%20a%20Cycle%20in%20Undirected%20Graph/images/image-20220315154238-1.png)
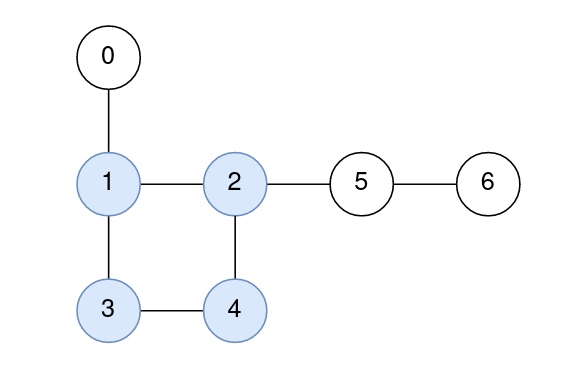
Input: n = 7, edges = [[1,2],[2,4],[4,3],[3,1],[0,1],[5,2],[6,5]]
Output: [1,0,0,0,0,1,2]
Explanation:
The nodes 1, 2, 3, and 4 form the cycle.
The distance from 0 to 1 is 1.
The distance from 1 to 1 is 0.
The distance from 2 to 2 is 0.
The distance from 3 to 3 is 0.
The distance from 4 to 4 is 0.
The distance from 5 to 2 is 1.
The distance from 6 to 2 is 2.

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/2200-2299/2204.Distance%20to%20a%20Cycle%20in%20Undirected%20Graph/images/image-20220315154634-1.png)
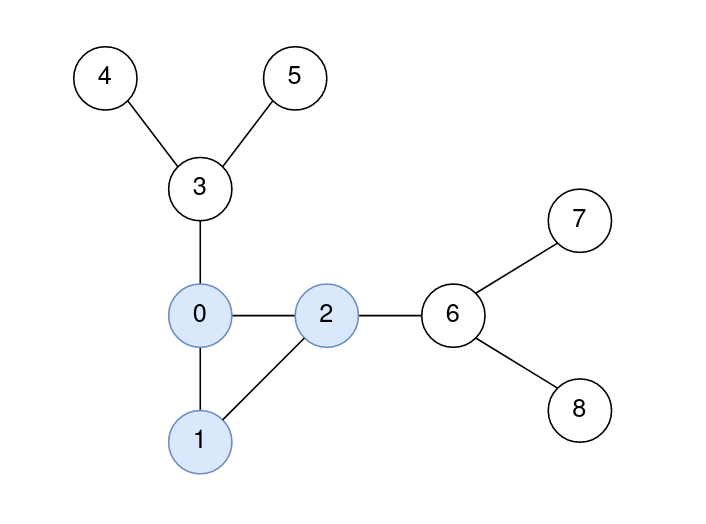
Input: n = 9, edges = [[0,1],[1,2],[0,2],[2,6],[6,7],[6,8],[0,3],[3,4],[3,5]]
Output: [0,0,0,1,2,2,1,2,2]
Explanation:
The nodes 0, 1, and 2 form the cycle.
The distance from 0 to 0 is 0.
The distance from 1 to 1 is 0.
The distance from 2 to 2 is 0.
The distance from 3 to 1 is 1.
The distance from 4 to 1 is 2.
The distance from 5 to 1 is 2.
The distance from 6 to 2 is 1.
The distance from 7 to 2 is 2.
The distance from 8 to 2 is 2.

Constraints:

  • 3 <= n <= 10^5
  • edges.length == n
  • edges[i].length == 2
  • 0 <= node1i, node2i <= n - 1
  • node1i != node2i
  • The graph is connected.
  • The graph has exactly one cycle.
  • There is at most one edge between any pair of vertices.

Solution

Method 1 – Cycle Detection and BFS

Intuition

The graph has exactly one cycle. If we can find all nodes in the cycle, then for every node, the minimum distance to the cycle is the shortest path to any node in the cycle. We can use DFS to find the cycle, then BFS from all cycle nodes to compute distances.

Approach

  1. Build the adjacency list for the graph.
  2. Use DFS to find and mark all nodes in the cycle:
    • Track the parent of each node to avoid trivial cycles.
    • When a back edge is found, record the cycle path.
  3. Use BFS starting from all cycle nodes to compute the minimum distance for every node to the cycle.
  4. Return the distance array.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

class Solution {
public:
    vector<int> distanceToCycle(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        vector<int> inCycle(n, 0), parent(n, -1);
        int start = -1, end = -1;
        function<bool(int, int)> dfs = [&](int u, int p) {
            parent[u] = p;
            for (int v : g[u]) {
                if (v == p) continue;
                if (parent[v] == -1) {
                    if (dfs(v, u)) return true;
                } else {
                    start = v; end = u;
                    return true;
                }
            }
            return false;
        };
        dfs(0, -1);
        vector<int> cycle;
        int x = end;
        while (x != start) {
            inCycle[x] = 1;
            cycle.push_back(x);
            x = parent[x];
        }
        inCycle[start] = 1;
        cycle.push_back(start);
        vector<int> ans(n, -1);
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            if (inCycle[i]) {
                ans[i] = 0;
                q.push(i);
            }
        }
        while (!q.empty()) {
            int u = q.front(); q.pop();
            for (int v : g[u]) {
                if (ans[v] == -1) {
                    ans[v] = ans[u] + 1;
                    q.push(v);
                }
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

func distanceToCycle(n int, edges [][]int) []int {
    g := make([][]int, n)
    for _, e := range edges {
        g[e[0]] = append(g[e[0]], e[1])
        g[e[1]] = append(g[e[1]], e[0])
    }
    inCycle := make([]bool, n)
    parent := make([]int, n)
    for i := range parent { parent[i] = -1 }
    var start, end int
    var found bool
    var dfs func(u, p int) bool
    dfs = func(u, p int) bool {
        parent[u] = p
        for _, v := range g[u] {
            if v == p { continue }
            if parent[v] == -1 {
                if dfs(v, u) { return true }
            } else {
                start, end = v, u
                return true
            }
        }
        return false
    }
    dfs(0, -1)
    x := end
    for x != start {
        inCycle[x] = true
        x = parent[x]
    }
    inCycle[start] = true
    ans := make([]int, n)
    for i := range ans { ans[i] = -1 }
    q := []int{}
    for i := 0; i < n; i++ {
        if inCycle[i] {
            ans[i] = 0
            q = append(q, i)
        }
    }
    for len(q) > 0 {
        u := q[0]; q = q[1:]
        for _, v := range g[u] {
            if ans[v] == -1 {
                ans[v] = ans[u] + 1
                q = append(q, v)
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

class Solution {
    public int[] distanceToCycle(int n, int[][] edges) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i < n; ++i) g.add(new ArrayList<>());
        for (int[] e : edges) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        int[] inCycle = new int[n], parent = new int[n];
        Arrays.fill(parent, -1);
        int start = -1, end = -1;
        boolean[] found = new boolean[1];
        dfs(0, -1, g, parent, found, new int[]{-1, -1});
        start = found[0] ? found[1] : -1;
        end = found[0] ? found[2] : -1;
        List<Integer> cycle = new ArrayList<>();
        int x = end;
        while (x != start) {
            inCycle[x] = 1;
            cycle.add(x);
            x = parent[x];
        }
        inCycle[start] = 1;
        cycle.add(start);
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        Queue<Integer> q = new LinkedList<>();
        for (int i = 0; i < n; ++i) {
            if (inCycle[i] == 1) {
                ans[i] = 0;
                q.offer(i);
            }
        }
        while (!q.isEmpty()) {
            int u = q.poll();
            for (int v : g.get(u)) {
                if (ans[v] == -1) {
                    ans[v] = ans[u] + 1;
                    q.offer(v);
                }
            }
        }
        return ans;
    }
    private boolean dfs(int u, int p, List<List<Integer>> g, int[] parent, boolean[] found, int[] se) {
        parent[u] = p;
        for (int v : g.get(u)) {
            if (v == p) continue;
            if (parent[v] == -1) {
                if (dfs(v, u, g, parent, found, se)) return true;
            } else {
                found[0] = true; se[1] = v; se[2] = u;
                return true;
            }
        }
        return false;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

class Solution {
    fun distanceToCycle(n: Int, edges: Array<IntArray>): IntArray {
        val g = Array(n) { mutableListOf<Int>() }
        for (e in edges) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        val inCycle = BooleanArray(n)
        val parent = IntArray(n) { -1 }
        var start = -1
        var end = -1
        fun dfs(u: Int, p: Int): Boolean {
            parent[u] = p
            for (v in g[u]) {
                if (v == p) continue
                if (parent[v] == -1) {
                    if (dfs(v, u)) return true
                } else {
                    start = v; end = u
                    return true
                }
            }
            return false
        }
        dfs(0, -1)
        var x = end
        while (x != start) {
            inCycle[x] = true
            x = parent[x]
        }
        inCycle[start] = true
        val ans = IntArray(n) { -1 }
        val q = ArrayDeque<Int>()
        for (i in 0 until n) {
            if (inCycle[i]) {
                ans[i] = 0
                q.add(i)
            }
        }
        while (q.isNotEmpty()) {
            val u = q.removeFirst()
            for (v in g[u]) {
                if (ans[v] == -1) {
                    ans[v] = ans[u] + 1
                    q.add(v)
                }
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

class Solution:
    def distanceToCycle(self, n: int, edges: list[list[int]]) -> list[int]:
        g = [[] for _ in range(n)]
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        parent = [-1] * n
        start = end = -1
        def dfs(u, p):
            nonlocal start, end
            parent[u] = p
            for v in g[u]:
                if v == p:
                    continue
                if parent[v] == -1:
                    if dfs(v, u):
                        return True
                else:
                    start, end = v, u
                    return True
            return False
        dfs(0, -1)
        in_cycle = [0] * n
        x = end
        while x != start:
            in_cycle[x] = 1
            x = parent[x]
        in_cycle[start] = 1
        from collections import deque
        ans = [-1] * n
        q = deque()
        for i in range(n):
            if in_cycle[i]:
                ans[i] = 0
                q.append(i)
        while q:
            u = q.popleft()
            for v in g[u]:
                if ans[v] == -1:
                    ans[v] = ans[u] + 1
                    q.append(v)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

impl Solution {
    pub fn distance_to_cycle(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        for e in &edges {
            g[e[0] as usize].push(e[1] as usize);
            g[e[1] as usize].push(e[0] as usize);
        }
        let mut parent = vec![-1; n];
        let (mut start, mut end) = (-1, -1);
        fn dfs(u: usize, p: i32, g: &Vec<Vec<usize>>, parent: &mut Vec<i32>, start: &mut i32, end: &mut i32) -> bool {
            parent[u] = p;
            for &v in &g[u] {
                if v as i32 == p { continue; }
                if parent[v] == -1 {
                    if dfs(v, u as i32, g, parent, start, end) { return true; }
                } else {
                    *start = v as i32; *end = u as i32;
                    return true;
                }
            }
            false
        }
        dfs(0, -1, &g, &mut parent, &mut start, &mut end);
        let mut in_cycle = vec![false; n];
        let mut x = end;
        while x != start {
            in_cycle[x as usize] = true;
            x = parent[x as usize];
        }
        in_cycle[start as usize] = true;
        let mut ans = vec![-1; n];
        let mut q = std::collections::VecDeque::new();
        for i in 0..n {
            if in_cycle[i] {
                ans[i] = 0;
                q.push_back(i);
            }
        }
        while let Some(u) = q.pop_front() {
            for &v in &g[u] {
                if ans[v] == -1 {
                    ans[v] = ans[u] + 1;
                    q.push_back(v);
                }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

class Solution {
    distanceToCycle(n: number, edges: number[][]): number[] {
        const g: number[][] = Array.from({length: n}, () => []);
        for (const [a, b] of edges) {
            g[a].push(b);
            g[b].push(a);
        }
        const parent = Array(n).fill(-1);
        let start = -1, end = -1;
        function dfs(u: number, p: number): boolean {
            parent[u] = p;
            for (const v of g[u]) {
                if (v === p) continue;
                if (parent[v] === -1) {
                    if (dfs(v, u)) return true;
                } else {
                    start = v; end = u;
                    return true;
                }
            }
            return false;
        }
        dfs(0, -1);
        const inCycle = Array(n).fill(false);
        let x = end;
        while (x !== start) {
            inCycle[x] = true;
            x = parent[x];
        }
        inCycle[start] = true;
        const ans = Array(n).fill(-1);
        const q: number[] = [];
        for (let i = 0; i < n; ++i) {
            if (inCycle[i]) {
                ans[i] = 0;
                q.push(i);
            }
        }
        let qi = 0;
        while (qi < q.length) {
            const u = q[qi++];
            for (const v of g[u]) {
                if (ans[v] === -1) {
                    ans[v] = ans[u] + 1;
                    q.push(v);
                }
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), since each node and edge is visited a constant number of times.
  • 🧺 Space complexity: O(n), for the adjacency list, parent array, and BFS queue.